Is 4/10 Equivalent To 2/5
saludintensiva
Sep 20, 2025 · 6 min read
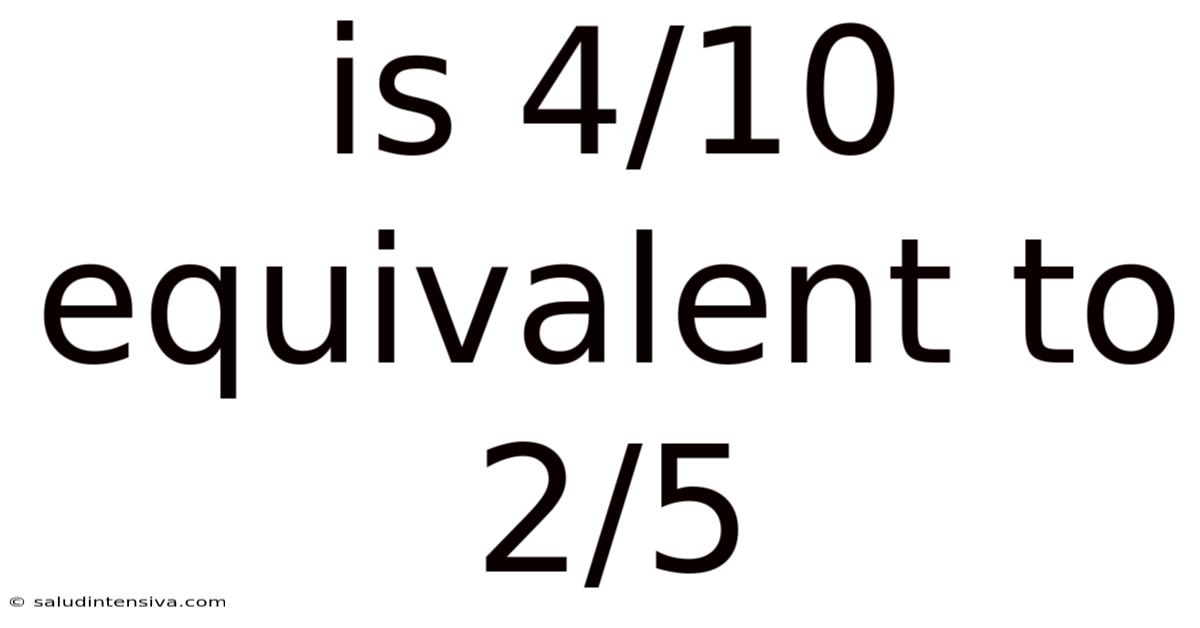
Table of Contents
Is 4/10 Equivalent to 2/5? A Deep Dive into Fraction Equivalence
Are you struggling with fractions? Understanding fraction equivalence is a fundamental skill in mathematics, crucial for everything from baking a cake to calculating complex engineering problems. This comprehensive guide will explore whether 4/10 is equivalent to 2/5, explaining the underlying principles of fraction equivalence and providing practical examples to solidify your understanding. We'll delve into the concept of simplifying fractions, explore different methods for determining equivalence, and address common misconceptions. By the end, you'll confidently tackle fraction equivalence problems and grasp the broader concept of rational numbers.
Understanding Fractions: A Quick Refresher
Before we dive into the equivalence of 4/10 and 2/5, let's quickly review the basics of fractions. A fraction represents a part of a whole. It's composed of two main parts:
- Numerator: The top number, indicating how many parts we have.
- Denominator: The bottom number, indicating the total number of equal parts the whole is divided into.
For example, in the fraction 3/4, the numerator (3) represents three parts, and the denominator (4) signifies that the whole is divided into four equal parts.
Equivalent Fractions: The Same Value, Different Representation
Equivalent fractions represent the same value, even though they look different. Think of it like different ways to express the same amount of money – you can have $1 or four quarters; both represent the same value. Similarly, 1/2, 2/4, 3/6, and so on, all represent the same value – one-half. The key is that the ratio between the numerator and denominator remains constant.
Is 4/10 Equivalent to 2/5? The Proof
Now, let's address the central question: Is 4/10 equivalent to 2/5? The answer is yes. There are several ways to demonstrate this:
Method 1: Simplifying Fractions
Simplifying a fraction means reducing it to its simplest form by dividing both the numerator and the denominator by their greatest common divisor (GCD). The GCD is the largest number that divides both the numerator and denominator without leaving a remainder.
Let's simplify 4/10:
The GCD of 4 and 10 is 2. Dividing both the numerator and denominator by 2 gives us:
4 ÷ 2 / 10 ÷ 2 = 2/5
Therefore, 4/10 simplified is 2/5, proving their equivalence.
Method 2: Finding a Common Denominator
Another way to show equivalence is to find a common denominator for both fractions and compare the numerators. A common denominator is a number that is a multiple of both denominators.
Let's find a common denominator for 4/10 and 2/5:
The denominator of 4/10 is 10, and the denominator of 2/5 is 5. A common denominator is 10 (since 10 is a multiple of 5).
Now, let's convert 2/5 to an equivalent fraction with a denominator of 10:
To change the denominator from 5 to 10, we multiply it by 2. To maintain the same value, we must also multiply the numerator by 2:
2 x 2 / 5 x 2 = 4/10
Since both fractions are now expressed as 4/10, we've proven their equivalence.
Method 3: Cross-Multiplication
Cross-multiplication is a quick way to check if two fractions are equivalent. We multiply the numerator of one fraction by the denominator of the other and vice versa. If the products are equal, the fractions are equivalent.
Let's apply cross-multiplication to 4/10 and 2/5:
4 x 5 = 20
10 x 2 = 20
Since both products are equal (20), we've confirmed that 4/10 and 2/5 are equivalent fractions.
Visual Representation of Equivalence
Imagine you have a pizza cut into 10 slices. Eating 4 slices represents 4/10 of the pizza. Now, imagine the same pizza cut into 5 slices. Eating 2 slices represents 2/5 of the pizza. You've eaten the same amount of pizza in both scenarios, proving the equivalence visually.
Beyond 4/10 and 2/5: Mastering Fraction Equivalence
Understanding the equivalence of 4/10 and 2/5 is a stepping stone to mastering the broader concept of fraction equivalence. Here's a breakdown of how to approach other problems:
-
Identify the GCD: Always begin by finding the greatest common divisor of the numerator and denominator. This simplifies the fraction to its most basic form, making comparisons easier.
-
Prime Factorization: For larger numbers, prime factorization can be helpful in finding the GCD. Break down both the numerator and denominator into their prime factors, and then identify the common factors.
-
Common Denominators: When comparing fractions with different denominators, finding a common denominator is crucial. This allows you to directly compare the numerators. The least common multiple (LCM) of the denominators is often the most efficient common denominator to use.
-
Cross-Multiplication: This method is particularly useful for quickly checking the equivalence of two fractions without simplifying them first.
Common Mistakes to Avoid
-
Adding or Subtracting Numerators and Denominators: Remember, you cannot simply add or subtract the numerators and denominators to determine equivalence. This is a common mistake. You must either simplify the fraction, find a common denominator, or use cross-multiplication.
-
Incorrectly Simplifying Fractions: Ensure you divide both the numerator and denominator by their GCD. Dividing only one by the GCD will change the value of the fraction.
-
Confusing Equivalence with Equality: While equivalent fractions represent the same value, they are not equal in the sense that they are different representations of the same quantity.
Frequently Asked Questions (FAQs)
Q1: Why is simplifying fractions important?
Simplifying fractions makes them easier to work with and understand. It allows for clearer comparisons and simplifies calculations in more complex problems.
Q2: How do I find the greatest common divisor (GCD)?
Several methods exist for finding the GCD, including listing factors, using prime factorization, or employing the Euclidean algorithm (for larger numbers).
Q3: What if the fractions have very large numbers?
For very large numbers, the Euclidean algorithm is the most efficient method for finding the GCD. Calculators or online tools can also assist with these calculations.
Q4: Can I use decimals to check for fraction equivalence?
Yes, you can convert fractions to decimals and compare their decimal values. If the decimal values are identical, the fractions are equivalent.
Conclusion
In conclusion, 4/10 is indeed equivalent to 2/5. This equivalence demonstrates a fundamental principle in mathematics: different fractions can represent the same value. Mastering fraction equivalence is crucial for building a strong foundation in mathematics and tackling more complex mathematical concepts. By understanding the methods of simplifying fractions, finding common denominators, and using cross-multiplication, you can confidently determine the equivalence of any two fractions and excel in your mathematical endeavors. Remember to practice regularly and address any confusion promptly to solidify your understanding. The more you practice, the more intuitive fraction equivalence will become.
Latest Posts
Latest Posts
-
How Many Inches In 3m
Sep 20, 2025
-
Mph To Yards Per Second
Sep 20, 2025
-
How To Find Cost Price
Sep 20, 2025
-
Free Picture Bingo Card Generator
Sep 20, 2025
-
Solving Inequalities With Negative Numbers
Sep 20, 2025
Related Post
Thank you for visiting our website which covers about Is 4/10 Equivalent To 2/5 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.