Is 5/10 Equivalent To 1/2
saludintensiva
Sep 12, 2025 · 5 min read
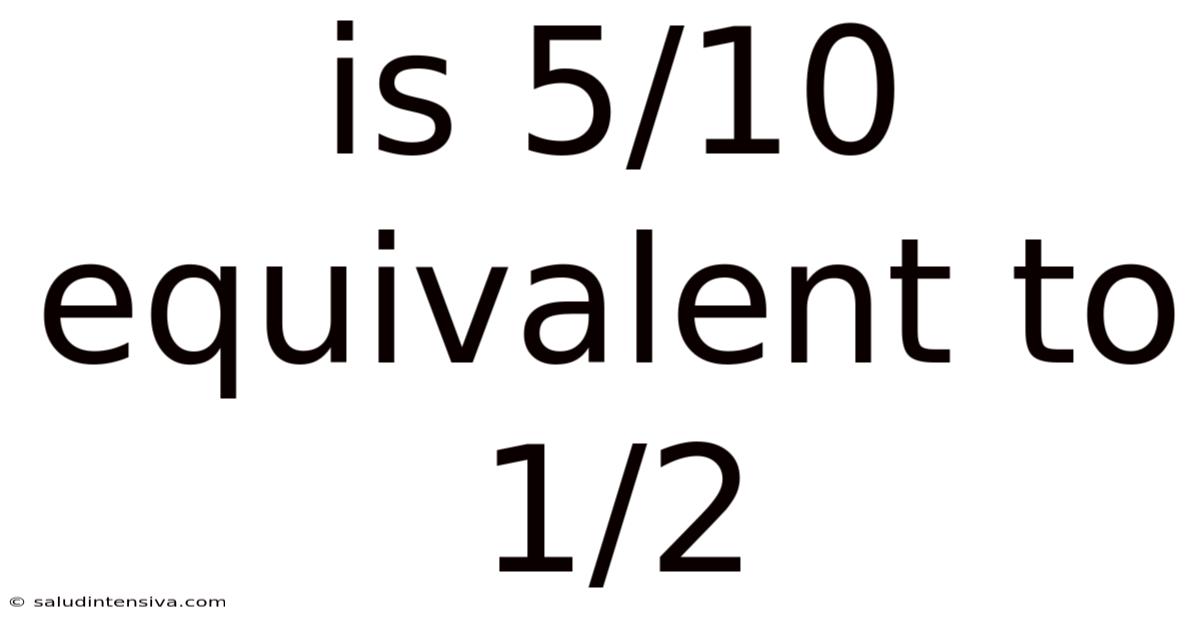
Table of Contents
Is 5/10 Equivalent to 1/2? A Deep Dive into Fractions and Equivalence
Are you struggling with fractions? Do you sometimes wonder if seemingly different fractions represent the same value? This comprehensive guide will explore the question, "Is 5/10 equivalent to 1/2?", delving into the fundamental concepts of fractions, equivalence, simplification, and providing practical examples to solidify your understanding. Understanding fraction equivalence is crucial for mastering arithmetic, algebra, and numerous real-world applications.
Understanding Fractions: Parts of a Whole
A fraction represents a part of a whole. It consists of two main components:
- Numerator: The top number indicates the number of parts you have.
- Denominator: The bottom number indicates the total number of equal parts the whole is divided into.
For example, in the fraction 3/4, the numerator (3) tells us we have three parts, and the denominator (4) tells us the whole is divided into four equal parts.
The Concept of Fraction Equivalence
Two fractions are considered equivalent if they represent the same proportion or value, even though they may look different. This means they represent the same amount of the whole. Think of it like cutting a pizza: you can have half a pizza, whether it's one out of two slices or five out of ten slices. Both represent the same amount of pizza.
Simplifying Fractions: Finding the Simplest Form
Simplifying a fraction means reducing it to its simplest form, where the numerator and denominator have no common factors other than 1. This is done by dividing both the numerator and the denominator by their greatest common divisor (GCD).
For example, let's simplify the fraction 6/12. The GCD of 6 and 12 is 6. Dividing both the numerator and the denominator by 6, we get:
6 ÷ 6 / 12 ÷ 6 = 1/2
This shows that 6/12 and 1/2 are equivalent fractions.
Is 5/10 Equivalent to 1/2? A Step-by-Step Analysis
Now, let's address the central question: Is 5/10 equivalent to 1/2?
To determine if two fractions are equivalent, we can use several methods:
Method 1: Simplification
Let's simplify the fraction 5/10. The GCD of 5 and 10 is 5. Dividing both the numerator and the denominator by 5, we get:
5 ÷ 5 / 10 ÷ 5 = 1/2
This clearly shows that 5/10 simplifies to 1/2. Therefore, yes, 5/10 is equivalent to 1/2.
Method 2: Cross-Multiplication
Another way to check for equivalence is through cross-multiplication. We multiply the numerator of one fraction by the denominator of the other, and vice versa. If the products are equal, the fractions are equivalent.
Let's apply this to 5/10 and 1/2:
5 x 2 = 10 10 x 1 = 10
Since both products are equal (10 = 10), we confirm that 5/10 is equivalent to 1/2.
Method 3: Visual Representation
Visual aids can be incredibly helpful in understanding fraction equivalence. Imagine a rectangular pizza cut into ten equal slices. If you take five slices, you have 5/10 of the pizza. Now imagine the same pizza cut into only two equal halves. Taking one half is the same as taking five out of ten slices. Both scenarios represent the same amount of pizza – half.
Real-World Applications of Fraction Equivalence
Understanding fraction equivalence is not just an academic exercise; it has numerous practical applications in everyday life:
- Cooking and Baking: Recipes often require adjusting ingredient amounts. Knowing how to simplify and find equivalent fractions is vital for accurate scaling.
- Measurement: Converting units of measurement frequently involves working with equivalent fractions (e.g., converting inches to feet).
- Finance: Calculating percentages, discounts, and interest often necessitates working with fractions.
- Construction and Engineering: Precise measurements and calculations in these fields rely heavily on fraction equivalence.
Common Mistakes and Misconceptions
While the concept of fraction equivalence is relatively straightforward, some common mistakes can occur:
- Incorrect Simplification: Failing to find the greatest common divisor can lead to an incomplete simplification.
- Misunderstanding Cross-Multiplication: Incorrectly applying the cross-multiplication method can lead to erroneous conclusions about equivalence.
- Ignoring the Whole: Remember that fractions always represent a part of a whole. When comparing fractions, ensure you are comparing parts of the same whole.
Frequently Asked Questions (FAQ)
Q: Can any fraction be simplified?
A: Not all fractions can be simplified. A fraction is already in its simplest form if the numerator and denominator have no common factors other than 1 (e.g., 3/7).
Q: What happens if I divide the numerator and denominator by a number that is not their GCD?
A: You will get an equivalent fraction, but it won't be in its simplest form.
Q: Is there a limit to the number of equivalent fractions a given fraction can have?
A: No, there are infinitely many equivalent fractions for any given fraction.
Q: How can I practice understanding fraction equivalence?
A: Practice makes perfect! Work through various examples, use visual aids like diagrams and fraction bars, and utilize online resources and worksheets.
Conclusion: Mastering Fractions for a Brighter Future
This in-depth exploration of fraction equivalence, focusing on the example of 5/10 and 1/2, aims to solidify your understanding of this fundamental mathematical concept. Mastering fractions is not just about passing tests; it's about developing a crucial skill set that will serve you well in various aspects of life, from everyday tasks to complex problem-solving in professional settings. By understanding the underlying principles of simplification, cross-multiplication, and visual representation, you can confidently tackle fraction problems and appreciate the elegance and practicality of this mathematical tool. Remember that consistent practice and a thorough understanding of the underlying concepts are key to mastering fractions and unlocking their immense potential. So, keep practicing, and soon, you'll be confidently navigating the world of fractions with ease!
Latest Posts
Latest Posts
-
What Is Half Of 1 5
Sep 12, 2025
-
Square Cm To Square Feet
Sep 12, 2025
-
4 9 To A Decimal
Sep 12, 2025
-
Percentage Change With Negative Numbers
Sep 12, 2025
-
Roman Numeral Tattoo Font Generator
Sep 12, 2025
Related Post
Thank you for visiting our website which covers about Is 5/10 Equivalent To 1/2 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.