Is 6/10 Equivalent To 3/5
saludintensiva
Sep 11, 2025 · 5 min read
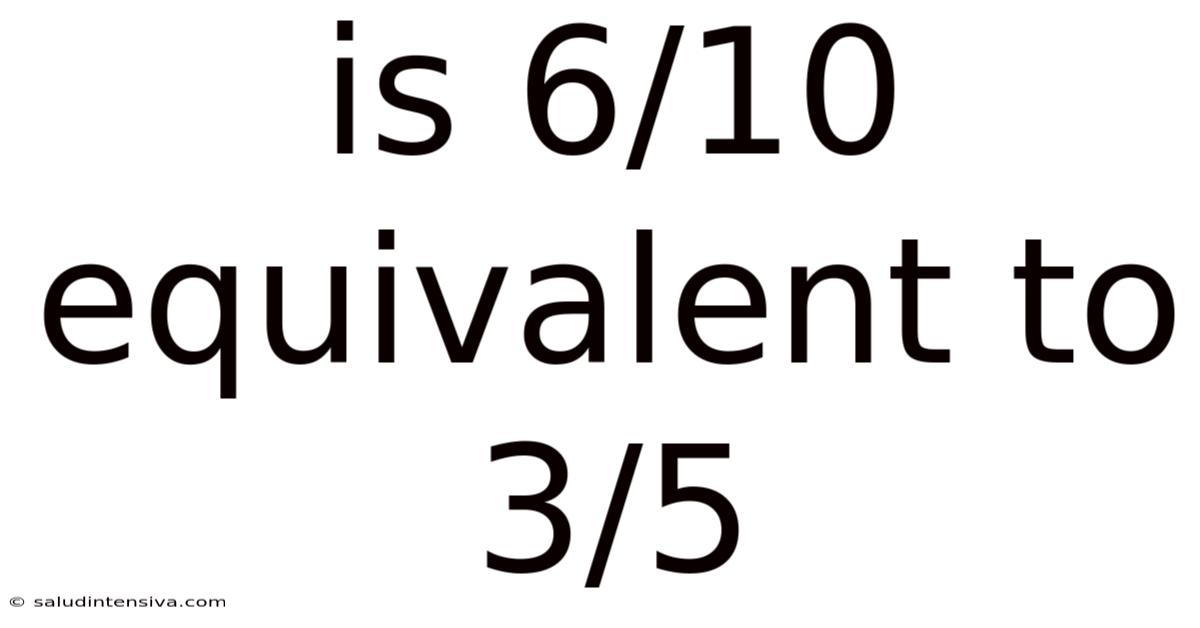
Table of Contents
Is 6/10 Equivalent to 3/5? A Deep Dive into Fraction Equivalence
Are you struggling with fractions? Understanding fraction equivalence is a fundamental skill in mathematics, crucial for everything from baking a cake to calculating complex engineering problems. This article will thoroughly explore the question: Is 6/10 equivalent to 3/5? We'll delve into the concept of equivalent fractions, explore different methods for determining equivalence, and provide practical examples to solidify your understanding. By the end, you'll be confident in identifying equivalent fractions and applying this knowledge to various mathematical situations.
Understanding Equivalent Fractions
Equivalent fractions represent the same portion of a whole, even though they may look different. Imagine you have a pizza cut into 10 slices. Eating 6 slices represents 6/10 of the pizza. Now imagine the same pizza cut into 5 slices. Eating 3 slices represents 3/5 of the pizza. Both scenarios represent the same amount of pizza consumed. This is the core concept of equivalent fractions: different fractions can represent the same value.
Methods for Determining Fraction Equivalence
There are several ways to determine if two fractions are equivalent. Let's explore the most common methods:
1. Simplifying Fractions
The most straightforward method is to simplify, or reduce, each fraction to its simplest form. A fraction is in its simplest form when the greatest common divisor (GCD) of the numerator and denominator is 1. The GCD is the largest number that divides both the numerator and the denominator without leaving a remainder.
Let's simplify 6/10:
- Find the GCD of 6 and 10: The factors of 6 are 1, 2, 3, and 6. The factors of 10 are 1, 2, 5, and 10. The greatest common factor is 2.
- Divide both the numerator and denominator by the GCD: 6 ÷ 2 = 3 and 10 ÷ 2 = 5.
Therefore, the simplest form of 6/10 is 3/5.
Now let's look at 3/5. The GCD of 3 and 5 is 1, meaning 3/5 is already in its simplest form.
Since both 6/10 and 3/5 simplify to 3/5, they are equivalent fractions.
2. Cross-Multiplication
Cross-multiplication provides another effective method for determining fraction equivalence. To use this method, multiply the numerator of one fraction by the denominator of the other fraction, and vice versa. If the products are equal, the fractions are equivalent.
Let's apply cross-multiplication to 6/10 and 3/5:
- Multiply the numerator of 6/10 (6) by the denominator of 3/5 (5): 6 x 5 = 30
- Multiply the denominator of 6/10 (10) by the numerator of 3/5 (3): 10 x 3 = 30
Since both products are equal (30 = 30), the fractions 6/10 and 3/5 are equivalent.
3. Using Visual Representations
Visual aids, such as fraction bars or pie charts, can be incredibly helpful, especially when teaching younger students or those who are visual learners. Representing 6/10 and 3/5 visually will clearly demonstrate their equivalence.
Imagine two identical circles. Divide the first circle into 10 equal slices and shade 6 of them. Divide the second circle into 5 equal slices and shade 3 of them. You'll see that the shaded area in both circles is identical, visually confirming that 6/10 and 3/5 represent the same portion of the whole.
The Importance of Understanding Equivalent Fractions
The ability to identify and work with equivalent fractions is paramount in many areas of mathematics and beyond. Here are some key applications:
- Simplifying Calculations: Working with simplified fractions makes calculations easier and less prone to errors. For example, adding 6/10 + 2/10 is more challenging than adding 3/5 + 2/10 (after simplifying 6/10).
- Comparing Fractions: Determining which fraction is larger or smaller is simplified when fractions are expressed in their simplest form or as equivalent fractions with a common denominator.
- Solving Equations: Many algebraic equations involve fractions, and manipulating fractions using the concept of equivalence is crucial for finding solutions.
- Real-World Applications: Fractions are ubiquitous in daily life—from cooking and baking to calculating discounts and proportions. Understanding equivalence ensures accurate measurements and calculations.
Further Exploration: Beyond 6/10 and 3/5
While we've focused on 6/10 and 3/5, the principles of fraction equivalence extend to all fractions. Let's consider some examples:
- 1/2 and 2/4: Both simplify to 1/2.
- 3/6 and 1/2: Both simplify to 1/2.
- 4/8 and 1/2: Both simplify to 1/2.
Notice a pattern? All these fractions are equivalent to 1/2. This highlights that many fractions can represent the same value.
Frequently Asked Questions (FAQ)
Q: Why is simplifying fractions important?
A: Simplifying fractions makes them easier to work with, reduces the risk of errors in calculations, and makes comparing fractions simpler.
Q: Can any fraction be simplified?
A: Not all fractions can be simplified. A fraction is already in its simplest form if its numerator and denominator have a greatest common divisor (GCD) of 1.
Q: What if I get different products when cross-multiplying?
A: If the products are different when cross-multiplying, the fractions are not equivalent.
Q: Are there other methods to determine fraction equivalence?
A: Yes, you can also convert fractions to decimals and compare the decimal values. If the decimal values are the same, the fractions are equivalent.
Q: How can I improve my understanding of fractions?
A: Practice is key! Work through various exercises, use visual aids, and seek help when needed. Online resources and educational materials can provide additional support.
Conclusion
In conclusion, yes, 6/10 is equivalent to 3/5. Understanding fraction equivalence is a fundamental mathematical concept with broad applications. By mastering the methods of simplifying fractions and cross-multiplication, you can confidently determine fraction equivalence and apply this knowledge to a wide range of mathematical problems and real-world situations. Remember to practice regularly and utilize various methods to solidify your understanding. With consistent effort, you’ll become proficient in working with fractions and unlock a deeper understanding of mathematics.
Latest Posts
Latest Posts
-
Price Per Kg To Lb
Sep 11, 2025
-
Gcf Of Two Monomials Calculator
Sep 11, 2025
-
5 To The Power 4
Sep 11, 2025
-
What Is Half Of 13
Sep 11, 2025
-
Terminating Or Repeating Decimal Calculator
Sep 11, 2025
Related Post
Thank you for visiting our website which covers about Is 6/10 Equivalent To 3/5 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.