Is 6/10 Greater Than 1/2
saludintensiva
Sep 12, 2025 · 5 min read
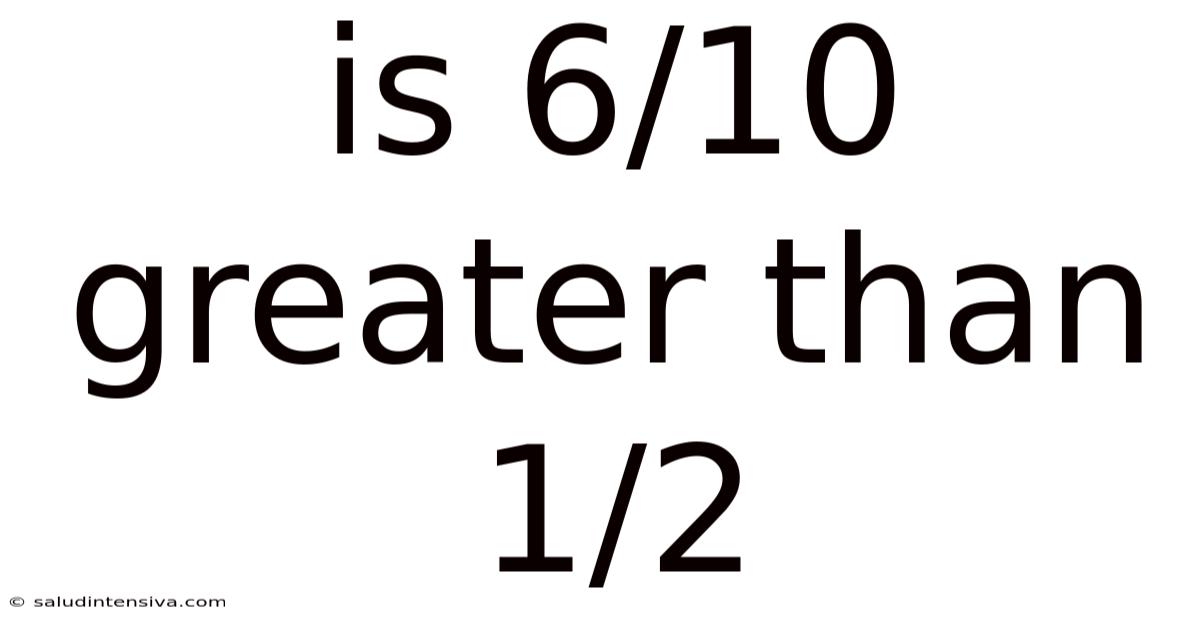
Table of Contents
Is 6/10 Greater Than 1/2? A Deep Dive into Fraction Comparison
Are you struggling with comparing fractions? Many find comparing fractions like 6/10 and 1/2 challenging. This comprehensive guide will not only answer the question, "Is 6/10 greater than 1/2?" but also equip you with the skills and understanding to compare any two fractions confidently. We'll explore various methods, from visual representations to mathematical calculations, ensuring you grasp the concepts thoroughly.
Understanding Fractions: A Quick Refresher
Before we dive into comparing 6/10 and 1/2, let's quickly review what a fraction represents. A fraction is a part of a whole. It's written as a numerator (the top number) over a denominator (the bottom number), separated by a line. The numerator tells us how many parts we have, and the denominator tells us how many equal parts the whole is divided into. For instance, in the fraction 1/2, the numerator (1) indicates we have one part, and the denominator (2) indicates the whole is divided into two equal parts.
Method 1: Visual Comparison
One of the easiest ways to compare fractions is through visual representation. Let's use diagrams to compare 6/10 and 1/2.
Imagine a rectangle divided into 10 equal parts. Shading 6 of those parts represents 6/10.
[Insert a rectangle divided into 10 equal parts, with 6 parts shaded.]
Now, imagine another rectangle of the same size divided into 2 equal parts. Shading one part represents 1/2.
[Insert a rectangle divided into 2 equal parts, with 1 part shaded.]
By visually comparing the shaded areas, it's apparent that 6/10 represents a smaller portion of the whole than 1/2. This visual comparison provides an intuitive understanding of the fraction's relative sizes.
Method 2: Finding a Common Denominator
A more robust mathematical approach involves finding a common denominator. This means finding a number that is a multiple of both denominators (10 and 2). The lowest common multiple (LCM) of 10 and 2 is 10.
To convert 1/2 to a fraction with a denominator of 10, we multiply both the numerator and denominator by 5:
(1 * 5) / (2 * 5) = 5/10
Now we can easily compare 6/10 and 5/10. Since 6 > 5, we conclude that 6/10 > 5/10. Therefore, 6/10 is greater than 1/2.
Method 3: Converting to Decimals
Another effective method is to convert both fractions to decimals. To convert a fraction to a decimal, we simply divide the numerator by the denominator.
6/10 = 0.6
1/2 = 0.5
Comparing the decimal values, 0.6 > 0.5. Therefore, 6/10 is greater than 1/2. This method is particularly useful when dealing with fractions that are difficult to compare using common denominators.
Method 4: Comparing to a Benchmark Fraction
Using benchmark fractions (like 1/2, 1/4, 3/4, etc.) can simplify comparisons. We know that 1/2 represents 0.5. Since 6/10 is equivalent to 0.6, which is greater than 0.5, 6/10 is greater than 1/2. This method is quick and efficient for simple comparisons.
The Importance of Understanding Fraction Comparison
Mastering fraction comparison is crucial for success in mathematics and many other fields. It's a foundational skill that underlies more advanced concepts in algebra, calculus, and even everyday tasks like cooking and measurement. Understanding how to compare fractions allows you to solve problems involving ratios, proportions, and percentages effectively.
Beyond 6/10 and 1/2: A Broader Perspective
While we’ve focused on comparing 6/10 and 1/2, the principles discussed apply to comparing any two fractions. The methods outlined – visual comparison, finding a common denominator, converting to decimals, and using benchmark fractions – provide a versatile toolkit for tackling fraction comparisons of any complexity. Remember to choose the method that best suits the specific fractions you're working with.
Frequently Asked Questions (FAQ)
-
Q: What if the denominators have no common factor? A: If the denominators are relatively prime (have no common factors other than 1), you'll need to find the least common multiple (LCM) of the denominators. This will involve multiplying the denominators together, then converting each fraction to an equivalent fraction with the LCM as the denominator.
-
Q: Can I always use decimals to compare fractions? A: Yes, converting to decimals is always a valid method. However, sometimes working with fractions directly is simpler and more accurate, especially if the decimal representation is a repeating decimal (like 1/3 = 0.333...).
-
Q: Are there any other ways to compare fractions? A: Yes. You can also use cross-multiplication. To compare fractions a/b and c/d, you cross-multiply: ad and bc. If ad > bc, then a/b > c/d.
-
Q: Why is understanding fraction comparison important in real life? A: Fraction comparison is vital for tasks involving recipes, measuring ingredients, understanding proportions in construction or design, and interpreting data presented in graphs and charts.
-
Q: How can I practice comparing fractions? A: Practice regularly with different types of fractions. You can find numerous worksheets and online resources that provide practice problems with varying levels of difficulty.
Conclusion: Mastering the Art of Fraction Comparison
Determining whether 6/10 is greater than 1/2 is not just about arriving at a correct answer ("Yes, 6/10 is greater than 1/2"); it's about understanding the underlying principles of fraction comparison. By mastering the various techniques discussed – visual comparison, finding a common denominator, converting to decimals, and using benchmark fractions – you build a strong foundation for success in mathematics and beyond. Remember, practice is key. The more you work with fractions, the more confident and proficient you'll become in comparing them accurately and efficiently. Embrace the challenge, and you'll soon find yourself navigating the world of fractions with ease and confidence.
Latest Posts
Latest Posts
-
9 1 100 As A Decimal
Sep 12, 2025
-
1 8 Times 1 8
Sep 12, 2025
-
3 1 4 3 4
Sep 12, 2025
-
80 100 As A Decimal
Sep 12, 2025
-
Lcm Of 8 9 10
Sep 12, 2025
Related Post
Thank you for visiting our website which covers about Is 6/10 Greater Than 1/2 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.