Is 6/8 Equal To 9/12
saludintensiva
Sep 20, 2025 · 6 min read
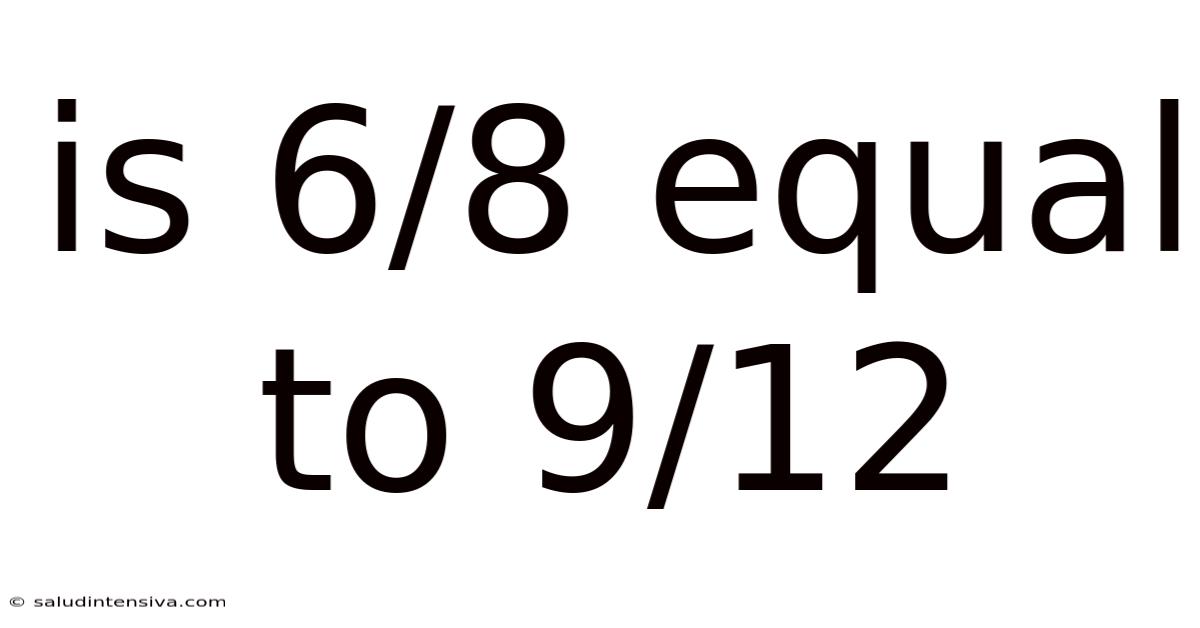
Table of Contents
Is 6/8 Equal to 9/12? A Deep Dive into Fraction Equivalence
Are you grappling with fractions? Understanding whether 6/8 is equal to 9/12 is a fundamental concept in mathematics, crucial for everything from baking a cake to understanding complex engineering problems. This article will not only answer this question definitively but will also equip you with the knowledge and tools to confidently determine the equivalence of any two fractions. We'll explore various methods, delve into the underlying mathematical principles, and address common misconceptions. Let's dive in!
Understanding Fractions: The Building Blocks
Before we tackle the core question, let's refresh our understanding of fractions. A fraction represents a part of a whole. It's expressed as a ratio of two numbers: the numerator (the top number) and the denominator (the bottom number). The denominator indicates how many equal parts the whole is divided into, while the numerator shows how many of those parts are being considered.
For example, in the fraction 3/4, the denominator (4) tells us the whole is divided into four equal parts, and the numerator (3) indicates we're considering three of those parts.
Method 1: Simplifying Fractions to Their Lowest Terms
The simplest and most intuitive way to determine if 6/8 is equal to 9/12 is by simplifying both fractions to their lowest terms. This means finding the greatest common divisor (GCD) of the numerator and denominator and dividing both by that number.
-
Simplifying 6/8: The GCD of 6 and 8 is 2. Dividing both the numerator and denominator by 2, we get 6/2 = 3 and 8/2 = 4. Therefore, 6/8 simplifies to 3/4.
-
Simplifying 9/12: The GCD of 9 and 12 is 3. Dividing both the numerator and denominator by 3, we get 9/3 = 3 and 12/3 = 4. Therefore, 9/12 simplifies to 3/4.
Since both 6/8 and 9/12 simplify to the same fraction, 3/4, we can confidently conclude that yes, 6/8 is equal to 9/12.
Method 2: Cross-Multiplication
Another effective method for comparing fractions is cross-multiplication. This involves multiplying the numerator of one fraction by the denominator of the other, and vice versa. If the products are equal, the fractions are equivalent.
Let's apply this to 6/8 and 9/12:
- Multiply the numerator of 6/8 (6) by the denominator of 9/12 (12): 6 * 12 = 72
- Multiply the denominator of 6/8 (8) by the numerator of 9/12 (9): 8 * 9 = 72
Since both products are equal (72 = 72), we again confirm that 6/8 is equal to 9/12.
Method 3: Finding a Common Denominator
This method involves converting both fractions to equivalent fractions with the same denominator. The least common multiple (LCM) of the denominators is often used as the common denominator.
-
Finding the LCM of 8 and 12: The multiples of 8 are 8, 16, 24, 32... The multiples of 12 are 12, 24, 36... The LCM of 8 and 12 is 24.
-
Converting 6/8: To get a denominator of 24, we multiply both the numerator and denominator by 3 (24/8 = 3): (6 * 3) / (8 * 3) = 18/24
-
Converting 9/12: To get a denominator of 24, we multiply both the numerator and denominator by 2 (24/12 = 2): (9 * 2) / (12 * 2) = 18/24
Both fractions are now expressed as 18/24, confirming that 6/8 is equal to 9/12.
The Mathematical Principle Behind Fraction Equivalence
The equivalence of fractions is based on the fundamental principle of multiplying or dividing both the numerator and denominator by the same non-zero number. This operation doesn't change the value of the fraction; it simply represents the same proportion in a different form. This is because fractions represent ratios, and multiplying or dividing both parts of a ratio by the same number maintains the same relationship between them.
Visual Representation: Understanding Equivalence
Imagine a pizza. If you cut it into 8 equal slices and take 6, you have 6/8 of the pizza. Now imagine another pizza, cut into 12 equal slices. If you take 9 slices, you have 9/12 of the pizza. While the number of slices is different, the amount of pizza you have in both cases is the same – exactly three-quarters of the pizza. This visual representation reinforces the concept of fraction equivalence.
Addressing Common Misconceptions
-
Adding Numerators and Denominators: A common mistake is adding the numerators and denominators separately to determine equivalence. This is incorrect. For example, 1/2 is not equal to 2/4 simply because 1+1≠2+2.
-
Ignoring Simplification: Failing to simplify fractions can lead to inaccurate comparisons. While 6/8 and 9/12 might seem different at first glance, simplifying them reveals their equivalence.
-
Misunderstanding Ratios: Equivalence involves maintaining the ratio between the numerator and denominator. Adding or subtracting a fixed number to both parts doesn't maintain the ratio.
Beyond the Basics: Applications of Fraction Equivalence
The ability to determine fraction equivalence is essential in numerous applications:
-
Cooking and Baking: Scaling recipes accurately requires understanding how to adjust ingredient quantities while maintaining the correct proportions.
-
Engineering and Construction: Precise measurements and calculations in various fields rely on correctly manipulating fractions.
-
Data Analysis: Understanding proportions and ratios in datasets requires the ability to compare and simplify fractions.
-
Financial Calculations: Working with percentages and proportions in finance often involves simplifying and comparing fractions.
Frequently Asked Questions (FAQs)
-
Q: Can I always find a common denominator? A: Yes, you can always find a common denominator, although the LCM (least common multiple) is the most efficient choice.
-
Q: Is there a fastest method to determine equivalence? A: Simplifying to the lowest terms is often the fastest and most efficient method, especially for larger numbers. Cross-multiplication is also quick and reliable.
-
Q: What if the fractions are negative? A: The principles remain the same. Compare the absolute values of the fractions using any of the methods described. If the absolute values are equal, and the signs are the same, the fractions are equivalent.
-
Q: Are all equivalent fractions represented by the same decimal value? A: Yes. Equivalent fractions, when converted to decimals, will always have the same decimal representation.
Conclusion
Determining whether 6/8 is equal to 9/12 is more than just solving a simple math problem; it's about grasping the core principles of fraction equivalence. By understanding the methods of simplification, cross-multiplication, and finding common denominators, you gain a powerful tool for manipulating and comparing fractions with confidence. This knowledge extends far beyond the classroom, proving invaluable in numerous real-world applications. Embrace these techniques, and you'll find working with fractions becomes easier and more intuitive. Remember to practice regularly – the more you work with fractions, the more comfortable and proficient you'll become!
Latest Posts
Latest Posts
-
Multiplication Fraction Word Problems Worksheet
Sep 20, 2025
-
11 5 Into A Decimal
Sep 20, 2025
-
Financial Calculator Vs Scientific Calculator
Sep 20, 2025
-
How Tall Is 63 Centimeters
Sep 20, 2025
-
What Is 3 8 In Metric
Sep 20, 2025
Related Post
Thank you for visiting our website which covers about Is 6/8 Equal To 9/12 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.