Is 7/16 Bigger Than 3/8
saludintensiva
Sep 17, 2025 · 6 min read
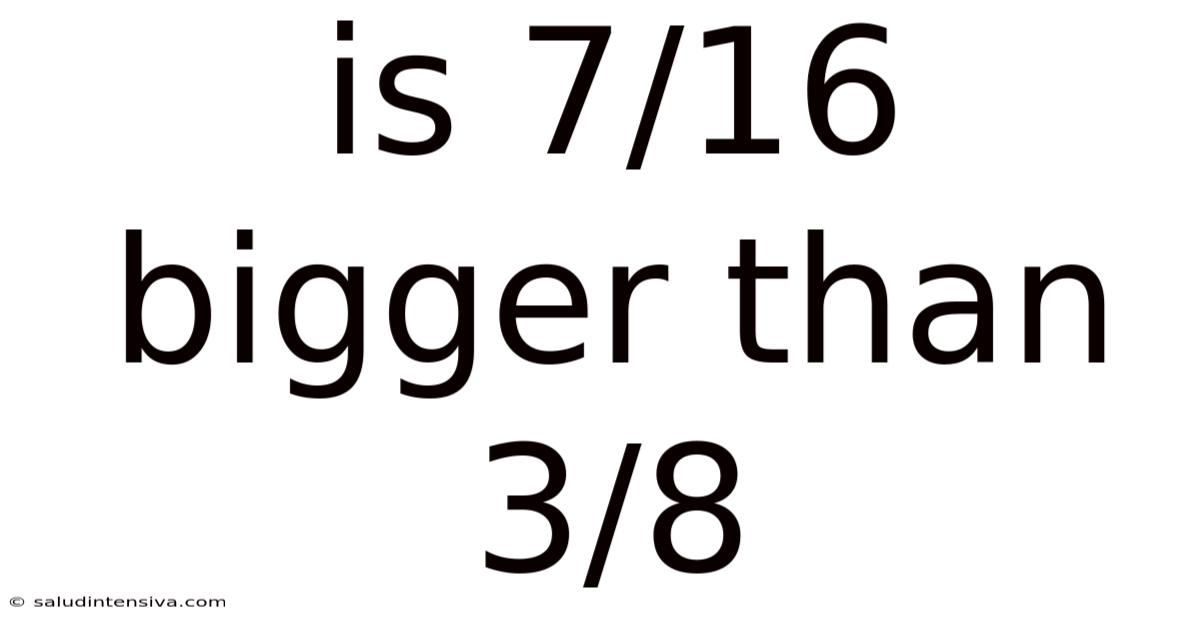
Table of Contents
Is 7/16 Bigger Than 3/8? A Deep Dive into Fraction Comparison
Understanding fractions is a fundamental skill in mathematics, essential for various applications in everyday life and advanced studies. This article will thoroughly explore the question, "Is 7/16 bigger than 3/8?", providing a step-by-step guide to comparing fractions and delving into the underlying mathematical principles. We'll go beyond a simple yes or no answer, offering a comprehensive understanding that empowers you to confidently compare any two fractions.
Introduction: Understanding Fractions
Before diving into the comparison, let's refresh our understanding of fractions. A fraction represents a part of a whole. It's expressed as a ratio of two numbers: the numerator (top number) and the denominator (bottom number). The denominator indicates the total number of equal parts the whole is divided into, while the numerator shows how many of those parts are being considered. For example, in the fraction 3/8, the denominator 8 tells us the whole is divided into 8 equal parts, and the numerator 3 indicates we're considering 3 of those parts.
Comparing Fractions: Different Approaches
There are several methods to compare fractions. Let's explore the most common and effective techniques:
1. Finding a Common Denominator
This is perhaps the most straightforward approach. To compare 7/16 and 3/8, we need to find a common denominator, which is a number that both 16 and 8 divide into evenly. In this case, the least common multiple (LCM) of 16 and 8 is 16.
-
Converting 3/8: To convert 3/8 to a fraction with a denominator of 16, we multiply both the numerator and the denominator by 2: (3 x 2) / (8 x 2) = 6/16.
-
Comparison: Now we can easily compare 7/16 and 6/16. Since 7 > 6, we can conclude that 7/16 is bigger than 6/16, and therefore 7/16 is bigger than 3/8.
2. Converting to Decimals
Another effective method is converting the fractions to decimals. This allows for a direct numerical comparison.
-
Converting 7/16 to a decimal: 7 ÷ 16 = 0.4375
-
Converting 3/8 to a decimal: 3 ÷ 8 = 0.375
-
Comparison: Comparing the decimal values, 0.4375 > 0.375. This confirms that 7/16 is bigger than 3/8.
3. Visual Representation
While less precise for complex fractions, visual representation can be helpful for understanding the concept. Imagine two identical pies.
-
7/16: Divide one pie into 16 equal slices and shade 7 of them.
-
3/8: Divide the other pie into 8 equal slices and shade 3 of them.
By visually comparing the shaded portions, it becomes apparent that the 7/16 pie has a larger shaded area than the 3/8 pie. This provides a clear visual confirmation that 7/16 is bigger than 3/8.
A Deeper Dive: Understanding Least Common Multiple (LCM)
The LCM is crucial when comparing fractions using the common denominator method. The LCM of two or more numbers is the smallest number that is a multiple of all the numbers. Finding the LCM can be done in several ways:
-
Listing Multiples: List the multiples of each number until you find the smallest common multiple. For 16 and 8:
- Multiples of 16: 16, 32, 48, ...
- Multiples of 8: 8, 16, 24, 32, ... The smallest common multiple is 16.
-
Prime Factorization: Break down each number into its prime factors. The LCM is the product of the highest powers of all prime factors present in the numbers.
- 16 = 2 x 2 x 2 x 2 = 2⁴
- 8 = 2 x 2 x 2 = 2³ The LCM is 2⁴ = 16.
Understanding the LCM allows for efficient comparison of fractions with different denominators, a fundamental skill in algebra and beyond.
Beyond the Basics: Extending Fraction Comparison Skills
The techniques discussed above can be applied to compare any two fractions, regardless of their complexity. Here are some additional considerations:
-
Improper Fractions: An improper fraction has a numerator larger than or equal to its denominator (e.g., 7/4). When comparing improper fractions, the same methods apply. Converting to decimals or finding a common denominator will reveal which fraction is larger.
-
Mixed Numbers: A mixed number combines a whole number and a fraction (e.g., 1 3/4). To compare mixed numbers, you can either convert them to improper fractions and then apply the usual comparison methods, or compare the whole numbers first and then the fractional parts if the whole numbers are equal.
-
Negative Fractions: When comparing negative fractions, remember that the smaller the absolute value (ignoring the negative sign), the larger the number. For example, -1/2 is larger than -3/4 because -1/2 is closer to 0 on the number line.
Frequently Asked Questions (FAQ)
Q1: Why is finding a common denominator important when comparing fractions?
A1: Finding a common denominator allows us to express the fractions with the same denominator, making direct comparison of the numerators possible. Without a common denominator, it's difficult to determine which fraction represents a larger portion of the whole.
Q2: Can I always use decimal conversion to compare fractions?
A2: While decimal conversion is a valid method, it's not always the most efficient. Some fractions, when converted to decimals, result in repeating or non-terminating decimals, making the comparison less straightforward. Finding a common denominator often provides a cleaner and more precise comparison.
Q3: Are there any shortcuts for comparing fractions?
A3: While no universal shortcut exists, recognizing simple relationships can sometimes expedite the process. For example, if one fraction's numerator and denominator are both larger than the other fraction's, it may be larger, but this is not always the case. The reliable methods remain finding a common denominator or converting to decimals.
Q4: How can I improve my understanding of fractions?
A4: Practice is key! Work through numerous examples, utilizing different comparison methods. Visual aids, like pie charts or fraction bars, can help solidify your understanding. Consider exploring online resources and educational materials dedicated to fractions.
Conclusion: Mastering Fraction Comparison
Comparing fractions is a crucial skill in mathematics. By understanding the principles of finding a common denominator, converting to decimals, and employing visual representations, you can confidently determine which fraction is larger. Remember that mastering this skill involves not just memorizing methods but understanding the underlying concepts of fractions and their representation of parts of a whole. The ability to accurately compare fractions forms a solid foundation for more advanced mathematical concepts and applications in various fields. Continue practicing and exploring different approaches; your understanding and proficiency will steadily grow.
Latest Posts
Latest Posts
-
1 25 In Decimal Form
Sep 18, 2025
-
Scientific Notation And Significant Figures
Sep 18, 2025
-
Improper Fraction For 1 1 2
Sep 18, 2025
-
What Percent Is 11 12
Sep 18, 2025
-
Cuantas Libras Son 70 Kg
Sep 18, 2025
Related Post
Thank you for visiting our website which covers about Is 7/16 Bigger Than 3/8 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.