Is 7/8 Greater Than 1/2
saludintensiva
Sep 15, 2025 · 5 min read
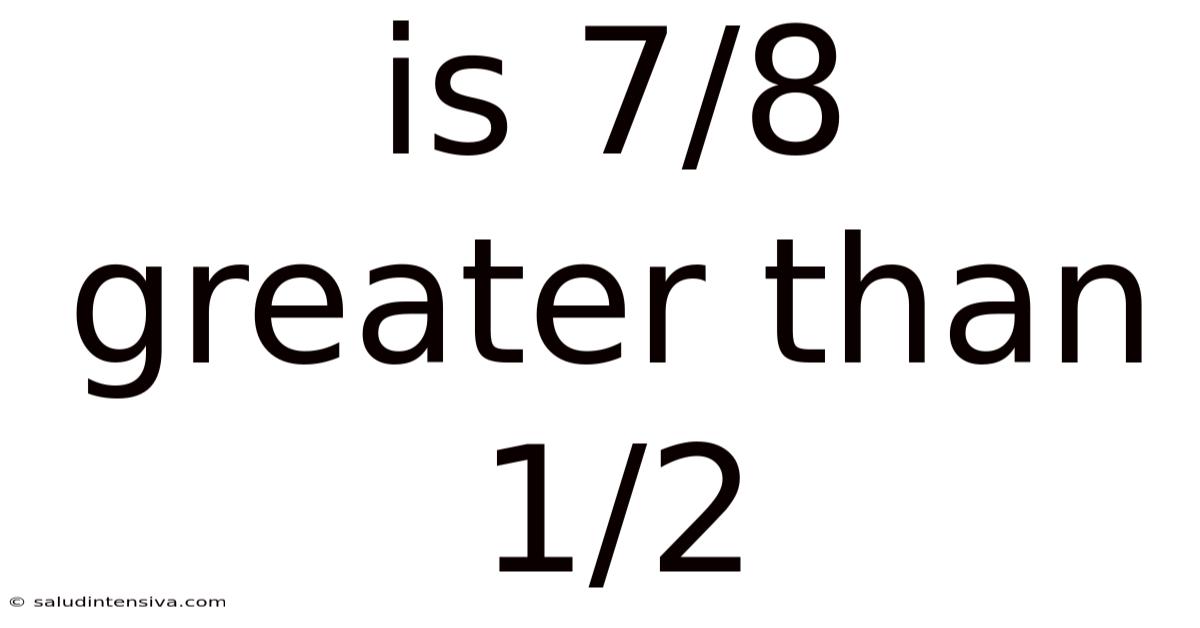
Table of Contents
Is 7/8 Greater Than 1/2? A Deep Dive into Fraction Comparison
Understanding fractions is a fundamental skill in mathematics, crucial for everything from baking a cake to understanding complex financial reports. One common question that arises, particularly for students learning about fractions, is whether 7/8 is greater than 1/2. This article will not only definitively answer this question but also explore the underlying principles of comparing fractions, providing you with the tools to confidently tackle similar comparisons in the future. We'll delve into various methods, visual representations, and even touch upon the mathematical reasoning behind it all.
Introduction: Understanding Fractions
Before we tackle the specific comparison of 7/8 and 1/2, let's refresh our understanding of fractions. A fraction represents a part of a whole. It's composed of two key components:
- Numerator: The top number, indicating the number of parts we have.
- Denominator: The bottom number, indicating the total number of equal parts the whole is divided into.
For instance, in the fraction 7/8, 7 is the numerator (the number of parts we have), and 8 is the denominator (the total number of equal parts). This means we have 7 out of 8 equal parts of a whole.
Method 1: Visual Comparison using Fraction Bars
A simple and intuitive way to compare fractions is by using visual aids like fraction bars or pie charts. Imagine two identical bars representing the whole. One bar is divided into 8 equal parts, with 7 of them shaded (representing 7/8). The other bar is divided into 2 equal parts, with 1 part shaded (representing 1/2).
By visually inspecting these bars, it’s immediately apparent that the area representing 7/8 is significantly larger than the area representing 1/2. This visual comparison provides a clear, intuitive understanding of why 7/8 is greater than 1/2.
Method 2: Finding a Common Denominator
A more formal mathematical approach involves finding a common denominator for both fractions. This means finding a number that is a multiple of both denominators (8 and 2). The least common multiple (LCM) of 8 and 2 is 8.
- Converting 7/8: This fraction already has a denominator of 8, so it remains 7/8.
- Converting 1/2: To convert 1/2 to have a denominator of 8, we multiply both the numerator and the denominator by 4: (1 x 4) / (2 x 4) = 4/8.
Now that both fractions have the same denominator, we can easily compare their numerators. Since 7 > 4, we conclude that 7/8 > 4/8, therefore 7/8 > 1/2.
Method 3: Converting to Decimals
Another effective method is to convert both fractions into decimals. This involves dividing the numerator by the denominator.
- Converting 7/8 to a decimal: 7 ÷ 8 = 0.875
- Converting 1/2 to a decimal: 1 ÷ 2 = 0.5
Comparing the decimal values, 0.875 > 0.5, confirming that 7/8 is greater than 1/2. This method is particularly useful when dealing with more complex fractions or when using a calculator.
Method 4: Understanding the Relative Sizes of the Fractions
We can also approach this intuitively by considering the relative positions of the fractions on a number line. 1/2 represents the midpoint between 0 and 1. 7/8 is much closer to 1 than to 0. Since 7/8 is closer to 1 than 1/2 is, and 1 is greater than 1/2, we can deduce that 7/8 is greater than 1/2. This method promotes a deeper understanding of fractional values.
The Mathematical Reasoning Behind Fraction Comparison
The core principle underlying all these methods is the concept of relative size. When comparing fractions, we are essentially comparing the relative portions they represent of a whole. Finding a common denominator allows for a direct comparison of the numerators, as it ensures that we are comparing the same-sized parts. Converting to decimals provides a numerical representation that allows for easy comparison.
Exploring Further: Comparing Fractions with Different Numerators and Denominators
The techniques we've discussed are applicable to comparing any two fractions, regardless of their numerators and denominators. Let's consider another example: Is 5/6 greater than 2/3?
- Common Denominator: The LCM of 6 and 3 is 6. 5/6 remains as 5/6, and 2/3 becomes (2 x 2) / (3 x 2) = 4/6. Since 5 > 4, 5/6 > 2/3.
- Decimal Conversion: 5/6 ≈ 0.833 and 2/3 ≈ 0.667. Again, 0.833 > 0.667, confirming that 5/6 > 2/3.
These examples illustrate the versatility and reliability of these methods.
Frequently Asked Questions (FAQ)
Q1: Can I always use the common denominator method to compare fractions?
A1: Yes, the common denominator method is a universally applicable and reliable technique for comparing fractions. It's a foundational concept in fraction arithmetic.
Q2: Is it easier to compare fractions using decimals or common denominators?
A2: The choice between decimals and common denominators often depends on personal preference and the complexity of the fractions. For simple fractions, the common denominator method can be quicker. For more complex fractions or when using a calculator, converting to decimals might be more efficient.
Q3: Are there other visual methods for comparing fractions besides fraction bars?
A3: Yes, pie charts are another effective visual representation for comparing fractions. They provide a clear, intuitive way to visualize the relative sizes of the fractions.
Q4: What if the fractions have very large numbers?
A4: Even with large numbers, the principles remain the same. Finding the common denominator or converting to decimals might be more time-consuming but will still lead to the correct comparison. Using a calculator becomes highly beneficial in such scenarios.
Conclusion: Mastering Fraction Comparison
Comparing fractions is a fundamental mathematical skill. This article has explored multiple effective methods for determining whether one fraction is greater than another. Whether you use visual representations, find a common denominator, convert to decimals, or employ intuitive reasoning, the key is understanding the underlying concept of relative size and applying a consistent method. With practice, comparing fractions will become second nature, enhancing your mathematical proficiency and problem-solving abilities. Remember, the core concept is to understand what the fraction represents in terms of a part of a whole, and then find a way to compare those parts directly. By mastering these techniques, you'll be well-equipped to handle various fraction-related challenges with confidence. So, go ahead and practice! You've got this!
Latest Posts
Latest Posts
-
Height Of A Cone Calculator
Sep 15, 2025
-
Equivalent Fractions Of 4 7
Sep 15, 2025
-
5 To The First Power
Sep 15, 2025
-
Gcf Of 18 And 60
Sep 15, 2025
-
1 4 As Improper Fraction
Sep 15, 2025
Related Post
Thank you for visiting our website which covers about Is 7/8 Greater Than 1/2 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.