Lcm For 7 And 10
saludintensiva
Sep 16, 2025 · 6 min read
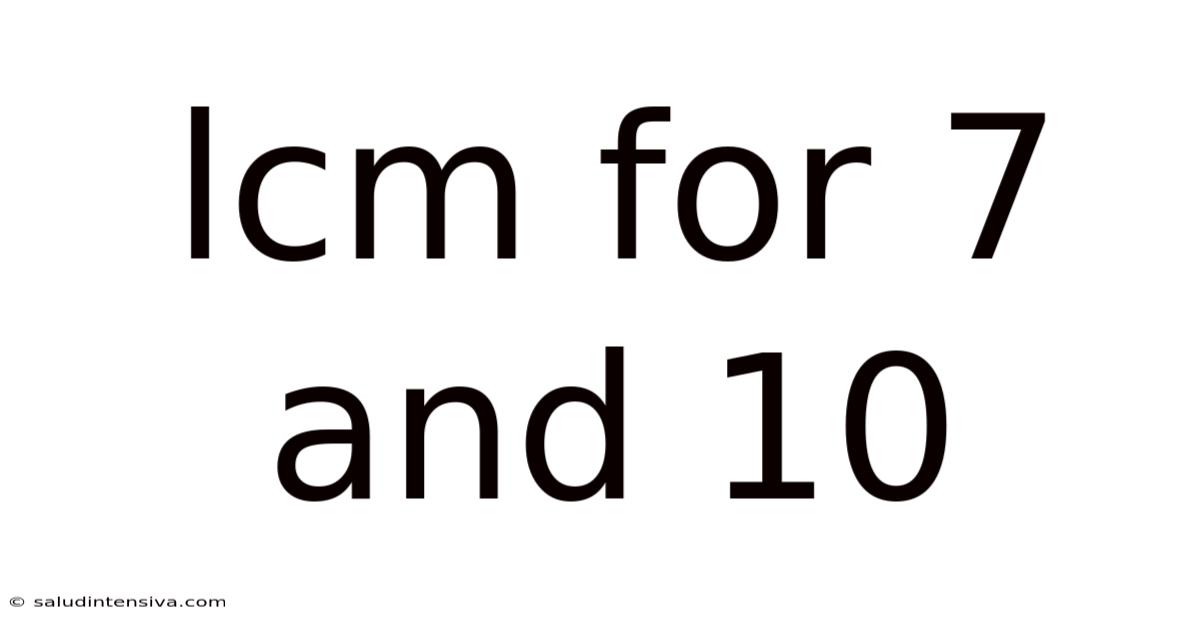
Table of Contents
Finding the Least Common Multiple (LCM) of 7 and 10: A Comprehensive Guide
Finding the least common multiple (LCM) might seem like a simple arithmetic task, but understanding the underlying concepts unlocks a deeper appreciation for number theory and its applications in various fields. This comprehensive guide explores the LCM of 7 and 10, explaining multiple methods to calculate it and demonstrating its relevance beyond basic mathematics. We'll delve into the theoretical foundations, providing you with a robust understanding of LCM and its practical uses.
Introduction: What is the LCM?
The least common multiple (LCM) of two or more integers is the smallest positive integer that is divisible by all the integers. It's a fundamental concept in number theory with applications in areas like scheduling, calculating fractions, and simplifying complex mathematical problems. For instance, understanding LCM is crucial when determining the least amount of time it takes for two events to occur simultaneously, or when finding the common denominator when adding or subtracting fractions. In this article, we'll focus on finding the LCM of 7 and 10, illustrating various methods and their underlying principles.
Method 1: Listing Multiples
This is the most straightforward approach, particularly useful for smaller numbers. We list the multiples of each number until we find the smallest multiple common to both.
- Multiples of 7: 7, 14, 21, 28, 35, 42, 49, 56, 63, 70, ...
- Multiples of 10: 10, 20, 30, 40, 50, 60, 70, 80, ...
By examining the lists, we observe that the smallest multiple common to both 7 and 10 is 70. Therefore, the LCM of 7 and 10 is 70.
While simple for small numbers, this method becomes less efficient for larger numbers or when dealing with more than two numbers.
Method 2: Prime Factorization
This method provides a more systematic and efficient approach, especially for larger numbers. It relies on expressing each number as a product of its prime factors.
- Prime factorization of 7: 7 is a prime number, so its prime factorization is simply 7.
- Prime factorization of 10: 10 = 2 x 5
To find the LCM using prime factorization, we identify the highest power of each prime factor present in the factorizations:
- The prime factors are 2, 5, and 7.
- The highest power of 2 is 2¹ = 2.
- The highest power of 5 is 5¹ = 5.
- The highest power of 7 is 7¹ = 7.
Multiplying these highest powers together gives us the LCM: 2 x 5 x 7 = 70.
This method is more efficient because it doesn't require listing all multiples. It works equally well for larger numbers and multiple numbers.
Method 3: Using the Greatest Common Divisor (GCD)
The LCM and the greatest common divisor (GCD) are intimately related. The product of the LCM and GCD of two numbers is equal to the product of the two numbers. This relationship provides another method for calculating the LCM.
First, we need to find the GCD of 7 and 10. Since 7 is a prime number and 10 is not divisible by 7, their GCD is 1.
Using the formula: LCM(a, b) * GCD(a, b) = a * b, where 'a' and 'b' are the two numbers.
Substituting the values: LCM(7, 10) * 1 = 7 * 10
Solving for LCM(7, 10): LCM(7, 10) = 70
This method leverages the relationship between LCM and GCD, offering an alternative approach, especially useful when the GCD is easily identifiable.
Method 4: Using the Formula for Two Numbers
For two numbers 'a' and 'b', a more direct formula exists:
LCM(a, b) = (|a * b|) / GCD(a, b)
Where |a * b| represents the absolute value of the product of a and b. Again, we need the GCD. Since GCD(7, 10) = 1:
LCM(7, 10) = (|7 * 10|) / 1 = 70
This formula directly calculates the LCM, avoiding the need for multiple steps.
Explanation of the Methods: A Deeper Dive
The effectiveness of each method stems from fundamental number theory concepts. The listing multiples method is intuitive but inefficient for larger numbers. The prime factorization method relies on the unique prime factorization theorem, which states that every integer greater than 1 can be represented as a unique product of prime numbers. This ensures accuracy and efficiency. The GCD method and the formula method exploit the inherent relationship between LCM and GCD, providing alternative and often more efficient pathways to the solution. Understanding the GCD is crucial, as it represents the largest number that divides both numbers without leaving a remainder. Efficient algorithms exist for computing GCD, like the Euclidean algorithm, which significantly speeds up the LCM calculation for very large numbers.
Why is finding the LCM important? Real-world applications.
Beyond academic exercises, the LCM finds practical application in various scenarios:
- Scheduling: Imagine two buses leave a station at different intervals. One bus leaves every 7 minutes, and another every 10 minutes. The LCM (70 minutes) determines when both buses will depart simultaneously again.
- Fraction Operations: When adding or subtracting fractions, finding the LCM of the denominators helps find the least common denominator (LCD), simplifying the calculation. For example, adding 1/7 and 1/10 requires finding the LCD, which is the LCM of 7 and 10 (70).
- Cyclic Events: Many real-world phenomena are cyclic. Understanding LCM helps predict when these cycles will coincide. This is useful in areas like astronomy (planetary alignments), engineering (machine synchronization), and even music (harmonic intervals).
- Modular Arithmetic: LCM plays a vital role in modular arithmetic, a branch of number theory with applications in cryptography and computer science.
Frequently Asked Questions (FAQ)
- Q: What if I have more than two numbers? The prime factorization method extends easily to multiple numbers. Find the prime factorization of each number, and then take the highest power of each prime factor present across all factorizations. Multiply these highest powers to obtain the LCM.
- Q: Is there a single "best" method? The optimal method depends on the numbers involved. For small numbers, listing multiples is fine. For larger numbers, prime factorization or the GCD-based methods are more efficient.
- Q: What if the numbers are very large? For extremely large numbers, specialized algorithms, like the Euclidean algorithm for GCD computation, become crucial for efficient calculation. Computer programs are commonly used for these calculations.
- Q: Can the LCM be greater than the product of the two numbers? No, the LCM of two numbers is always less than or equal to the product of the two numbers.
Conclusion: Mastering the LCM
Finding the least common multiple is more than just a mathematical exercise; it's a fundamental concept with wide-ranging applications. Mastering different methods – listing multiples, prime factorization, using the GCD – equips you with the tools to tackle various problems efficiently and understand the underlying mathematical principles. Understanding the LCM unlocks a deeper appreciation for number theory and its relevance in solving real-world problems. By understanding these methods and their underlying principles, you'll be well-prepared to handle LCM calculations for any numbers, no matter how large or complex they may be. Remember, the key is to choose the most efficient method based on the numbers involved and your understanding of the underlying concepts.
Latest Posts
Latest Posts
-
What Is Equal To 3 2
Sep 16, 2025
-
26000 Sq Ft To Acres
Sep 16, 2025
-
Convert 145 Lbs To Kg
Sep 16, 2025
-
1 200 Minutes In Hours
Sep 16, 2025
-
Lcm Of 12 And 11
Sep 16, 2025
Related Post
Thank you for visiting our website which covers about Lcm For 7 And 10 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.