Lcm Of 12 And 13
saludintensiva
Sep 09, 2025 · 6 min read
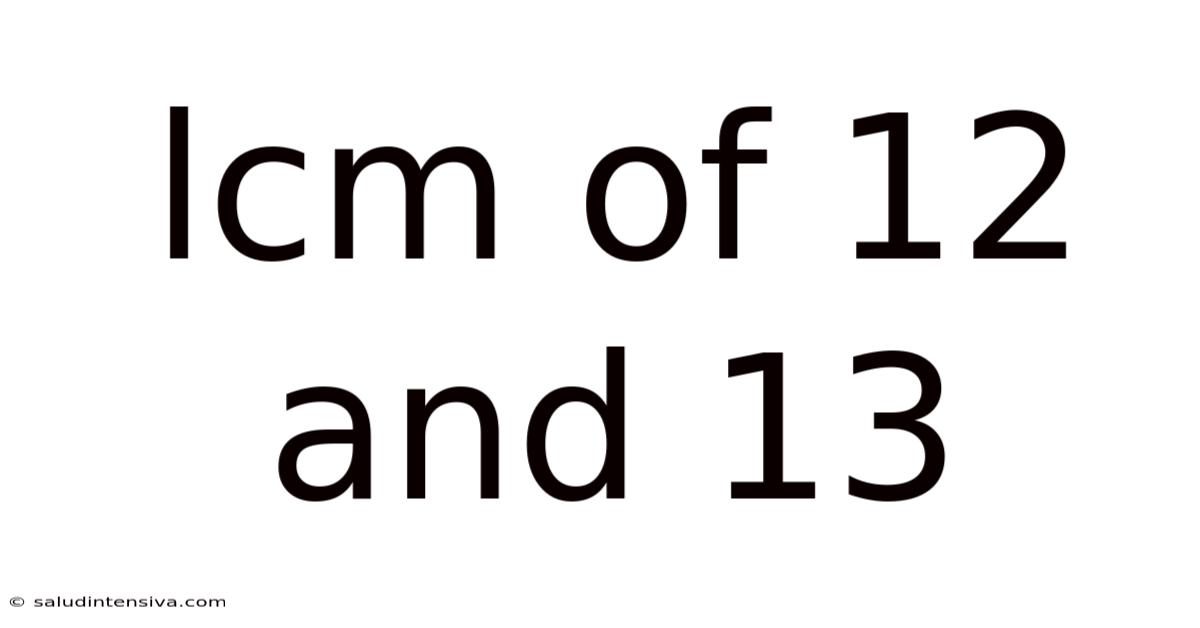
Table of Contents
Finding the Least Common Multiple (LCM) of 12 and 13: A Deep Dive
Finding the least common multiple (LCM) might seem like a simple arithmetic task, but understanding the underlying concepts and different methods for calculating it can be incredibly valuable for grasping more advanced mathematical principles. This article will explore the LCM of 12 and 13 in detail, explaining various approaches and providing a deeper understanding of the concept itself. We will go beyond a simple answer, exploring the theoretical foundations and practical applications of LCM calculations.
Introduction: Understanding Least Common Multiples
The least common multiple (LCM) of two or more integers is the smallest positive integer that is divisible by all the integers. Think of it as the smallest number that contains all the integers as factors. Understanding LCM is crucial in various mathematical contexts, including simplifying fractions, solving problems involving time intervals, and even in advanced areas like abstract algebra. In this article, we'll focus on the specific case of finding the LCM of 12 and 13. While seemingly straightforward, this example provides an excellent opportunity to solidify understanding of the core principles.
Method 1: Listing Multiples
The most intuitive method to find the LCM is by listing the multiples of each number until a common multiple is found. Let's do this for 12 and 13:
- Multiples of 12: 12, 24, 36, 48, 60, 72, 84, 96, 108, 120, 132, 144, 156...
- Multiples of 13: 13, 26, 39, 52, 65, 78, 91, 104, 117, 130, 143, 156...
Notice that the smallest number that appears in both lists is 156. Therefore, the LCM of 12 and 13 is 156. This method is straightforward for smaller numbers, but it becomes less efficient as the numbers get larger.
Method 2: Prime Factorization
A more efficient and systematic approach involves using prime factorization. This method relies on breaking down each number into its prime factors. Remember, a prime number is a whole number greater than 1 that has only two divisors: 1 and itself.
- Prime factorization of 12: 2² × 3
- Prime factorization of 13: 13 (13 is a prime number)
To find the LCM using prime factorization, we take the highest power of each prime factor present in either factorization and multiply them together:
LCM(12, 13) = 2² × 3 × 13 = 4 × 3 × 13 = 12 × 13 = 156
This method is generally preferred for larger numbers because it's more systematic and avoids the need to list out potentially many multiples. It also provides a deeper understanding of the numbers' structure.
Method 3: Using the Greatest Common Divisor (GCD)
The LCM and the greatest common divisor (GCD) are closely related. The GCD is the largest positive integer that divides both numbers without leaving a remainder. There's a useful formula connecting the LCM and GCD:
LCM(a, b) = (|a × b|) / GCD(a, b)
Where |a × b| represents the absolute value of the product of a and b.
Let's find the GCD of 12 and 13 using the Euclidean algorithm:
- Divide the larger number (13) by the smaller number (12): 13 ÷ 12 = 1 with a remainder of 1.
- Replace the larger number with the smaller number (12) and the smaller number with the remainder (1).
- Repeat: 12 ÷ 1 = 12 with a remainder of 0.
- The GCD is the last non-zero remainder, which is 1.
Therefore, GCD(12, 13) = 1. Now we can use the formula:
LCM(12, 13) = (12 × 13) / 1 = 156
This method elegantly connects the concepts of LCM and GCD, highlighting their inherent relationship.
Why is the LCM Important? Real-World Applications
Understanding LCM extends beyond the realm of abstract mathematics and finds practical applications in various scenarios:
-
Scheduling and Time Management: Imagine two buses arrive at a stop at different intervals. One bus arrives every 12 minutes, and the other every 13 minutes. To find when both buses arrive at the stop simultaneously, you need to find the LCM of 12 and 13, which is 156 minutes (or 2 hours and 36 minutes).
-
Fraction Operations: When adding or subtracting fractions with different denominators, you need to find the LCM of the denominators to find a common denominator. This simplifies the calculation and provides an accurate result.
-
Project Management: In project planning, LCM helps in coordinating tasks that have different completion cycles. For example, if one task takes 12 days and another takes 13 days, the LCM (156 days) indicates the shortest time until both tasks can be completed simultaneously, allowing for efficient resource allocation.
Frequently Asked Questions (FAQ)
-
Q: Is the LCM always greater than or equal to the larger of the two numbers?
- A: Yes, the LCM is always greater than or equal to the largest number among the given set. This is because the LCM must be divisible by all the numbers in the set.
-
Q: What if the two numbers are the same?
- A: If the two numbers are identical, the LCM is simply the number itself. For example, LCM(5, 5) = 5.
-
Q: Can the LCM be found for more than two numbers?
- A: Yes, the same methods (prime factorization and GCD approach) can be extended to find the LCM of three or more numbers. You simply extend the prime factorization to include all the numbers and use the highest power of each prime factor present. For the GCD method, you would need to iteratively find the GCD of pairs of numbers and then continue to find the GCD until you get a single result.
-
Q: Are there any shortcuts for finding the LCM if the numbers share a common factor?
- A: While prime factorization already accounts for common factors, noticing common factors can simplify the calculation. If you recognize that the numbers share a common factor, you can factor it out before applying the methods above and then multiply the result by that common factor.
Conclusion:
Finding the LCM of 12 and 13, while seemingly a basic arithmetic exercise, illustrates fundamental mathematical concepts with far-reaching applications. We've explored three distinct methods – listing multiples, prime factorization, and using the GCD – each offering a unique perspective and enhancing understanding. The LCM isn't just a theoretical construct; it's a practical tool employed in various fields, highlighting the importance of grasping these fundamental mathematical concepts. Understanding the LCM helps build a stronger foundation for tackling more complex mathematical problems in the future. By mastering these concepts, you not only solve specific numerical problems but also develop a deeper appreciation for the interconnectedness of mathematical ideas.
Latest Posts
Latest Posts
-
6 Out Of 9 Percentage
Sep 10, 2025
-
2to The Power Of 4
Sep 10, 2025
-
110 Degrees F In Celsius
Sep 10, 2025
-
Random Number Wheel 1 50
Sep 10, 2025
-
17 100 As A Decimal
Sep 10, 2025
Related Post
Thank you for visiting our website which covers about Lcm Of 12 And 13 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.