Lcm Of 13 And 4
saludintensiva
Sep 13, 2025 · 6 min read
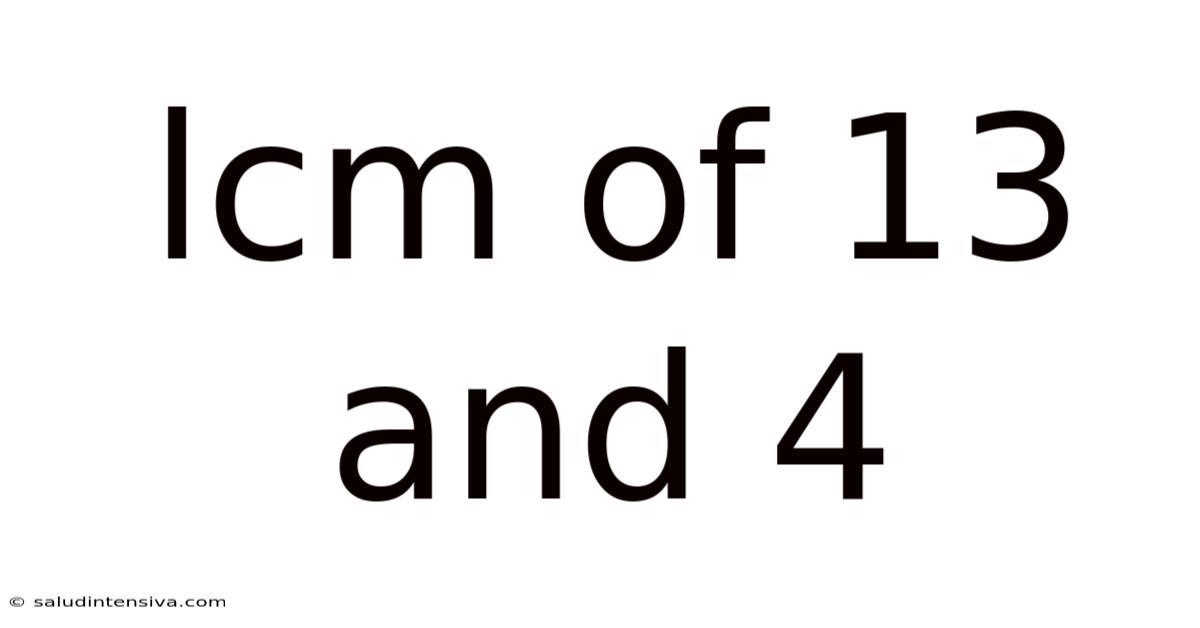
Table of Contents
Finding the Least Common Multiple (LCM) of 13 and 4: A Comprehensive Guide
The least common multiple (LCM) is a fundamental concept in mathematics, particularly crucial in areas like fractions, algebra, and even music theory. Understanding how to find the LCM is essential for simplifying expressions, solving equations, and understanding rhythmic patterns. This article will provide a thorough explanation of how to find the LCM of 13 and 4, exploring various methods and delving into the underlying mathematical principles. We'll cover different approaches, address common misconceptions, and answer frequently asked questions, ensuring you gain a complete understanding of this important concept.
Understanding Least Common Multiple (LCM)
Before we tackle the specific example of finding the LCM of 13 and 4, let's define the term. The least common multiple (LCM) of two or more integers is the smallest positive integer that is a multiple of all the integers. In simpler terms, it's the smallest number that both (or all) of your given numbers can divide into evenly. For example, the multiples of 2 are 2, 4, 6, 8, 10, and so on. The multiples of 3 are 3, 6, 9, 12, 15, and so on. The least common multiple of 2 and 3 is 6 because it is the smallest number that appears in both lists.
Method 1: Listing Multiples
This is the most straightforward method, especially for smaller numbers like 13 and 4. We simply list out the multiples of each number until we find the smallest multiple that is common to both.
- Multiples of 13: 13, 26, 39, 52, 65, 78, 91, 104, 117, 130...
- Multiples of 4: 4, 8, 12, 16, 20, 24, 28, 32, 36, 40, 44, 48, 52, 56, 60, 64, 68, 72, 76, 80, 84, 88, 92, 96, 100, 104...
Notice that 52 and 104 appear in both lists. However, 52 is the smallest number common to both lists. Therefore, the LCM of 13 and 4 is 52.
Method 2: Prime Factorization
This method is more efficient for larger numbers and provides a deeper understanding of the underlying mathematical principles. It involves breaking down each number into its prime factors. Prime factors are numbers that are only divisible by 1 and themselves (e.g., 2, 3, 5, 7, 11, etc.).
-
Prime factorization of 13: 13 is a prime number, so its prime factorization is simply 13.
-
Prime factorization of 4: 4 = 2 x 2 = 2²
-
Finding the LCM: To find the LCM using prime factorization, we take the highest power of each prime factor present in either factorization and multiply them together. In this case, we have a prime factor of 2 (with the highest power of 2²) and a prime factor of 13 (with a power of 1).
Therefore, LCM(13, 4) = 2² x 13 = 4 x 13 = 52
Method 3: Using the Formula (LCM and GCD)
The least common multiple (LCM) and the greatest common divisor (GCD) are closely related. There's a formula that connects them:
LCM(a, b) x GCD(a, b) = a x b
Where 'a' and 'b' are the two numbers.
-
Find the GCD (Greatest Common Divisor): The greatest common divisor is the largest number that divides both numbers evenly. In the case of 13 and 4, their GCD is 1 because 1 is the only number that divides both 13 and 4 without leaving a remainder.
-
Apply the formula: We know that:
LCM(13, 4) x GCD(13, 4) = 13 x 4 LCM(13, 4) x 1 = 52 LCM(13, 4) = 52
Method 4: Using the Euclidean Algorithm (for GCD and then the formula)
The Euclidean Algorithm is an efficient method for finding the greatest common divisor (GCD) of two numbers. Once we have the GCD, we can use the formula above to find the LCM.
- Euclidean Algorithm:
- Divide the larger number (13) by the smaller number (4): 13 = 3 x 4 + 1
- The remainder is 1. If the remainder were 0, the smaller number would be the GCD.
- Since the remainder is 1, the GCD is 1.
- Apply the formula (as in Method 3): LCM(13, 4) = (13 x 4) / GCD(13, 4) = 52 / 1 = 52
Therefore, the LCM of 13 and 4 is 52.
Why is Understanding LCM Important?
The LCM has numerous applications across various fields:
-
Fraction Operations: Finding the LCM of denominators is crucial when adding or subtracting fractions. It allows you to find a common denominator, simplifying the calculation process.
-
Scheduling Problems: Imagine two buses that leave a station at different intervals. The LCM helps determine when the buses will depart together again.
-
Rhythmic Patterns in Music: In music theory, the LCM helps determine the least common period of repeating rhythmic patterns.
-
Algebra and Number Theory: LCM plays a significant role in simplifying algebraic expressions and solving equations involving multiples.
Frequently Asked Questions (FAQ)
Q1: What if one of the numbers is 0?
A1: The LCM of any number and 0 is undefined. Zero is a multiple of every number, leading to an infinite number of common multiples.
Q2: Can the LCM of two numbers be one of the numbers?
A2: Yes, if one number is a multiple of the other, the LCM will be the larger number. For example, the LCM of 6 and 3 is 6.
Q3: Is there a limit to how many numbers you can find the LCM for?
A3: No, the concept of LCM extends to any number of integers. The methods discussed can be adapted to find the LCM of three or more numbers. For example, to find the LCM of three numbers a, b, and c, you can first find the LCM of a and b, and then find the LCM of the result and c.
Q4: What's the difference between LCM and GCD?
A4: The LCM (Least Common Multiple) is the smallest number that is a multiple of all given numbers, while the GCD (Greatest Common Divisor) is the largest number that divides all given numbers evenly. They are inversely related; as one increases, the other generally decreases.
Conclusion
Finding the LCM of 13 and 4, while seemingly simple, provides a foundational understanding of this important mathematical concept. We've explored multiple methods—listing multiples, prime factorization, using the LCM/GCD formula, and the Euclidean algorithm—demonstrating the versatility and efficiency of different approaches. Understanding the LCM is not just about solving mathematical problems; it's about grasping a fundamental principle that extends its application into various fields, highlighting its significance in mathematics, music, and everyday problem-solving. Remember, the key is to choose the method most comfortable and efficient for the given numbers. Practice is crucial for mastering this skill.
Latest Posts
Latest Posts
-
Greatest Common Factor Of 13
Sep 14, 2025
-
7000 Sq Ft To Acres
Sep 14, 2025
-
Pressure Force And Area Formula
Sep 14, 2025
-
Gcf Of 32 And 45
Sep 14, 2025
-
What Time Is 15 54
Sep 14, 2025
Related Post
Thank you for visiting our website which covers about Lcm Of 13 And 4 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.