Lcm Of 14 And 49
saludintensiva
Sep 13, 2025 · 6 min read
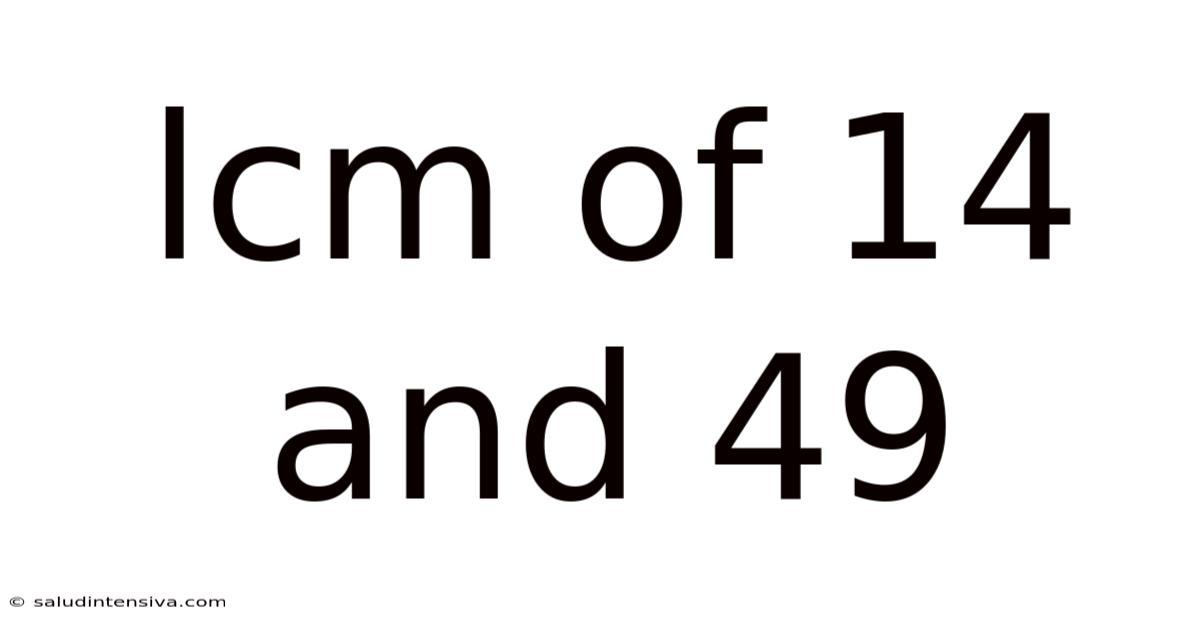
Table of Contents
Finding the LCM of 14 and 49: A Comprehensive Guide
Finding the least common multiple (LCM) is a fundamental concept in mathematics, particularly useful in simplifying fractions, solving problems involving cycles, and understanding rhythmic patterns. This article will comprehensively explore how to find the LCM of 14 and 49, covering various methods and delving into the underlying mathematical principles. We'll move beyond simply finding the answer and explore the "why" behind the techniques, solidifying your understanding of LCM and its applications.
Understanding Least Common Multiple (LCM)
Before we dive into calculating the LCM of 14 and 49, let's establish a clear understanding of what LCM actually means. The least common multiple of two or more numbers is the smallest positive integer that is a multiple of all the numbers. In simpler terms, it's the smallest number that all the given numbers can divide into evenly without leaving a remainder.
For example, if we consider the numbers 2 and 3, their multiples are:
- Multiples of 2: 2, 4, 6, 8, 10, 12, 14, 16…
- Multiples of 3: 3, 6, 9, 12, 15, 18…
The common multiples of 2 and 3 are 6, 12, 18, and so on. The least common multiple is 6.
Method 1: Listing Multiples
This is the most straightforward method, especially for smaller numbers like 14 and 49. We list the multiples of each number until we find the smallest common multiple.
- Multiples of 14: 14, 28, 42, 56, 70, 84, 98, 112, 126, 140…
- Multiples of 49: 49, 98, 147, 196…
By comparing the lists, we can see that the smallest number that appears in both lists is 98. Therefore, the LCM of 14 and 49 is 98.
This method is effective for smaller numbers but can become cumbersome and time-consuming for larger numbers. Let's explore more efficient methods.
Method 2: Prime Factorization
Prime factorization is a powerful technique for finding the LCM of any set of numbers, regardless of their size. It involves breaking down each number into its prime factors – the prime numbers that multiply together to make the original number.
Let's find the prime factorization of 14 and 49:
- 14: 2 x 7
- 49: 7 x 7 or 7²
Now, to find the LCM, we take the highest power of each prime factor present in either factorization and multiply them together:
LCM(14, 49) = 2 x 7² = 2 x 49 = 98
This method is more efficient than listing multiples, particularly when dealing with larger numbers, as it provides a systematic approach to finding the LCM. Understanding prime factorization is a fundamental skill in number theory and has wide-ranging applications beyond just finding LCMs.
Method 3: Using the Formula (LCM and GCD Relationship)
The LCM and the greatest common divisor (GCD) of two numbers are intimately related. There's a formula that connects them:
LCM(a, b) x GCD(a, b) = a x b
Where 'a' and 'b' are the two numbers.
First, let's find the GCD of 14 and 49 using the Euclidean algorithm or prime factorization:
- Prime Factorization Method: The prime factors of 14 are 2 and 7. The prime factors of 49 are 7 and 7. The only common prime factor is 7, so the GCD(14, 49) = 7.
Now, we can use the formula:
LCM(14, 49) x GCD(14, 49) = 14 x 49 LCM(14, 49) x 7 = 686 LCM(14, 49) = 686 / 7 = 98
This method elegantly connects the concepts of LCM and GCD, demonstrating their inherent relationship. It’s a powerful tool for efficiently calculating LCMs, especially when the GCD is easily determined.
Method 4: Visual Representation using Venn Diagrams
Venn diagrams can provide a visual and intuitive understanding of the relationship between LCM and GCD. Let's represent the prime factorization of 14 and 49 in a Venn diagram:
- 14: 2 and 7
- 49: 7 and 7
The Venn diagram would show a circle for 14 containing 2 and 7, and a circle for 49 containing two 7s. The overlapping region represents the GCD (7 in this case). The LCM is found by multiplying all the unique prime factors, taking the highest power if a factor is repeated. In this case, it's 2 x 7 x 7 = 98.
This method offers a visual approach to understanding the concept, particularly helpful for students who benefit from visual learning.
Applications of LCM
The concept of LCM has numerous real-world applications:
- Scheduling: Imagine two buses arrive at a bus stop at different intervals. The LCM helps determine when both buses will arrive at the stop simultaneously.
- Fraction Addition/Subtraction: Finding a common denominator when adding or subtracting fractions involves finding the LCM of the denominators.
- Rhythmic Patterns: In music, LCM is used to determine when different rhythmic patterns will coincide.
- Gear Ratios: In mechanics, LCM is crucial in calculating gear ratios and synchronizing rotating components.
- Calendars: Determining when certain dates will coincide (like a specific day of the week falling on a specific date in different years) often involves using LCM concepts.
Frequently Asked Questions (FAQ)
-
Q: What if the numbers have no common factors? A: If the numbers are relatively prime (i.e., their GCD is 1), then their LCM is simply the product of the two numbers.
-
Q: Can I use this method for more than two numbers? A: Yes, the prime factorization method can be extended to find the LCM of more than two numbers. You would find the prime factorization of each number, and then take the highest power of each prime factor present in any of the factorizations.
-
Q: Is there a quickest method to find LCM? A: The quickest method depends on the numbers. For small numbers, listing multiples might be fastest. For larger numbers, prime factorization is generally more efficient. Using the LCM-GCD relationship can also be very efficient if the GCD is easily calculated.
-
Q: Why is the LCM important in fraction operations? A: To add or subtract fractions, you need a common denominator. The LCM of the denominators provides the smallest common denominator, making the calculation simpler and resulting in a fraction in its simplest form.
Conclusion
Finding the LCM of 14 and 49, as demonstrated through various methods, is more than just a simple calculation. It's an opportunity to grasp fundamental mathematical concepts like prime factorization, the relationship between LCM and GCD, and the practical applications of these concepts in diverse fields. Understanding these methods empowers you to tackle more complex LCM problems and appreciate the elegance and utility of number theory. The ability to find the LCM efficiently is a valuable skill applicable in various mathematical contexts and real-world scenarios. Remember to choose the method that best suits the numbers involved and your comfort level with different mathematical techniques.
Latest Posts
Latest Posts
-
2 To The Power 7
Sep 13, 2025
-
27 Degrees F To C
Sep 13, 2025
-
Lcm Of 17 And 8
Sep 13, 2025
-
2 16 As A Percent
Sep 13, 2025
-
Gcf For 30 And 75
Sep 13, 2025
Related Post
Thank you for visiting our website which covers about Lcm Of 14 And 49 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.