Lcm Of 15 And 30
saludintensiva
Sep 16, 2025 · 6 min read
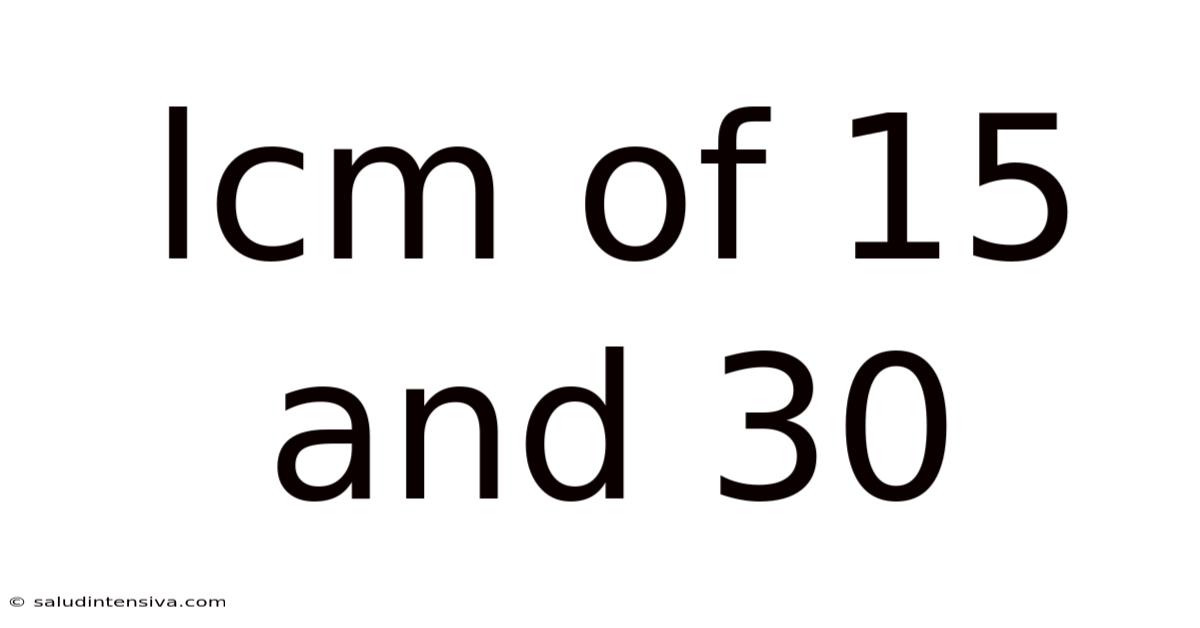
Table of Contents
Unveiling the Least Common Multiple (LCM) of 15 and 30: A Deep Dive
Finding the Least Common Multiple (LCM) might seem like a simple arithmetic task, especially when dealing with smaller numbers like 15 and 30. However, understanding the underlying concepts and various methods for calculating the LCM is crucial for grasping more advanced mathematical concepts later on. This article will not only show you how to find the LCM of 15 and 30 but also explore the theoretical foundations, different calculation methods, and real-world applications of this fundamental concept. We'll delve deep, ensuring a thorough understanding, suitable for students and anyone curious about the beauty of mathematics.
Introduction to Least Common Multiple (LCM)
The Least Common Multiple (LCM) of two or more integers is the smallest positive integer that is divisible by all the integers. In simpler terms, it's the smallest number that contains all the numbers you're considering as factors. Understanding the LCM is essential in various mathematical operations, including simplifying fractions, solving problems involving ratios and proportions, and even in more advanced fields like abstract algebra. This article focuses on the practical calculation of the LCM, using the example of 15 and 30, but also explains the broader significance of this concept.
Method 1: Listing Multiples
This is the most straightforward method, particularly useful for smaller numbers. Let's find the LCM of 15 and 30 using this approach.
First, list the multiples of 15: 15, 30, 45, 60, 75, 90, 105...
Next, list the multiples of 30: 30, 60, 90, 120...
Now, compare the two lists. The smallest number that appears in both lists is 30. Therefore, the LCM of 15 and 30 is 30.
This method works well for small numbers, but it becomes increasingly inefficient as the numbers get larger. Imagine trying to find the LCM of 147 and 252 using this method; it would be quite tedious!
Method 2: Prime Factorization
This method is more efficient and works for larger numbers as well. It involves breaking down each number into its prime factors. Prime numbers are numbers greater than 1 that are only divisible by 1 and themselves (e.g., 2, 3, 5, 7, 11...).
Let's find the prime factorization of 15 and 30:
- 15 = 3 x 5
- 30 = 2 x 3 x 5
Now, to find the LCM, we take the highest power of each prime factor present in either factorization and multiply them together.
In this case, the prime factors are 2, 3, and 5. The highest power of 2 is 2¹ (from 30), the highest power of 3 is 3¹ (from both 15 and 30), and the highest power of 5 is 5¹ (from both 15 and 30).
Therefore, LCM(15, 30) = 2¹ x 3¹ x 5¹ = 2 x 3 x 5 = 30
Method 3: Using the Greatest Common Divisor (GCD)
The LCM and the Greatest Common Divisor (GCD) are intimately related. The GCD is the largest number that divides both integers without leaving a remainder. There's a handy formula connecting the LCM and GCD:
LCM(a, b) x GCD(a, b) = a x b
Let's find the GCD of 15 and 30 using the prime factorization method:
- 15 = 3 x 5
- 30 = 2 x 3 x 5
The common prime factors are 3 and 5. Therefore, the GCD(15, 30) = 3 x 5 = 15.
Now, using the formula:
LCM(15, 30) = (15 x 30) / GCD(15, 30) = (15 x 30) / 15 = 30
Method 4: Listing Factors (for smaller numbers)
This method works well for smaller numbers and provides a visual understanding of the relationship between factors and multiples. Let's list the factors of 15 and 30:
Factors of 15: 1, 3, 5, 15 Factors of 30: 1, 2, 3, 5, 6, 10, 15, 30
Notice that 15 is a factor of 30. If one number is a factor of the other, the larger number is the LCM. Therefore, the LCM(15, 30) = 30. This is a shortcut, but be cautious; it only works when one number is a factor of the other.
The Significance of LCM in Real-World Applications
The LCM isn't just a theoretical concept confined to textbooks. It has practical applications in various real-world scenarios:
-
Scheduling: Imagine two buses that leave a station at different intervals. One bus leaves every 15 minutes, and the other leaves every 30 minutes. The LCM helps determine when both buses will depart simultaneously again. In this case, the LCM(15, 30) = 30, meaning they'll leave together every 30 minutes.
-
Fraction Operations: When adding or subtracting fractions, you need a common denominator. This common denominator is the LCM of the denominators. For example, to add 1/15 and 1/30, you'd find the LCM of 15 and 30 (which is 30), and then convert the fractions to have a denominator of 30 before adding.
-
Gear Ratios: In mechanics, gear ratios are often expressed as ratios of integers. The LCM can help determine the least number of rotations required for the gears to return to their original positions.
-
Project Management: In project planning, tasks might have different durations. The LCM can help determine the shortest interval after which all tasks will be completed simultaneously, enabling better synchronization and resource allocation.
Understanding the Mathematical Basis: Divisibility Rules
The concept of divisibility plays a crucial role in understanding LCM. A number is divisible by another if it leaves no remainder when divided. Knowing divisibility rules (e.g., a number is divisible by 3 if the sum of its digits is divisible by 3) can simplify the process of finding prime factors and the LCM.
Frequently Asked Questions (FAQ)
Q1: What if I have more than two numbers? How do I find the LCM?
A1: The same methods apply. For prime factorization, you consider all prime factors present in the factorizations of all numbers. For the GCD method, you can use iterative approaches to find the GCD of multiple numbers and then apply the LCM formula accordingly.
Q2: Is there a formula for finding the LCM of any number of integers?
A2: While there isn't a single concise formula for an arbitrary number of integers like there is for two, the prime factorization method remains effective. You simply extend the process to include all the given integers and their prime factors.
Q3: What if the numbers are relatively prime (their GCD is 1)?
A3: If the GCD of two numbers is 1, their LCM is simply their product. For example, the LCM of 15 and 28 (GCD =1) is 15 * 28 = 420.
Q4: Can I use a calculator to find the LCM?
A4: Many scientific calculators and online calculators have built-in functions for calculating the LCM.
Conclusion: Mastering the LCM
Understanding the Least Common Multiple is a fundamental step in mastering arithmetic and progressing to more advanced mathematical concepts. This article has explored various methods for calculating the LCM, focusing on the example of 15 and 30. While the listing multiples method is simple for smaller numbers, prime factorization and the GCD method provide more efficient approaches for larger numbers. Remember that the LCM is not just a theoretical concept; it has practical applications in diverse fields, from scheduling to engineering. By grasping the principles and practicing different methods, you can confidently tackle LCM problems and appreciate the beauty and usefulness of this mathematical tool. So, embrace the challenge, practice diligently, and unlock the power of the LCM!
Latest Posts
Latest Posts
-
Convert Mm To Sq Ft
Sep 16, 2025
-
Lcm Of 25 30 35
Sep 16, 2025
-
How Much Is 400 Minutes
Sep 16, 2025
-
9148 Sq Ft To Acres
Sep 16, 2025
-
Surface Area Prisms And Pyramids
Sep 16, 2025
Related Post
Thank you for visiting our website which covers about Lcm Of 15 And 30 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.