Lcm Of 20 And 10
saludintensiva
Sep 17, 2025 · 6 min read
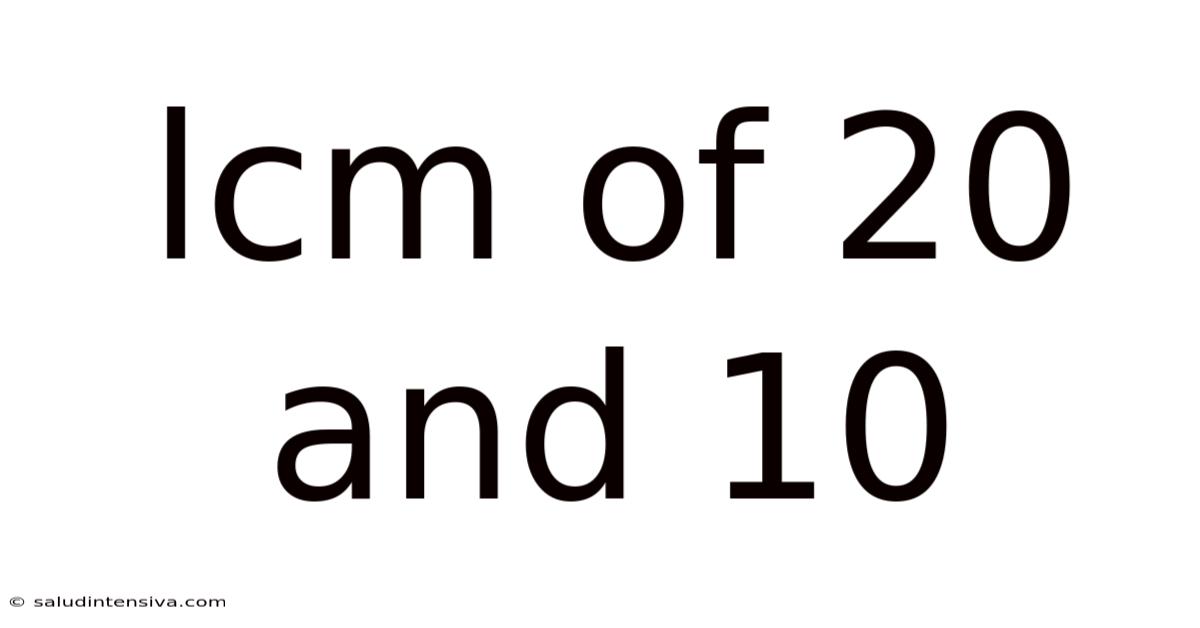
Table of Contents
Understanding the Least Common Multiple (LCM) of 20 and 10
Finding the Least Common Multiple (LCM) might seem like a simple arithmetic task, especially when dealing with smaller numbers like 20 and 10. However, understanding the underlying concepts and different methods for calculating the LCM provides a strong foundation for tackling more complex problems in mathematics, particularly in areas like algebra, fractions, and even programming. This article will delve deep into the LCM of 20 and 10, explaining the various methods available, providing a solid theoretical basis, and addressing frequently asked questions. We'll move beyond simply stating the answer to truly understanding why the answer is what it is.
What is the Least Common Multiple (LCM)?
Before we jump into calculating the LCM of 20 and 10, let's define what it means. The Least Common Multiple (LCM) of two or more integers is the smallest positive integer that is a multiple of all the integers. In simpler terms, it's the smallest number that both (or all) of your numbers can divide into evenly without leaving a remainder.
Imagine you have two gears, one with 20 teeth and another with 10 teeth. The LCM represents the number of rotations needed for both gears to return to their starting positions simultaneously. This analogy helps visualize the practical application of the concept beyond abstract mathematical definitions.
Methods for Finding the LCM of 20 and 10
There are several ways to determine the LCM, each with its own advantages and disadvantages. Let's explore the most common methods using the example of 20 and 10:
1. Listing Multiples Method
This is the most straightforward approach, especially for smaller numbers. We list the multiples of each number until we find the smallest common multiple.
- Multiples of 10: 10, 20, 30, 40, 50, 60…
- Multiples of 20: 20, 40, 60, 80, 100…
By comparing the lists, we can clearly see that the smallest number appearing in both lists is 20. Therefore, the LCM of 20 and 10 is 20.
This method is simple but becomes less efficient as the numbers get larger. Listing all the multiples can be time-consuming and prone to errors.
2. Prime Factorization Method
This method utilizes the prime factorization of each number. A prime number is a whole number greater than 1 that has only two divisors: 1 and itself (e.g., 2, 3, 5, 7, 11).
- Prime factorization of 10: 2 x 5
- Prime factorization of 20: 2 x 2 x 5 or 2² x 5
The process involves identifying the highest power of each prime factor present in the factorizations.
- Highest power of 2: 2² = 4
- Highest power of 5: 5¹ = 5
Multiply these highest powers together: 2² x 5 = 20. Therefore, the LCM of 20 and 10 is 20.
This method is more efficient for larger numbers because it avoids listing all multiples. It's also a more fundamental method, connecting directly to the core concept of prime numbers and their role in number theory.
3. Greatest Common Divisor (GCD) Method
The LCM and the Greatest Common Divisor (GCD) are closely related. The GCD is the largest number that divides both integers without leaving a remainder. We can use the following formula:
LCM(a, b) = (|a x b|) / GCD(a, b)
where |a x b| represents the absolute value of the product of a and b.
First, let's find the GCD of 20 and 10. We can use the Euclidean algorithm for this:
- Divide the larger number (20) by the smaller number (10): 20 ÷ 10 = 2 with a remainder of 0.
- Since the remainder is 0, the GCD is the smaller number, which is 10.
Now, we can apply the formula:
LCM(20, 10) = (|20 x 10|) / GCD(20, 10) = 200 / 10 = 20
This method is efficient, particularly for larger numbers, as finding the GCD is often computationally less demanding than directly calculating the LCM. The Euclidean algorithm is a particularly robust and efficient way to compute the GCD.
A Deeper Dive into the Concepts
Understanding the relationship between LCM and GCD is crucial. They are inversely proportional in a sense. As the GCD increases, the LCM decreases, and vice versa. This is because a larger common divisor means that the numbers share more factors, reducing the need for a larger multiple to encompass all factors.
The prime factorization method highlights the fundamental building blocks of numbers. Every integer can be uniquely expressed as a product of prime numbers (Fundamental Theorem of Arithmetic). This makes it a powerful tool not only for finding the LCM but also for understanding the structure and properties of numbers.
Applications of LCM
The LCM has applications beyond simple arithmetic exercises. Here are a few examples:
- Scheduling: Imagine two buses depart from a station at different intervals. The LCM helps determine when both buses will depart simultaneously again.
- Fraction Operations: When adding or subtracting fractions with different denominators, finding the LCM of the denominators is crucial for finding a common denominator.
- Music Theory: The LCM is used in music to determine the least common period for rhythmic patterns.
- Computer Programming: The concept of LCM is used in algorithms related to scheduling and resource management.
Frequently Asked Questions (FAQ)
Q: What if the numbers have no common factors other than 1?
A: If the numbers are relatively prime (meaning their GCD is 1), then their LCM is simply the product of the two numbers. For example, LCM(15, 4) = 15 x 4 = 60 because 15 and 4 share no common factors other than 1.
Q: Can I find the LCM of more than two numbers?
A: Yes, you can extend the methods discussed above to find the LCM of multiple numbers. For the prime factorization method, you would consider the highest power of each prime factor present in the factorization of all the numbers. For the GCD method, you would need to iteratively compute the LCM of pairs of numbers.
Q: Is there a formula to directly calculate the LCM for any two numbers?
A: While there isn't a single, direct formula that avoids using the GCD or prime factorization, the formula involving the GCD provides a computationally efficient alternative to listing multiples.
Conclusion
Finding the Least Common Multiple of 20 and 10, which is 20, is just the starting point. This article has taken you beyond a simple calculation to understand the underlying mathematical concepts and the various methods employed. Mastering the LCM is not just about memorizing formulas; it's about understanding the structure of numbers, prime factorization, and the interconnectedness of mathematical concepts. This understanding is invaluable for tackling more complex mathematical problems and applying these concepts to real-world situations. From scheduling to music theory to programming, the LCM plays a significant, albeit often unseen, role in various fields. Therefore, the seemingly simple question of "what is the LCM of 20 and 10?" unlocks a much wider understanding of number theory and its practical applications.
Latest Posts
Latest Posts
-
4 To Power Of 8
Sep 17, 2025
-
Absolute Value Of 3 4
Sep 17, 2025
-
Half Of 3 3 4 Inches
Sep 17, 2025
-
How High Is 3 Meters
Sep 17, 2025
-
43 Acre To Sq Ft
Sep 17, 2025
Related Post
Thank you for visiting our website which covers about Lcm Of 20 And 10 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.