Lcm Of 20 And 40
saludintensiva
Sep 25, 2025 · 6 min read
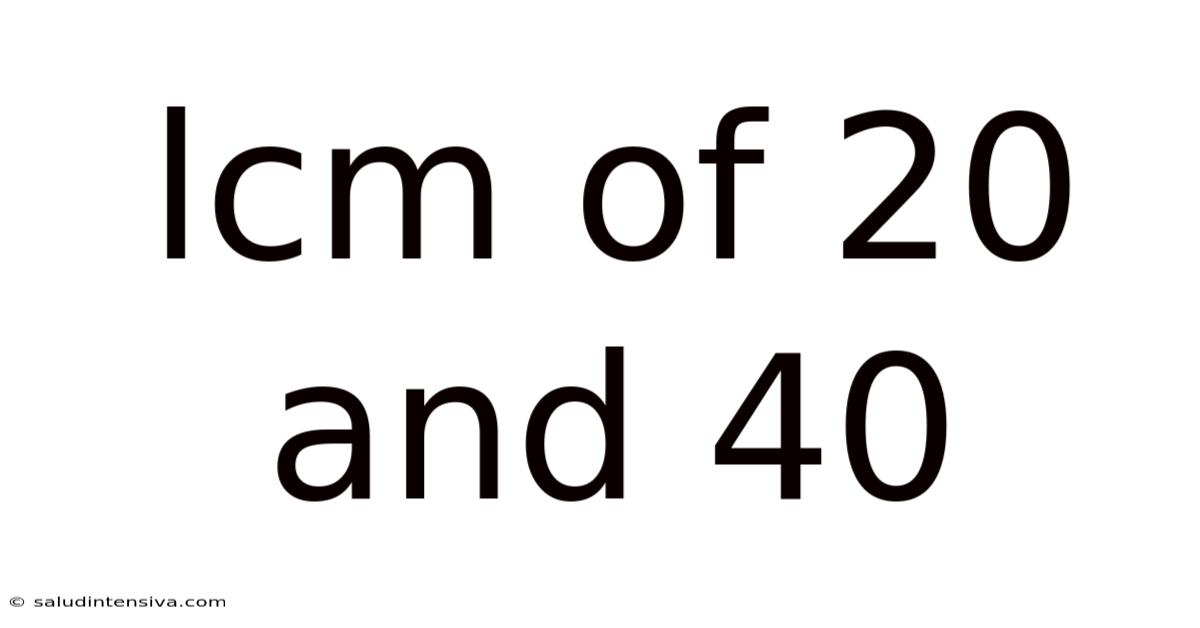
Table of Contents
Understanding the Least Common Multiple (LCM) of 20 and 40: A Comprehensive Guide
Finding the Least Common Multiple (LCM) is a fundamental concept in mathematics, particularly crucial in areas like fractions, ratios, and solving real-world problems involving cycles or repetitions. This article will provide a thorough understanding of how to calculate the LCM of 20 and 40, exploring various methods and delving into the underlying mathematical principles. We'll also examine why understanding LCM is important and explore its applications beyond simple calculations.
What is the Least Common Multiple (LCM)?
The Least Common Multiple (LCM) of two or more numbers is the smallest positive integer that is a multiple of all the numbers. In simpler terms, it's the smallest number that all the given numbers can divide into without leaving a remainder. For example, the LCM of 2 and 3 is 6 because 6 is the smallest number divisible by both 2 and 3.
Methods for Finding the LCM of 20 and 40
Several methods can be used to determine the LCM of 20 and 40. Let's explore the most common ones:
1. Listing Multiples Method
This is the most straightforward approach, especially for smaller numbers. We list the multiples of each number until we find the smallest multiple common to both.
- Multiples of 20: 20, 40, 60, 80, 100, 120...
- Multiples of 40: 40, 80, 120, 160...
The smallest number appearing in both lists is 40. Therefore, the LCM of 20 and 40 is 40.
2. Prime Factorization Method
This method is more efficient for larger numbers and provides a deeper understanding of the concept. We break down each number into its prime factors.
- Prime factorization of 20: 2 x 2 x 5 = 2² x 5
- Prime factorization of 40: 2 x 2 x 2 x 5 = 2³ x 5
To find the LCM, we take the highest power of each prime factor present in the factorizations:
- Highest power of 2: 2³ = 8
- Highest power of 5: 5¹ = 5
Multiply these highest powers together: 2³ x 5 = 40. Therefore, the LCM of 20 and 40 is 40.
3. Greatest Common Divisor (GCD) Method
The LCM and GCD (Greatest Common Divisor) of two numbers are related through a simple formula:
LCM(a, b) x GCD(a, b) = a x b
First, we find the GCD of 20 and 40. Using the Euclidean algorithm or prime factorization, we find that the GCD(20, 40) = 20.
Now, we can use the formula:
LCM(20, 40) x 20 = 20 x 40
LCM(20, 40) = (20 x 40) / 20 = 40
Therefore, the LCM of 20 and 40 is 40.
Understanding the Relationship Between LCM and GCD
The relationship between the LCM and GCD is fundamental to number theory. The formula LCM(a, b) * GCD(a, b) = a * b highlights this interconnectedness. Understanding this relationship allows for efficient calculation of either the LCM or GCD if the other is known. This is particularly useful when dealing with larger numbers where direct prime factorization might be computationally intensive.
Applications of LCM in Real-World Scenarios
The concept of LCM extends beyond abstract mathematical problems; it finds practical application in various real-world scenarios:
-
Scheduling: Imagine two buses depart from a station at different intervals. One bus departs every 20 minutes, and the other every 40 minutes. To find when both buses will depart simultaneously again, we calculate the LCM(20, 40) = 40. Both buses will depart together every 40 minutes.
-
Calendars and Cycles: Determining when specific events will coincide (like the alignment of planets or recurring festivals) often involves calculating the LCM of their respective cycles.
-
Fraction Operations: Finding the least common denominator (LCD) when adding or subtracting fractions requires calculating the LCM of the denominators. For instance, adding 1/20 and 1/40 requires finding the LCD, which is the LCM of 20 and 40 (40).
-
Gear Ratios and Mechanical Systems: In engineering and mechanics, gear ratios and the synchronization of rotating components often rely on the concept of LCM to ensure smooth and efficient operation.
-
Construction and Measurement: In construction and other fields involving measurements, LCM is crucial when dealing with materials of different lengths or dimensions. Finding the smallest common length for cutting materials efficiently often involves using LCM.
Mathematical Properties of LCM
-
Commutative Property: The order in which you calculate the LCM doesn't matter. LCM(a, b) = LCM(b, a).
-
Associative Property: When calculating the LCM of more than two numbers, the order of operation doesn't affect the result. LCM(a, LCM(b, c)) = LCM(LCM(a, b), c).
-
Identity Property: The LCM of any number and 1 is the number itself. LCM(a, 1) = a.
-
LCM of a Number and its Multiple: The LCM of a number and any of its multiples is the multiple. LCM(a, na) = na, where n is an integer.
Frequently Asked Questions (FAQ)
-
Q: What if the numbers are very large? Is there a more efficient method than prime factorization?
- A: For very large numbers, advanced algorithms like the Euclidean algorithm combined with the LCM/GCD relationship are more efficient than direct prime factorization. These algorithms are often implemented in computer programs designed for number-theoretic calculations.
-
Q: Can the LCM of two numbers be smaller than one of the numbers?
- A: No. The LCM will always be greater than or equal to the larger of the two numbers.
-
Q: What is the LCM of more than two numbers?
- A: You can extend the methods discussed earlier to find the LCM of more than two numbers. For example, using prime factorization, you would find the highest power of each prime factor present in the factorization of all the numbers involved.
-
Q: What if the numbers have no common factors?
- A: If the two numbers are relatively prime (they share no common factors other than 1), their LCM is simply the product of the two numbers. For example, LCM(3, 5) = 15.
Conclusion
Finding the LCM of 20 and 40, which is 40, is a simple yet illustrative example of a fundamental mathematical concept. Understanding LCM extends beyond basic calculations. It's a crucial tool applicable to various fields, from scheduling and calendar calculations to engineering and fraction arithmetic. Mastering different methods for calculating the LCM, like prime factorization and the GCD method, equips you with powerful problem-solving skills. By understanding the underlying principles and relationships between LCM and GCD, you can tackle more complex mathematical challenges and appreciate the practical applications of this essential concept in a wide range of situations. The ability to swiftly and accurately calculate the LCM is a valuable asset for anyone seeking a deeper understanding of mathematics and its real-world applications.
Latest Posts
Latest Posts
-
30 Days From Yesterdays Date
Sep 25, 2025
-
Square Inches To Yards Fabric
Sep 25, 2025
-
Rewrite Polynomial In Standard Form
Sep 25, 2025
-
Three Digit Addition With Regrouping
Sep 25, 2025
-
How To Get A 5 0
Sep 25, 2025
Related Post
Thank you for visiting our website which covers about Lcm Of 20 And 40 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.