Lcm Of 27 And 12
saludintensiva
Sep 20, 2025 · 6 min read
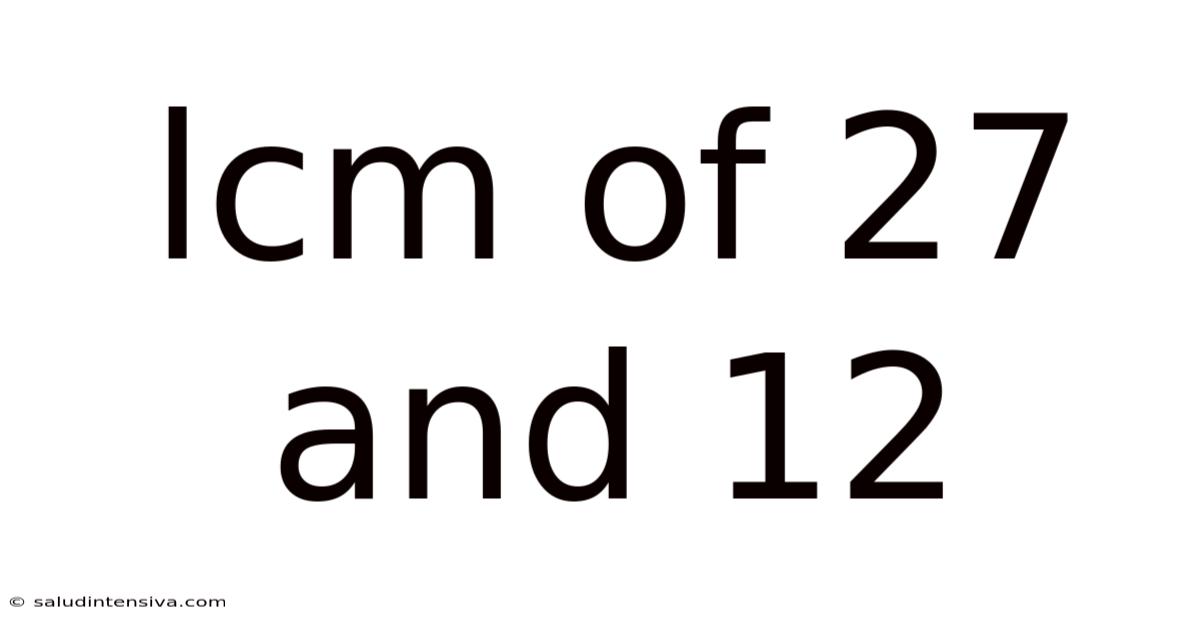
Table of Contents
Finding the LCM of 27 and 12: A Comprehensive Guide
Finding the least common multiple (LCM) of two numbers is a fundamental concept in mathematics, with applications ranging from simple fraction addition to complex scheduling problems. This article will delve into the process of finding the LCM of 27 and 12, exploring various methods, underlying principles, and practical examples. We’ll go beyond a simple answer and equip you with a thorough understanding of LCM, ensuring you can tackle similar problems with confidence. Understanding LCM is crucial for anyone studying arithmetic, algebra, and even more advanced mathematical concepts.
Understanding Least Common Multiple (LCM)
Before we dive into calculating the LCM of 27 and 12, let's clarify what LCM actually means. The least common multiple of two or more integers is the smallest positive integer that is divisible by all the given integers. Think of it as the smallest number that contains all the given numbers as factors. For instance, if we consider the numbers 2 and 3, their multiples are:
- Multiples of 2: 2, 4, 6, 8, 10, 12, 14, 16, 18...
- Multiples of 3: 3, 6, 9, 12, 15, 18...
The common multiples of 2 and 3 are 6, 12, 18, and so on. The smallest of these common multiples is 6, therefore, the LCM of 2 and 3 is 6.
Method 1: Listing Multiples
This is the most straightforward method, especially for smaller numbers. We list the multiples of each number until we find the smallest common multiple.
- Multiples of 27: 27, 54, 81, 108, 135, 162, 189, 216, 243, 270...
- Multiples of 12: 12, 24, 36, 48, 60, 72, 84, 96, 108, 120, 132, 144, 156, 168, 180, 192, 204, 216, 228, 240, 252, 264, 276...
By comparing the lists, we can see that the smallest common multiple of 27 and 12 is 108. Therefore, the LCM(27, 12) = 108. While this method works well for smaller numbers, it becomes less efficient as the numbers get larger.
Method 2: Prime Factorization
This method is more efficient for larger numbers and provides a deeper understanding of the concept. It involves breaking down each number into its prime factors. A prime number is a whole number greater than 1 that has only two divisors: 1 and itself (e.g., 2, 3, 5, 7, 11).
- Prime Factorization of 27: 27 = 3 x 3 x 3 = 3³
- Prime Factorization of 12: 12 = 2 x 2 x 3 = 2² x 3
To find the LCM using prime factorization, we take the highest power of each prime factor present in the factorizations:
- The highest power of 2 is 2² = 4
- The highest power of 3 is 3³ = 27
Now, multiply these highest powers together: 2² x 3³ = 4 x 27 = 108
Therefore, the LCM(27, 12) = 108. This method is generally preferred for its efficiency and conceptual clarity, especially when dealing with larger numbers or multiple numbers.
Method 3: Greatest Common Divisor (GCD) Method
This method utilizes the relationship between the LCM and the greatest common divisor (GCD) of two numbers. The GCD is the largest number that divides both numbers without leaving a remainder. There's a useful formula connecting LCM and GCD:
LCM(a, b) x GCD(a, b) = a x b
Where 'a' and 'b' are the two numbers.
- Finding the GCD of 27 and 12: We can use the Euclidean algorithm to find the GCD.
- 27 = 2 x 12 + 3
- 12 = 4 x 3 + 0
The last non-zero remainder is the GCD, which is 3. Therefore, GCD(27, 12) = 3.
- Applying the formula:
LCM(27, 12) x GCD(27, 12) = 27 x 12 LCM(27, 12) x 3 = 324 LCM(27, 12) = 324 / 3 = 108
Therefore, the LCM(27, 12) = 108. This method elegantly connects the concepts of LCM and GCD, offering another efficient approach.
Illustrative Examples: Real-World Applications
The concept of LCM finds practical applications in various scenarios:
-
Scheduling: Imagine two buses leave a terminal at the same time. One bus departs every 27 minutes, and the other every 12 minutes. When will they both depart simultaneously again? The answer is the LCM(27, 12) = 108 minutes, or 1 hour and 48 minutes.
-
Fraction Addition: To add fractions with different denominators, we need a common denominator, which is usually the LCM of the denominators. For instance, adding 1/27 and 1/12 requires finding the LCM of 27 and 12 (which is 108). Then we convert the fractions:
1/27 = 4/108 1/12 = 9/108
Adding them gives 13/108.
-
Paving Tiles: Suppose you're paving a rectangular area using two types of square tiles. One tile has a side length of 27 cm, and the other has a side length of 12 cm. To avoid cutting tiles, you need to find the smallest square area where both tile types can fit perfectly. This is equivalent to finding the LCM(27, 12) = 108 cm. The smallest square area will have sides of 108 cm.
Frequently Asked Questions (FAQ)
-
What is the difference between LCM and GCD? The LCM is the smallest common multiple, while the GCD is the greatest common divisor. They are inversely related; as the GCD increases, the LCM decreases, and vice versa.
-
Can the LCM of two numbers be smaller than both numbers? No. The LCM of two numbers is always greater than or equal to the larger of the two numbers.
-
How do I find the LCM of more than two numbers? You can extend the prime factorization method or the GCD method to handle more than two numbers. For prime factorization, you consider all prime factors and their highest powers across all numbers. For the GCD method, you can find the GCD of pairs of numbers iteratively.
-
Are there any shortcuts for finding the LCM? If the two numbers are coprime (their GCD is 1), then their LCM is simply their product. Also, understanding prime factorization significantly speeds up the process.
Conclusion
Finding the least common multiple is a fundamental mathematical skill with widespread applications. We've explored three effective methods: listing multiples, prime factorization, and the GCD method. Prime factorization is generally the most efficient and conceptually insightful method, especially for larger numbers. Understanding these methods will not only help you solve LCM problems but will also provide a strong foundation for more advanced mathematical concepts. Remember to practice regularly to improve your proficiency and build confidence in tackling these types of problems. The more you practice, the more intuitive this process will become. The applications of LCM extend far beyond simple arithmetic exercises, making it a vital concept to master in your mathematical journey.
Latest Posts
Latest Posts
-
175 Cm To Feet Conversion
Sep 20, 2025
-
Where Is The Thousandths Place
Sep 20, 2025
-
Value Of 50 Cent Coins
Sep 20, 2025
-
1 21 As A Percentage
Sep 20, 2025
-
60 Days After March 1
Sep 20, 2025
Related Post
Thank you for visiting our website which covers about Lcm Of 27 And 12 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.