Lcm Of 30 And 42
saludintensiva
Sep 15, 2025 · 6 min read
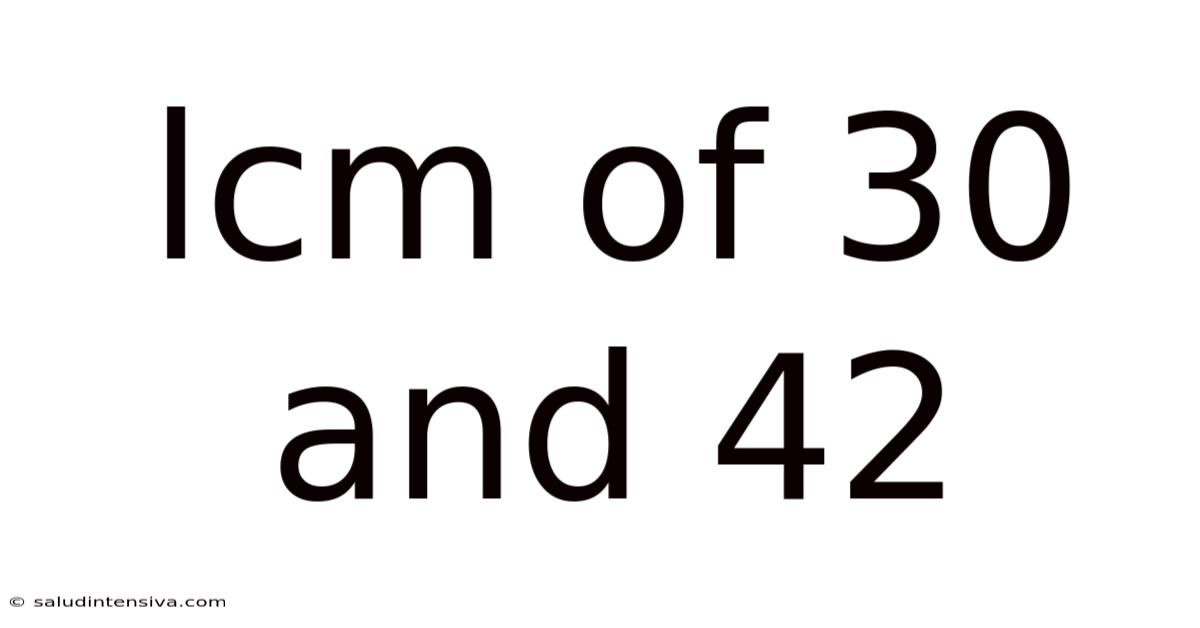
Table of Contents
Finding the Least Common Multiple (LCM) of 30 and 42: A Comprehensive Guide
Finding the least common multiple (LCM) of two numbers might seem like a simple arithmetic task, but understanding the underlying principles unlocks a deeper appreciation of number theory and its applications. This comprehensive guide will explore various methods for calculating the LCM of 30 and 42, delving into the concepts behind these methods and showcasing their practical uses. We'll also address frequently asked questions and provide examples to solidify your understanding. This guide aims to equip you with not just the answer, but a thorough understanding of the process.
Understanding Least Common Multiple (LCM)
The least common multiple (LCM) of two or more integers is the smallest positive integer that is divisible by all the integers. In simpler terms, it's the smallest number that contains all the numbers as factors. Understanding LCM is crucial in various mathematical applications, from solving fraction problems to determining the timing of recurring events.
Consider two numbers, 30 and 42. We are looking for the smallest number that is a multiple of both 30 and 42. Let's explore several methods to find this number.
Method 1: Listing Multiples
This is a straightforward, albeit potentially time-consuming, method, especially for larger numbers. We list the multiples of each number until we find the smallest common multiple.
Multiples of 30: 30, 60, 90, 120, 150, 180, 210, 240, 270, 300, ...
Multiples of 42: 42, 84, 126, 168, 210, 252, 294, 336, ...
By comparing the lists, we can see that the smallest number appearing in both lists is 210. Therefore, the LCM of 30 and 42 is 210. This method is effective for smaller numbers but becomes impractical for larger ones.
Method 2: Prime Factorization
This method is more efficient and systematic, particularly for larger numbers. It involves finding the prime factorization of each number and then constructing the LCM using the highest powers of each prime factor present.
Prime Factorization of 30:
30 = 2 x 3 x 5
Prime Factorization of 42:
42 = 2 x 3 x 7
Now, we identify the unique prime factors present in both factorizations: 2, 3, 5, and 7. To find the LCM, we take the highest power of each prime factor:
- 2: The highest power is 2¹ (from both 30 and 42).
- 3: The highest power is 3¹ (from both 30 and 42).
- 5: The highest power is 5¹ (from 30).
- 7: The highest power is 7¹ (from 42).
Multiplying these highest powers together gives us the LCM:
LCM(30, 42) = 2¹ x 3¹ x 5¹ x 7¹ = 2 x 3 x 5 x 7 = 210
This method is significantly more efficient than listing multiples, particularly when dealing with larger numbers.
Method 3: Using the Greatest Common Divisor (GCD)
The LCM and the greatest common divisor (GCD) of two numbers are related through a simple formula:
LCM(a, b) x GCD(a, b) = a x b
Where 'a' and 'b' are the two numbers. First, we need to find the GCD of 30 and 42. We can use the Euclidean algorithm for this:
- Divide the larger number (42) by the smaller number (30): 42 ÷ 30 = 1 with a remainder of 12.
- Replace the larger number with the smaller number (30) and the smaller number with the remainder (12): 30 ÷ 12 = 2 with a remainder of 6.
- Repeat the process: 12 ÷ 6 = 2 with a remainder of 0.
The last non-zero remainder is the GCD, which is 6.
Now, we can use the formula:
LCM(30, 42) = (30 x 42) / GCD(30, 42) = (30 x 42) / 6 = 1260 / 6 = 210
This method is also efficient and relies on a well-established algorithm for finding the GCD.
Applications of LCM
The LCM finds applications in diverse areas:
- Fraction Addition and Subtraction: Finding a common denominator when adding or subtracting fractions requires finding the LCM of the denominators.
- Cyclic Events: Determining when events with different cycles will occur simultaneously (e.g., two trains departing at different intervals).
- Gear Ratios: Calculating the speed and synchronization of gears in mechanical systems.
- Scheduling and Planning: Determining the optimal time for recurring tasks or events.
- Music Theory: Understanding harmonic relationships and intervals in music.
Why is Understanding LCM Important?
Beyond the immediate application in solving specific mathematical problems, understanding LCM builds foundational mathematical skills. It reinforces concepts of divisibility, prime factorization, and the relationships between numbers. These skills are essential for more advanced mathematical studies. The ability to efficiently find the LCM also translates to problem-solving skills in various fields, promoting critical thinking and logical reasoning.
Frequently Asked Questions (FAQ)
Q1: What if the numbers have no common factors?
If the numbers are relatively prime (meaning their GCD is 1), their LCM is simply the product of the two numbers. For example, LCM(5, 7) = 5 x 7 = 35.
Q2: Can the LCM of two numbers be smaller than both numbers?
No. The LCM will always be greater than or equal to the larger of the two numbers.
Q3: How do I find the LCM of more than two numbers?
You can extend the prime factorization method or the GCD method to accommodate more than two numbers. For example, to find the LCM of 12, 18, and 30, you would find the prime factorization of each number and then select the highest power of each prime factor present across all three factorizations.
Q4: Is there a formula for finding the LCM of three or more numbers?
There isn't a single, concise formula like the one relating LCM and GCD for two numbers, but the process of finding the prime factorization and using the highest powers remains consistent for any number of integers.
Q5: What is the relationship between LCM and GCD?
The LCM and GCD of two integers, a and b, are related by the equation: LCM(a, b) × GCD(a, b) = a × b. This relationship provides a powerful method for calculating the LCM if you already know the GCD.
Conclusion
Finding the least common multiple of 30 and 42, which we have determined to be 210, illustrates several important mathematical concepts. We explored three different methods—listing multiples, prime factorization, and using the GCD—each offering a unique perspective on the problem. The choice of method depends on the context and the magnitude of the numbers involved. Understanding LCM isn't merely about obtaining a numerical answer; it's about mastering fundamental mathematical principles and developing critical thinking skills applicable to various fields. The ability to efficiently and accurately calculate LCM enhances problem-solving abilities and provides a solid foundation for more advanced mathematical concepts. This comprehensive guide aims to not just provide the answer but also build your understanding of the underlying principles and their practical applications. Remember that consistent practice and exploration are key to solidifying your comprehension of LCM and its importance within the broader landscape of mathematics.
Latest Posts
Latest Posts
-
Gcf Of 28 And 35
Sep 15, 2025
-
2 3 As Mixed Number
Sep 15, 2025
-
8 Out Of 11 Percentage
Sep 15, 2025
-
1 89 M In Feet
Sep 15, 2025
-
6 11 As A Decimal
Sep 15, 2025
Related Post
Thank you for visiting our website which covers about Lcm Of 30 And 42 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.