Lcm Of 36 And 16
saludintensiva
Sep 17, 2025 · 6 min read
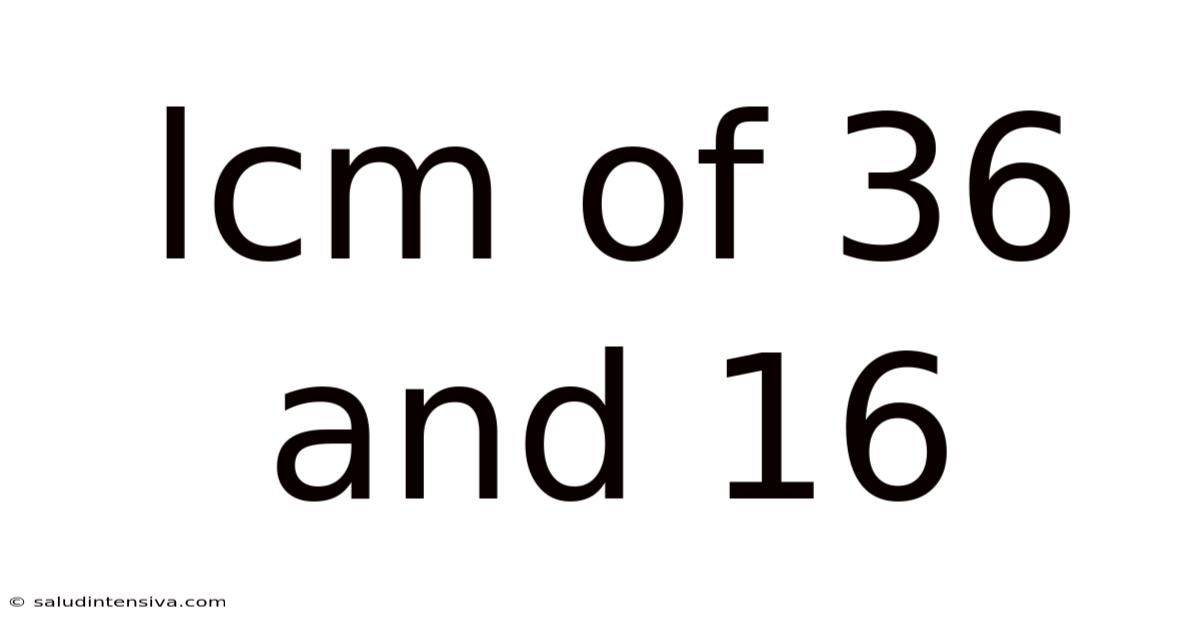
Table of Contents
Finding the Least Common Multiple (LCM) of 36 and 16: A Comprehensive Guide
Finding the least common multiple (LCM) might seem like a simple arithmetic task, but understanding the underlying principles and different methods for calculating it is crucial for a strong foundation in mathematics. This article delves into the concept of LCM, focusing specifically on finding the LCM of 36 and 16. We'll explore multiple approaches, including prime factorization, the listing method, and using the greatest common divisor (GCD), ensuring a comprehensive understanding for students and enthusiasts alike. This guide will cover everything from the basic definitions to advanced techniques, providing a solid grasp of this important mathematical concept.
Understanding Least Common Multiple (LCM)
The least common multiple (LCM) of two or more integers is the smallest positive integer that is a multiple of all the integers. In simpler terms, it's the smallest number that can be divided evenly by all the given numbers without leaving a remainder. Understanding LCM is vital in various mathematical applications, including solving problems involving fractions, finding common denominators, and understanding rhythmic patterns in music.
Method 1: Prime Factorization
This is arguably the most efficient and systematic method for finding the LCM of larger numbers. It involves breaking down each number into its prime factors.
Step 1: Prime Factorization of 36
36 can be broken down as follows:
36 = 2 x 18 = 2 x 2 x 9 = 2 x 2 x 3 x 3 = 2² x 3²
Step 2: Prime Factorization of 16
16 can be broken down as follows:
16 = 2 x 8 = 2 x 2 x 4 = 2 x 2 x 2 x 2 = 2⁴
Step 3: Identifying Common and Uncommon Factors
Now, we compare the prime factorizations of 36 and 16:
36 = 2² x 3² 16 = 2⁴
We see that both numbers share the prime factor 2. However, they have different exponents. We also have the prime factor 3 which is unique to 36.
Step 4: Calculating the LCM
To find the LCM, we take the highest power of each prime factor present in either factorization and multiply them together.
LCM(36, 16) = 2⁴ x 3² = 16 x 9 = 144
Therefore, the least common multiple of 36 and 16 is 144. This means 144 is the smallest number that is divisible by both 36 and 16 without leaving a remainder.
Method 2: Listing Multiples
This method is more intuitive but can be less efficient for larger numbers. It involves listing the multiples of each number until a common multiple is found.
Step 1: Listing Multiples of 36
Multiples of 36: 36, 72, 108, 144, 180, 216, 252, 288, ...
Step 2: Listing Multiples of 16
Multiples of 16: 16, 32, 48, 64, 80, 96, 112, 128, 144, 160, ...
Step 3: Identifying the Least Common Multiple
By comparing the lists, we can see that the smallest number that appears in both lists is 144. Therefore, the LCM(36, 16) = 144.
This method is straightforward for smaller numbers but becomes cumbersome when dealing with larger numbers.
Method 3: Using the Greatest Common Divisor (GCD)
The LCM and GCD (Greatest Common Divisor) of two numbers are closely related. There's a formula that connects them:
LCM(a, b) = (|a x b|) / GCD(a, b)
where |a x b| represents the absolute value of the product of a and b.
Step 1: Finding the GCD of 36 and 16
We can use the Euclidean algorithm to find the GCD.
- Divide 36 by 16: 36 = 16 x 2 + 4
- Divide 16 by the remainder 4: 16 = 4 x 4 + 0
The last non-zero remainder is 4, so GCD(36, 16) = 4.
Step 2: Calculating the LCM using the formula
LCM(36, 16) = (36 x 16) / 4 = 576 / 4 = 144
This method provides an alternative approach, particularly useful when the GCD is readily available or easily calculated.
Illustrative Examples and Applications of LCM
The LCM has numerous applications beyond simple arithmetic exercises. Let's explore some examples:
-
Scheduling: Imagine two buses depart from the same station. One bus departs every 36 minutes, and the other departs every 16 minutes. The LCM(36, 16) = 144 minutes tells us that both buses will depart at the same time again after 144 minutes (2 hours and 24 minutes).
-
Fraction Addition and Subtraction: When adding or subtracting fractions with different denominators, finding the LCM of the denominators helps determine the least common denominator (LCD), simplifying the calculation. For example, to add 1/36 and 1/16, you would find the LCD which is 144, converting the fractions to 4/144 and 9/144 respectively, making addition much easier.
-
Tiling and Pattern Repetition: Consider tiling a floor using two types of tiles. One tile is 36 cm wide, and the other is 16 cm wide. The LCM(36, 16) = 144 cm determines the shortest length of a continuous row where both tile types can perfectly fit without any cutting or gaps.
-
Music and Rhythm: In music, LCM helps determine when rhythmic patterns repeat simultaneously. If one musical phrase repeats every 36 beats and another every 16 beats, they will coincide again after 144 beats.
Frequently Asked Questions (FAQ)
Q: Is there only one LCM for two numbers?
A: Yes, there is only one least common multiple for any pair of numbers. While there are many common multiples, only one is the smallest.
Q: What if one of the numbers is 0?
A: The LCM of any number and 0 is undefined. This is because 0 is a multiple of every number, leading to infinitely many common multiples.
Q: Can I use a calculator to find the LCM?
A: Many scientific calculators have built-in functions to calculate the LCM. However, understanding the underlying methods is crucial for problem-solving and deeper mathematical understanding.
Q: Which method is the best?
A: The prime factorization method is generally the most efficient and reliable, especially for larger numbers. The listing method is suitable for smaller numbers and provides a visual understanding. The GCD method is helpful when the GCD is already known.
Conclusion
Finding the LCM of 36 and 16, which we've determined to be 144, is more than just a simple arithmetic exercise. It showcases a fundamental concept in mathematics with broad applications. Understanding the different methods—prime factorization, listing multiples, and using the GCD—provides a versatile toolkit for approaching various LCM problems. The ability to efficiently determine the LCM is a valuable skill, essential for success in mathematics and related fields. By grasping the concepts explored in this article, you'll build a stronger mathematical foundation and appreciate the wide-ranging applicability of the least common multiple. Remember to practice these methods with different numbers to solidify your understanding. The more you practice, the more proficient and confident you'll become in solving LCM problems.
Latest Posts
Latest Posts
-
2 3 8 In Decimal Form
Sep 17, 2025
-
Greatest Common Factor Of 38
Sep 17, 2025
-
2 To The 4 Power
Sep 17, 2025
-
27 35 As A Percentage
Sep 17, 2025
-
Convert 300 Kelvin Into Celsius
Sep 17, 2025
Related Post
Thank you for visiting our website which covers about Lcm Of 36 And 16 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.