Lcm Of 4 8 12
saludintensiva
Sep 10, 2025 · 6 min read
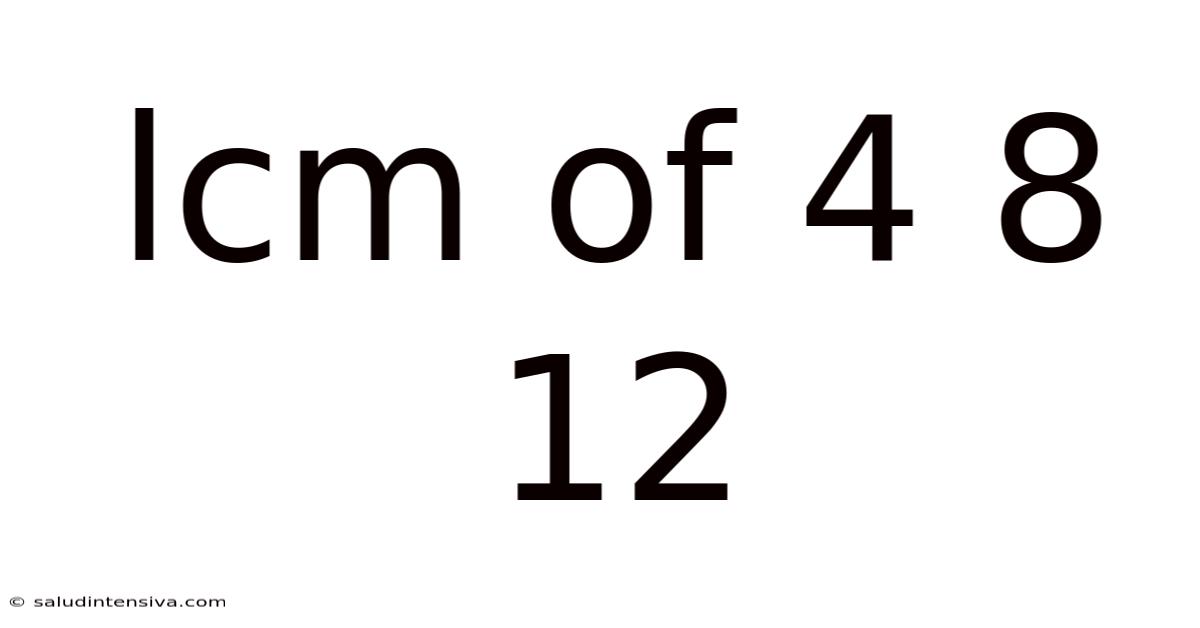
Table of Contents
Finding the Least Common Multiple (LCM) of 4, 8, and 12: A Comprehensive Guide
Finding the Least Common Multiple (LCM) might seem like a simple arithmetic task, but understanding the underlying concepts and different methods for calculating it is crucial for a strong foundation in mathematics. This comprehensive guide will walk you through various ways to determine the LCM of 4, 8, and 12, explaining the process in detail and exploring the broader significance of LCMs in various mathematical applications. We'll cover everything from the basic method of listing multiples to the more efficient prime factorization method, ensuring you gain a complete understanding of this fundamental concept.
Understanding Least Common Multiples (LCM)
Before we dive into calculating the LCM of 4, 8, and 12, let's establish a clear understanding of what an LCM actually is. The Least Common Multiple (LCM) of two or more numbers is the smallest positive integer that is a multiple of all the numbers. In simpler terms, it's the smallest number that all the given numbers can divide into evenly without leaving a remainder. Understanding LCMs is essential in various areas, including:
- Fraction Arithmetic: Finding a common denominator when adding or subtracting fractions.
- Scheduling Problems: Determining when events will occur simultaneously (e.g., buses arriving at a stop).
- Measurement Conversions: Finding the smallest common unit for measurement.
Method 1: Listing Multiples
The most straightforward method for finding the LCM of smaller numbers is to list the multiples of each number until you find the smallest common multiple. Let's apply this to 4, 8, and 12:
- Multiples of 4: 4, 8, 12, 16, 20, 24, 28, 32, 36, 40...
- Multiples of 8: 8, 16, 24, 32, 40, 48...
- Multiples of 12: 12, 24, 36, 48...
By examining the lists, we can see that the smallest number that appears in all three lists is 24. Therefore, the LCM of 4, 8, and 12 is 24.
This method is effective for smaller numbers, but it becomes less practical as the numbers get larger. Imagine trying to find the LCM of 144, 288, and 360 using this approach – it would be incredibly time-consuming! This highlights the need for more efficient methods.
Method 2: Prime Factorization
The prime factorization method is a more efficient and systematic approach to finding the LCM, especially for larger numbers. This method involves breaking down each number into its prime factors. Prime factors are numbers that are only divisible by 1 and themselves (e.g., 2, 3, 5, 7, 11...).
Let's find the prime factorization of 4, 8, and 12:
- 4 = 2 x 2 = 2²
- 8 = 2 x 2 x 2 = 2³
- 12 = 2 x 2 x 3 = 2² x 3
Now, to find the LCM, we take the highest power of each prime factor that appears in any of the factorizations and multiply them together:
- The highest power of 2 is 2³ = 8
- The highest power of 3 is 3¹ = 3
Therefore, the LCM of 4, 8, and 12 is 8 x 3 = 24.
Method 3: Greatest Common Divisor (GCD) Method
The LCM and the Greatest Common Divisor (GCD) are closely related. The GCD is the largest number that divides all the given numbers without leaving a remainder. There's a useful relationship between the LCM and GCD:
LCM(a, b) x GCD(a, b) = a x b
This formula applies to two numbers (a and b). To extend it to three or more numbers, we can use it iteratively. Let's find the LCM of 4, 8, and 12 using this method:
- Find the GCD of 4 and 8: The GCD of 4 and 8 is 4.
- Find the LCM of 4 and 8: Using the formula, LCM(4, 8) x GCD(4, 8) = 4 x 8. Therefore, LCM(4, 8) = (4 x 8) / 4 = 8.
- Find the GCD of 8 and 12: The GCD of 8 and 12 is 4.
- Find the LCM of 8 and 12: Using the formula, LCM(8, 12) x GCD(8, 12) = 8 x 12. Therefore, LCM(8, 12) = (8 x 12) / 4 = 24.
Thus, the LCM of 4, 8, and 12 is 24. This method is particularly useful when dealing with larger numbers where prime factorization might become more complex.
Illustrative Examples: Real-World Applications of LCM
Let's explore some real-world scenarios where understanding LCM is crucial:
-
Scheduling Bus Routes: Imagine two bus routes, one arriving every 4 minutes and the other every 8 minutes. To find out when both buses arrive at the same stop simultaneously, you need to calculate the LCM of 4 and 8, which is 8. Both buses will arrive together every 8 minutes.
-
Baking: A recipe calls for 1/4 cup of sugar and 1/12 cup of baking powder. To combine these ingredients accurately, you need a common denominator. Finding the LCM of 4 and 12 (which is 12) allows you to convert the fractions to have a common denominator of 12, making the addition simpler.
-
Project Planning: Consider a project with three tasks: Task A takes 12 hours, Task B takes 8 hours, and Task C takes 4 hours. To determine the least amount of time required to complete all three tasks efficiently, you would need to find the LCM of 12, 8, and 4. This will indicate the shortest time frame before all tasks could be finished simultaneously given optimal scheduling.
Frequently Asked Questions (FAQ)
-
Q: What if the numbers have no common factors?
A: If the numbers are relatively prime (meaning they share no common factors other than 1), then their LCM is simply the product of the numbers.
-
Q: Can I use a calculator to find the LCM?
A: Many scientific calculators have built-in functions to calculate the LCM of numbers. However, understanding the methods behind the calculation is essential for a deeper mathematical understanding.
-
Q: Is there a difference between LCM and GCD?
A: Yes, the LCM is the smallest multiple common to all given numbers, while the GCD is the greatest divisor common to all given numbers. They are inversely related, as shown by the formula connecting them.
Conclusion
Finding the Least Common Multiple (LCM) is a fundamental skill in mathematics with wide-ranging applications. This guide has presented various methods for calculating the LCM of 4, 8, and 12, illustrating the practicality and efficiency of different approaches. Whether you use the method of listing multiples, prime factorization, or the GCD method, the ultimate result remains the same: the LCM of 4, 8, and 12 is 24. Understanding these methods not only helps solve specific mathematical problems but also fosters a deeper understanding of number theory and its real-world applications. The ability to confidently tackle LCM calculations lays a strong groundwork for more advanced mathematical concepts and problem-solving skills. Remember that the key to mastering LCM is understanding the underlying principles and selecting the most appropriate method based on the numbers involved.
Latest Posts
Latest Posts
-
4 To The 0 Power
Sep 10, 2025
-
8am 8pm Is How Many Hours
Sep 10, 2025
-
What Is Equivalent To 9 4
Sep 10, 2025
-
What Is 12 3 Simplified
Sep 10, 2025
-
What Are Multiples Of 15
Sep 10, 2025
Related Post
Thank you for visiting our website which covers about Lcm Of 4 8 12 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.