Lcm Of 42 And 30
saludintensiva
Sep 15, 2025 · 5 min read
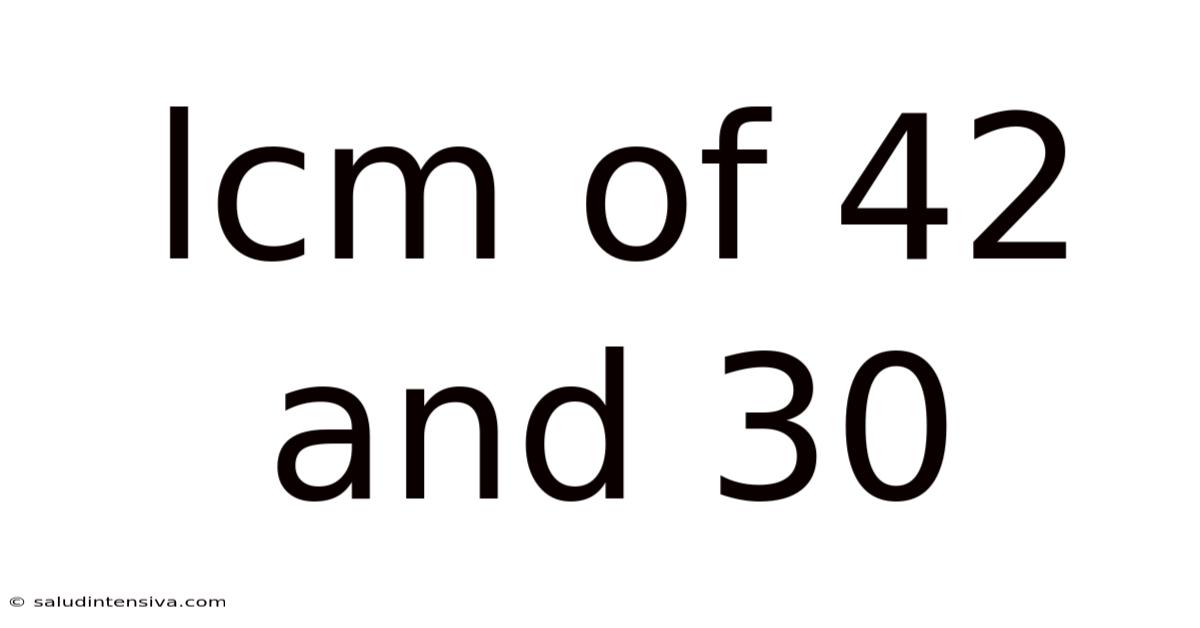
Table of Contents
Finding the LCM of 42 and 30: A Comprehensive Guide
Finding the least common multiple (LCM) of two numbers, like 42 and 30, might seem like a simple arithmetic task. However, understanding the underlying principles and different methods for calculating the LCM provides a valuable foundation in number theory and is essential for various mathematical applications. This article delves into the concept of LCM, explores multiple approaches to calculating the LCM of 42 and 30, and expands on the broader significance of this concept in mathematics.
Understanding Least Common Multiple (LCM)
The least common multiple (LCM) of two or more integers is the smallest positive integer that is a multiple of each of the integers. In simpler terms, it's the smallest number that both numbers can divide into evenly without leaving a remainder. Understanding LCM is crucial for solving problems related to fractions, cycles, and rhythmic patterns. For example, if two gears with 42 and 30 teeth are rotating, finding their LCM helps determine when they will both be at their starting position simultaneously.
Method 1: Listing Multiples
The most straightforward method to find the LCM is by listing the multiples of each number until a common multiple is found. Let's apply this to 42 and 30:
- Multiples of 42: 42, 84, 126, 168, 210, 252, 294, 336, 378, 420, ...
- Multiples of 30: 30, 60, 90, 120, 150, 180, 210, 240, 270, 300, ...
By comparing the lists, we see that the smallest common multiple is 210. Therefore, the LCM of 42 and 30 is 210. While this method works well for smaller numbers, it becomes less efficient as the numbers increase in size.
Method 2: Prime Factorization
This method is more efficient, especially for larger numbers. It involves finding the prime factorization of each number and then constructing the LCM using the highest powers of all prime factors present.
Step 1: Prime Factorization:
Let's find the prime factorization of 42 and 30:
- 42 = 2 × 3 × 7
- 30 = 2 × 3 × 5
Step 2: Constructing the LCM:
The prime factors involved are 2, 3, 5, and 7. To find the LCM, we take the highest power of each prime factor present in either factorization:
- Highest power of 2: 2¹ = 2
- Highest power of 3: 3¹ = 3
- Highest power of 5: 5¹ = 5
- Highest power of 7: 7¹ = 7
Now, multiply these highest powers together:
LCM(42, 30) = 2 × 3 × 5 × 7 = 210
Therefore, the LCM of 42 and 30 is 210, confirming the result from the previous method. This method is generally preferred for its efficiency and scalability.
Method 3: Using the Greatest Common Divisor (GCD)
The LCM and the greatest common divisor (GCD) of two numbers are closely related. The product of the LCM and GCD of two numbers is equal to the product of the two numbers. This relationship is expressed as:
LCM(a, b) × GCD(a, b) = a × b
where 'a' and 'b' are the two numbers.
Step 1: Finding the GCD:
We can find the GCD of 42 and 30 using the Euclidean algorithm:
- Divide the larger number (42) by the smaller number (30): 42 ÷ 30 = 1 with a remainder of 12.
- Replace the larger number with the smaller number (30) and the smaller number with the remainder (12): 30 ÷ 12 = 2 with a remainder of 6.
- Repeat the process: 12 ÷ 6 = 2 with a remainder of 0.
- The GCD is the last non-zero remainder, which is 6.
Step 2: Calculating the LCM:
Now, we can use the relationship between LCM and GCD:
LCM(42, 30) = (42 × 30) / GCD(42, 30) = (42 × 30) / 6 = 210
This method provides another efficient way to find the LCM, particularly when dealing with larger numbers where prime factorization might be more laborious.
Applications of LCM
The concept of LCM extends far beyond simple arithmetic exercises. Here are some real-world applications:
-
Scheduling: Determining when events will coincide. For example, if one event occurs every 42 days and another every 30 days, the LCM (210 days) indicates when both events will occur on the same day.
-
Fraction Addition and Subtraction: Finding a common denominator when adding or subtracting fractions. To add 1/42 and 1/30, you would find the LCM of 42 and 30 (which is 210) and convert the fractions to have this common denominator.
-
Gear Ratios: In mechanical engineering, LCM is used to calculate the synchronization of gears with different numbers of teeth.
-
Cyclic Processes: Determining when cyclical processes will align. This is applicable in various fields, from music (finding the least common multiple of note durations) to astronomy (calculating planetary alignments).
-
Modular Arithmetic: In computer science and cryptography, LCM plays a vital role in modular arithmetic operations, especially in areas dealing with cyclical patterns and data encryption.
Frequently Asked Questions (FAQ)
-
Q: What if I need to find the LCM of more than two numbers?
A: You can extend the prime factorization method or the GCD method to include multiple numbers. For prime factorization, you consider all prime factors from all numbers and take the highest power of each. For the GCD method, you can iteratively find the GCD of pairs of numbers and then use the result to find the LCM.
-
Q: Is there a formula for LCM?
A: There isn't a single, universally applicable formula for LCM, but the relationship between LCM and GCD provides a powerful tool for calculation: LCM(a, b) = (a × b) / GCD(a, b). Prime factorization provides a procedural method, and listing multiples is a direct but less efficient approach.
-
Q: What if the numbers are very large?
A: For extremely large numbers, specialized algorithms and computational tools are employed to efficiently find the LCM. These algorithms often optimize the prime factorization process or leverage advanced mathematical properties.
Conclusion
Finding the LCM of 42 and 30, whether through listing multiples, prime factorization, or utilizing the GCD, highlights the fundamental importance of this concept in mathematics. While seemingly simple, the LCM has profound implications across various disciplines and underscores the interconnectedness of mathematical principles. Understanding different approaches to calculating the LCM enhances problem-solving skills and provides a solid foundation for tackling more complex mathematical challenges. The methods explained here provide a versatile toolkit for handling LCM calculations, making it an essential tool in any mathematician's arsenal. Remember, choosing the most efficient method depends on the specific numbers involved and the context of the problem.
Latest Posts
Latest Posts
-
Gcf Of 36 And 20
Sep 16, 2025
-
Rounding To Nearest Ten Thousand
Sep 16, 2025
-
12 100 As A Decimal
Sep 16, 2025
-
1 4 Is Equal To
Sep 16, 2025
-
How To Figure Square Inches
Sep 16, 2025
Related Post
Thank you for visiting our website which covers about Lcm Of 42 And 30 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.