Lcm Of 45 And 75
saludintensiva
Sep 19, 2025 · 6 min read
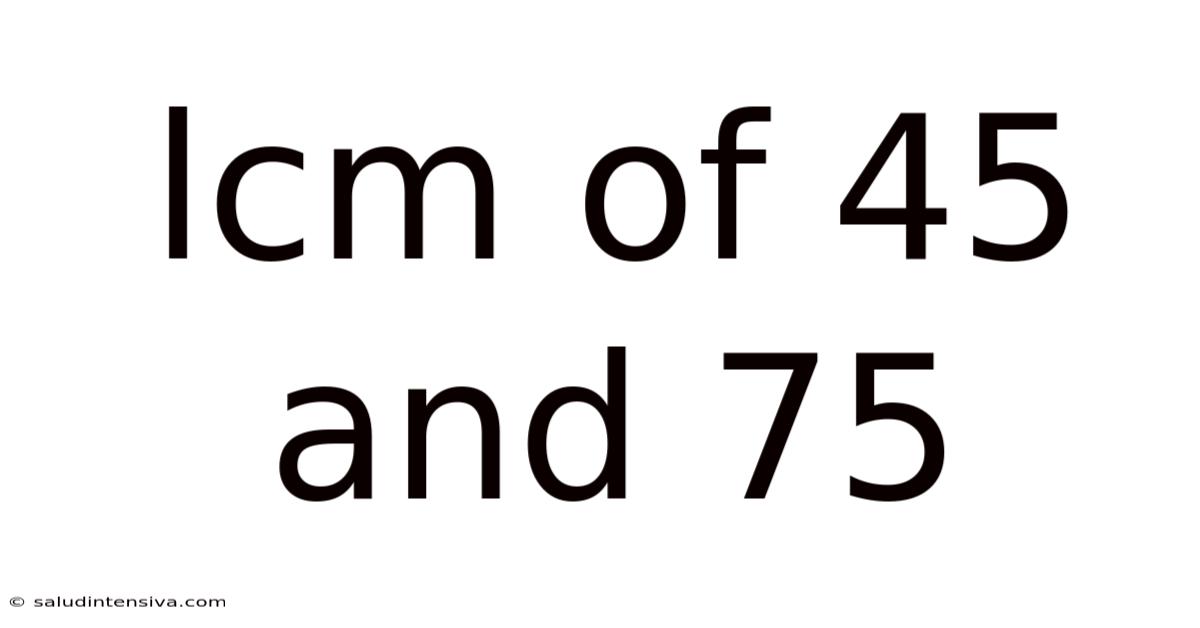
Table of Contents
Finding the LCM of 45 and 75: A Comprehensive Guide
Finding the least common multiple (LCM) of two numbers is a fundamental concept in mathematics, crucial for various applications ranging from simple fraction operations to complex scheduling problems. This comprehensive guide will walk you through several methods to determine the LCM of 45 and 75, providing a deep understanding of the underlying principles and practical applications. We'll explore different approaches, from listing multiples to using prime factorization, ensuring you grasp this concept thoroughly. Understanding LCM is key to mastering more advanced mathematical topics.
Introduction: What is the Least Common Multiple (LCM)?
The least common multiple (LCM) of two or more integers is the smallest positive integer that is divisible by all the numbers. In simpler terms, it's the smallest number that contains all the numbers as factors. For instance, the LCM of 2 and 3 is 6 because 6 is the smallest number divisible by both 2 and 3. Finding the LCM is a valuable tool in various mathematical operations, particularly when dealing with fractions, simplifying expressions, and solving real-world problems involving cycles or repetitions.
Method 1: Listing Multiples
This is the most straightforward method, especially for smaller numbers like 45 and 75. We simply list the multiples of each number until we find the smallest multiple common to both.
- Multiples of 45: 45, 90, 135, 180, 225, 270, 315, 360...
- Multiples of 75: 75, 150, 225, 300, 375...
By comparing the lists, we can see that the smallest multiple appearing in both lists is 225. Therefore, the LCM of 45 and 75 is 225.
This method is easy to understand but becomes less efficient when dealing with larger numbers. Let's explore more sophisticated methods.
Method 2: Prime Factorization
Prime factorization is a powerful technique for finding the LCM of larger numbers. It involves expressing each number as a product of its prime factors. A prime number is a whole number greater than 1 that has only two divisors: 1 and itself (e.g., 2, 3, 5, 7, 11...).
Let's find the prime factorization of 45 and 75:
- 45 = 3 x 3 x 5 = 3² x 5
- 75 = 3 x 5 x 5 = 3 x 5²
Now, to find the LCM, we take the highest power of each prime factor present in the factorizations:
- The highest power of 3 is 3² = 9.
- The highest power of 5 is 5² = 25.
Multiply these highest powers together: 9 x 25 = 225. Therefore, the LCM of 45 and 75 is 225, confirming our result from the previous method.
This method is more efficient than listing multiples, especially for larger numbers, as it directly identifies the essential prime factors.
Method 3: Using the Greatest Common Divisor (GCD)
The LCM and the greatest common divisor (GCD) of two numbers are closely related. The GCD is the largest number that divides both numbers without leaving a remainder. We can use the following formula to find the LCM:
LCM(a, b) = (a x b) / GCD(a, b)
First, let's find the GCD of 45 and 75. We can use the Euclidean algorithm for this:
- Divide the larger number (75) by the smaller number (45): 75 ÷ 45 = 1 with a remainder of 30.
- Replace the larger number with the smaller number (45) and the smaller number with the remainder (30): 45 ÷ 30 = 1 with a remainder of 15.
- Repeat: 30 ÷ 15 = 2 with a remainder of 0.
The last non-zero remainder is the GCD, which is 15.
Now, we can use the formula:
LCM(45, 75) = (45 x 75) / 15 = 3375 / 15 = 225
Again, we arrive at the same result: the LCM of 45 and 75 is 225. This method is particularly useful when dealing with larger numbers, as finding the GCD is often easier than directly finding the LCM.
Understanding the Relationship Between LCM and GCD
The relationship between LCM and GCD is mathematically elegant and fundamental. The product of the LCM and GCD of two numbers always equals the product of the two numbers themselves:
LCM(a, b) x GCD(a, b) = a x b
This relationship provides a powerful alternative method for calculating the LCM, especially when the GCD is readily available or easier to compute.
Real-World Applications of LCM
The concept of LCM has practical applications in various real-world scenarios:
-
Scheduling: Imagine two buses depart from the same stop, one every 45 minutes and the other every 75 minutes. The LCM (225 minutes) represents the time when both buses will depart simultaneously again.
-
Fraction Operations: When adding or subtracting fractions with different denominators, finding the LCM of the denominators is crucial for finding a common denominator, simplifying the calculation.
-
Cyclic Processes: In various engineering and scientific applications involving periodic or cyclical processes, the LCM helps determine when events will coincide or repeat.
-
Project Management: In project scheduling, determining the LCM of different task durations can help optimize the overall project timeline.
Frequently Asked Questions (FAQ)
-
Q: What if the numbers have no common factors other than 1?
- A: If the GCD of two numbers is 1, they are called relatively prime or coprime. In this case, their LCM is simply the product of the two numbers.
-
Q: Can I find the LCM of more than two numbers?
- A: Yes, you can extend the methods described above to find the LCM of multiple numbers. For prime factorization, you would consider all prime factors from all numbers and take the highest power of each. For the GCD-based method, you'd need to find the GCD of all numbers iteratively.
-
Q: Is there a single "best" method for finding the LCM?
- A: The best method depends on the numbers involved and your familiarity with the techniques. For small numbers, listing multiples is straightforward. For larger numbers, prime factorization or the GCD method is generally more efficient.
-
Q: What is the significance of LCM in advanced mathematics?
- A: LCM plays a crucial role in abstract algebra, number theory, and other advanced mathematical fields. It’s a building block for understanding modular arithmetic, group theory, and other complex concepts.
Conclusion: Mastering the LCM
Finding the least common multiple is a fundamental skill in mathematics with far-reaching applications. This comprehensive guide has explored three distinct methods for calculating the LCM, focusing on the practical calculation for 45 and 75 while emphasizing the broader mathematical concepts. By mastering these techniques and understanding the underlying principles, you'll be equipped to tackle more complex mathematical problems and appreciate the significance of LCM in various fields. Remember, practice is key to solidifying your understanding. Try calculating the LCM of different number pairs to reinforce your learning and build your confidence. The more you practice, the more intuitive and efficient you'll become in finding the LCM of any set of numbers.
Latest Posts
Latest Posts
-
15 Minute Mile Marathon Time
Sep 20, 2025
-
Calculating The Mean In R
Sep 20, 2025
-
2x 2 5x 2 Factor
Sep 20, 2025
-
What Is A 77 Grade
Sep 20, 2025
-
144 Cm To Feet Inches
Sep 20, 2025
Related Post
Thank you for visiting our website which covers about Lcm Of 45 And 75 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.