Lcm Of 9 6 15
saludintensiva
Sep 13, 2025 · 7 min read
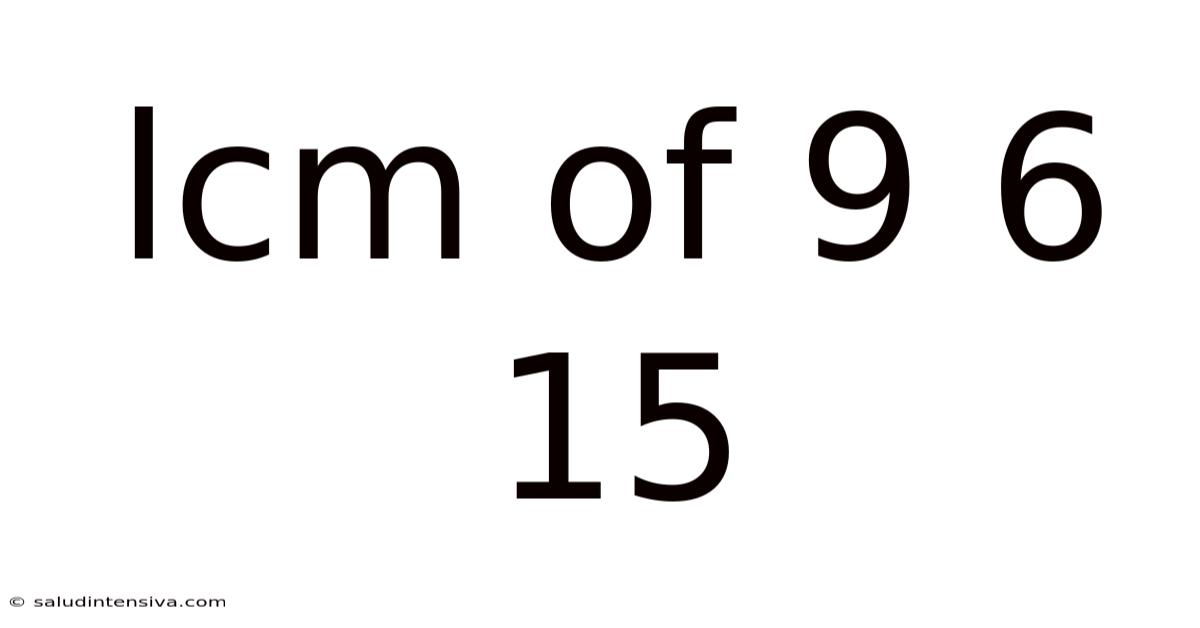
Table of Contents
Finding the LCM of 9, 6, and 15: A Comprehensive Guide
Finding the least common multiple (LCM) of a set of numbers is a fundamental concept in mathematics with applications spanning various fields, from scheduling tasks to understanding musical rhythms. This article provides a comprehensive guide to calculating the LCM of 9, 6, and 15, exploring different methods and delving into the underlying mathematical principles. We will explore multiple approaches, ensuring a solid understanding for students and anyone seeking a refresher on this important topic.
Understanding Least Common Multiple (LCM)
Before diving into the calculation, let's clarify what the LCM actually represents. The least common multiple of two or more numbers is the smallest positive integer that is divisible by all the given numbers without leaving any remainder. In simpler terms, it's the smallest number that all the numbers in the set can divide into evenly. This concept is crucial for various real-world applications, from calculating the smallest common denominator in fraction addition to determining the synchronization points in cyclical processes.
For example, let's consider the numbers 2 and 3. Multiples of 2 are 2, 4, 6, 8, 10, 12... and multiples of 3 are 3, 6, 9, 12, 15... The smallest number that appears in both lists is 6. Therefore, the LCM of 2 and 3 is 6.
Method 1: Listing Multiples
This is the most straightforward method, especially for smaller numbers. We list the multiples of each number until we find the smallest multiple common to all.
- Multiples of 9: 9, 18, 27, 36, 45, 54, 63, 72, 90, 108, 126, 135...
- Multiples of 6: 6, 12, 18, 24, 30, 36, 42, 48, 54, 60, 66, 72, 78, 84, 90, 96, 102, 108, 114, 120, 126, 132, 138…
- Multiples of 15: 15, 30, 45, 60, 75, 90, 105, 120, 135…
By comparing the lists, we can see that the smallest number appearing in all three lists is 90. Therefore, the LCM of 9, 6, and 15 is 90.
Method 2: Prime Factorization
This method is more efficient for larger numbers and provides a deeper understanding of the underlying mathematical principles. It involves finding the prime factorization of each number and then constructing the LCM using the highest powers of all prime factors present.
Let's find the prime factorization of each number:
- 9 = 3² (9 is 3 multiplied by 3)
- 6 = 2 × 3 (6 is 2 multiplied by 3)
- 15 = 3 × 5 (15 is 3 multiplied by 5)
Now, we identify the distinct prime factors present in these factorizations: 2, 3, and 5. For each prime factor, we select the highest power that appears in any of the factorizations:
- The highest power of 2 is 2¹ (from 6)
- The highest power of 3 is 3² (from 9)
- The highest power of 5 is 5¹ (from 15)
To find the LCM, we multiply these highest powers together:
LCM(9, 6, 15) = 2¹ × 3² × 5¹ = 2 × 9 × 5 = 90
Therefore, the LCM of 9, 6, and 15 is 90. This method is more systematic and less prone to error, especially when dealing with larger numbers or a greater number of numbers in the set.
Method 3: Using the Greatest Common Divisor (GCD)
There's a relationship between the LCM and the greatest common divisor (GCD) of two or more numbers. The product of the LCM and GCD of two numbers is equal to the product of the numbers themselves. This relationship can be extended to more than two numbers, although the calculation becomes slightly more complex.
First, let's find the GCD of 9, 6, and 15. We can use the Euclidean algorithm or prime factorization to do this. Using prime factorization:
- 9 = 3²
- 6 = 2 × 3
- 15 = 3 × 5
The only common prime factor is 3, and its lowest power is 3¹. Therefore, the GCD(9, 6, 15) = 3.
However, directly applying the LCM * GCD relationship to more than two numbers requires a more nuanced approach. While the formula LCM(a, b) * GCD(a, b) = a * b works for two numbers, it doesn't directly extend to three or more. Instead, we'd need to find the LCM of two numbers first, then find the LCM of the result with the third number, and so on. This makes the prime factorization method generally more efficient for multiple numbers.
Mathematical Explanation: Why Prime Factorization Works
The prime factorization method works because it systematically accounts for all the factors needed to create a common multiple. Prime numbers are the building blocks of all other integers; they are only divisible by 1 and themselves. By finding the prime factorization, we break down each number into its fundamental components. Then, by selecting the highest power of each prime factor, we ensure that the resulting number is divisible by all the original numbers. No smaller number can achieve this divisibility, hence it's the least common multiple. This method provides a robust and mathematically rigorous approach to finding the LCM, particularly advantageous when dealing with a larger number of integers or integers with numerous factors.
Real-World Applications of LCM
The concept of LCM has far-reaching applications beyond theoretical mathematics:
- Scheduling: Imagine two buses that arrive at a bus stop at different intervals. Finding the LCM of these intervals helps determine when both buses will arrive simultaneously.
- Fraction Addition: To add fractions with different denominators, you need to find the LCM of the denominators to obtain a common denominator.
- Music Theory: Rhythmic patterns and musical phrasing often rely on the LCM to determine points of synchronization and repetition.
- Gear Ratios: In mechanical engineering, LCM helps calculate the optimal gear ratios for smooth and efficient power transmission.
- Project Management: Determining when different phases of a project can be synchronized effectively often involves using the LCM.
Understanding LCM isn’t just about solving mathematical problems; it's about understanding underlying patterns and relationships that govern cyclical processes in various aspects of life.
Frequently Asked Questions (FAQ)
Q: What is the difference between LCM and GCD?
A: The least common multiple (LCM) is the smallest positive integer that is divisible by all the given numbers. The greatest common divisor (GCD) is the largest positive integer that divides all the given numbers without leaving a remainder. They are inversely related; the larger the GCD, the smaller the LCM, and vice versa.
Q: Can I use a calculator to find the LCM?
A: Many scientific calculators and online calculators have built-in functions to calculate the LCM of numbers. However, understanding the underlying methods is crucial for problem-solving and developing a deeper mathematical understanding.
Q: What if the numbers have no common factors?
A: If the numbers are relatively prime (meaning they share no common factors other than 1), their LCM is simply the product of the numbers.
Q: How do I find the LCM of more than three numbers?
A: The prime factorization method is the most efficient for finding the LCM of more than three numbers. You follow the same process: find the prime factorization of each number, identify the highest powers of each distinct prime factor, and multiply them together.
Conclusion
Finding the LCM of 9, 6, and 15, as demonstrated through multiple methods, underscores the importance of mastering fundamental mathematical concepts. While the listing method is suitable for smaller numbers, the prime factorization method offers a more powerful and efficient approach, particularly for larger numbers and a greater number of integers. Understanding LCM is not only crucial for solving mathematical problems but also for comprehending and applying mathematical concepts in various real-world scenarios. The practical applications extend far beyond the classroom, demonstrating the significance of this seemingly simple mathematical concept in various fields. By mastering this skill, you equip yourself with a valuable tool for tackling complex problems and understanding the underlying structure of numbers and their relationships.
Latest Posts
Latest Posts
-
Gcf Of 27 And 9
Sep 13, 2025
-
100 Days Ago From Today
Sep 13, 2025
-
1 1 Bar To Psi
Sep 13, 2025
-
Least Common Multiple Of Variables
Sep 13, 2025
-
Is 87 Prime Or Composite
Sep 13, 2025
Related Post
Thank you for visiting our website which covers about Lcm Of 9 6 15 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.