Negative 3 Divided By 3
saludintensiva
Sep 11, 2025 · 5 min read
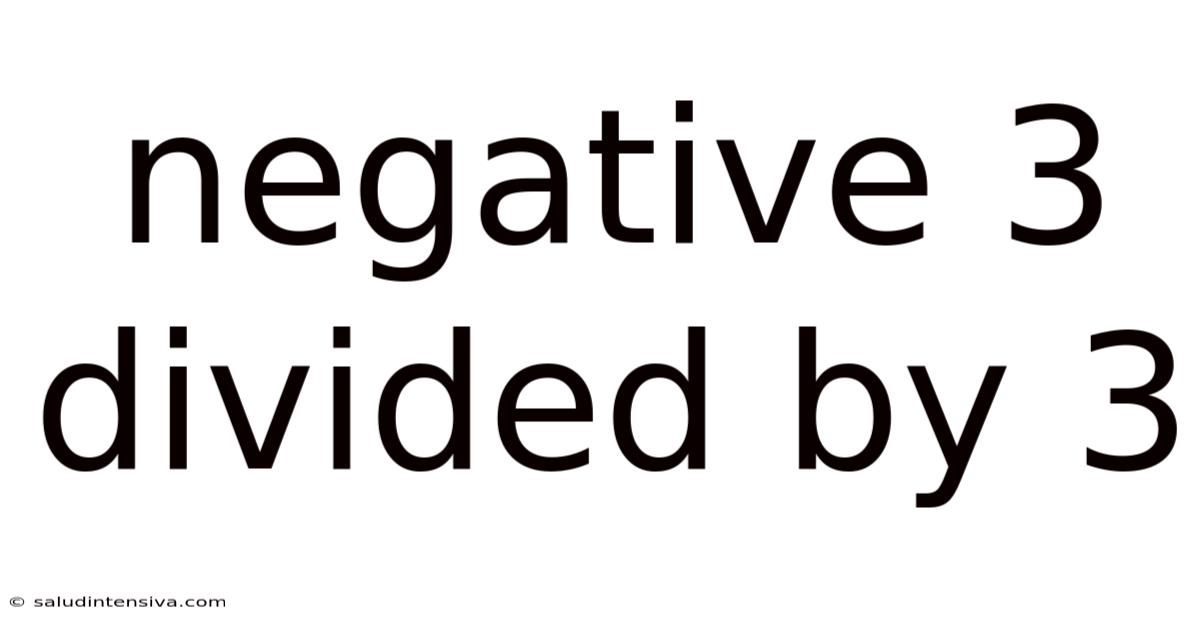
Table of Contents
Unraveling the Mystery: Negative 3 Divided by 3
Understanding basic arithmetic operations like division is fundamental to grasping more advanced mathematical concepts. This article delves into the seemingly simple calculation of -3 ÷ 3, exploring not only the answer but also the underlying principles of integer division and its applications. We'll cover the mechanics of the operation, explore the concept of negative numbers, and address common misconceptions to build a solid foundation in mathematical reasoning. This in-depth explanation will be suitable for students of all levels, from elementary school to high school, and even serve as a helpful refresher for adults.
Understanding the Components: Negative Numbers and Division
Before tackling the specific problem, let's refresh our understanding of the key components: negative numbers and division.
Negative Numbers: Negative numbers represent values less than zero. They are often used to represent quantities like debt, temperature below freezing, or a decrease in value. On the number line, they are located to the left of zero.
Division: Division is the inverse operation of multiplication. It essentially asks, "How many times does one number (the divisor) go into another number (the dividend)?" For example, 12 ÷ 3 = 4 because 3 goes into 12 four times (3 x 4 = 12).
Solving -3 ÷ 3: A Step-by-Step Approach
Now, let's tackle the problem: -3 ÷ 3. We can approach this problem in a few ways:
Method 1: Applying the Rules of Signs
When dividing integers with different signs (one positive and one negative), the result is always negative. This is a fundamental rule in mathematics. Therefore:
-3 ÷ 3 = -1
Method 2: Visual Representation
Imagine a number line. Start at -3. Division by 3 means we want to divide the interval from -3 to 0 into three equal parts. Each part represents -1. Therefore, -3 ÷ 3 = -1.
Method 3: Using Multiplication
Remember, division is the inverse of multiplication. We can check our answer by multiplying the quotient (-1) by the divisor (3):
-1 x 3 = -3
Since this matches our original dividend, our answer (-1) is correct.
The Significance of the Negative Sign
The negative sign in the result (-1) is crucial. It indicates that the division resulted in a value less than zero. This negative sign carries significant meaning depending on the context.
For example, if -3 represents a debt of 3 units and we divide it into 3 equal parts, each part represents a debt of 1 unit (-1). Or, if -3 represents a temperature of 3 degrees below zero, dividing it by 3 means each unit represents 1 degree below zero.
Expanding the Understanding: Different Scenarios and Applications
Let's explore various scenarios involving negative numbers and division to further solidify our understanding.
Scenario 1: Dividing a Negative Number by a Negative Number
Consider -3 ÷ -3. When dividing two negative numbers, the result is positive. This follows the rules of signs in multiplication and division:
-3 ÷ -3 = 1
Scenario 2: Dividing a Positive Number by a Negative Number
Consider 3 ÷ -3. Similar to our initial problem, dividing a positive number by a negative number results in a negative number:
3 ÷ -3 = -1
Scenario 3: Real-world Applications
The concept of dividing negative numbers has numerous real-world applications. Consider these examples:
- Finance: Calculating average daily losses in a business.
- Temperature: Determining the average hourly decrease in temperature.
- Altitude: Calculating the average rate of descent of an aircraft.
- Physics: Calculating average negative acceleration or deceleration.
In each of these examples, understanding how to correctly divide negative numbers is critical for accurate calculations and interpretations.
Addressing Common Misconceptions
Several misconceptions often arise when working with negative numbers and division:
Misconception 1: Ignoring the Negative Sign
Students may sometimes overlook the negative sign, leading to incorrect answers. Remember, the negative sign is an integral part of the number and must be considered during calculations.
Misconception 2: Confusing the Order of Operations
When dealing with multiple operations (addition, subtraction, multiplication, division), remember to follow the order of operations (PEMDAS/BODMAS). Division and multiplication are performed before addition and subtraction.
Misconception 3: Difficulty Visualizing Negative Numbers
Visualizing negative numbers on a number line can be helpful in understanding their meaning and how they behave in arithmetic operations.
Further Exploration: Beyond Basic Division
This foundational understanding of dividing negative numbers opens doors to more complex mathematical concepts:
- Algebra: Solving equations involving negative numbers and variables.
- Calculus: Understanding derivatives and integrals of functions with negative values.
- Statistics: Analyzing data sets with negative values, such as negative correlation.
Frequently Asked Questions (FAQ)
Q1: What happens if I divide 0 by -3?
A1: Dividing zero by any non-zero number always results in zero: 0 ÷ -3 = 0
Q2: What happens if I try to divide -3 by 0?
A2: Division by zero is undefined in mathematics. It's not possible to divide a number by zero.
Q3: Can I use a calculator to solve -3 ÷ 3?
A3: Yes, most calculators will correctly handle negative numbers and division, giving you the answer -1.
Q4: Is there a difference between -3/3 and (-3)/3?
A4: No, both expressions are equivalent and represent the same operation: -3 divided by 3, resulting in -1.
Conclusion: Mastering Negative Division
Understanding how to divide negative numbers is a crucial building block in mathematics. By applying the rules of signs and visualizing the operation, we can confidently solve problems involving negative numbers and division. This skill is essential for success in higher-level mathematics and various real-world applications. Remember the key rule: when dividing a negative number by a positive number, the result is always negative. This foundational knowledge serves as a strong base for future mathematical endeavors. Keep practicing, and you'll master this important concept in no time!
Latest Posts
Latest Posts
-
Gcf Of 12 And 10
Sep 11, 2025
-
Lcm Of 7 And 28
Sep 11, 2025
-
What Is 4 Of 35000
Sep 11, 2025
-
Using Density To Find Mass
Sep 11, 2025
-
What Does 3 2 Equal
Sep 11, 2025
Related Post
Thank you for visiting our website which covers about Negative 3 Divided By 3 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.