Negative 4 Minus Negative 7
saludintensiva
Sep 16, 2025 · 5 min read
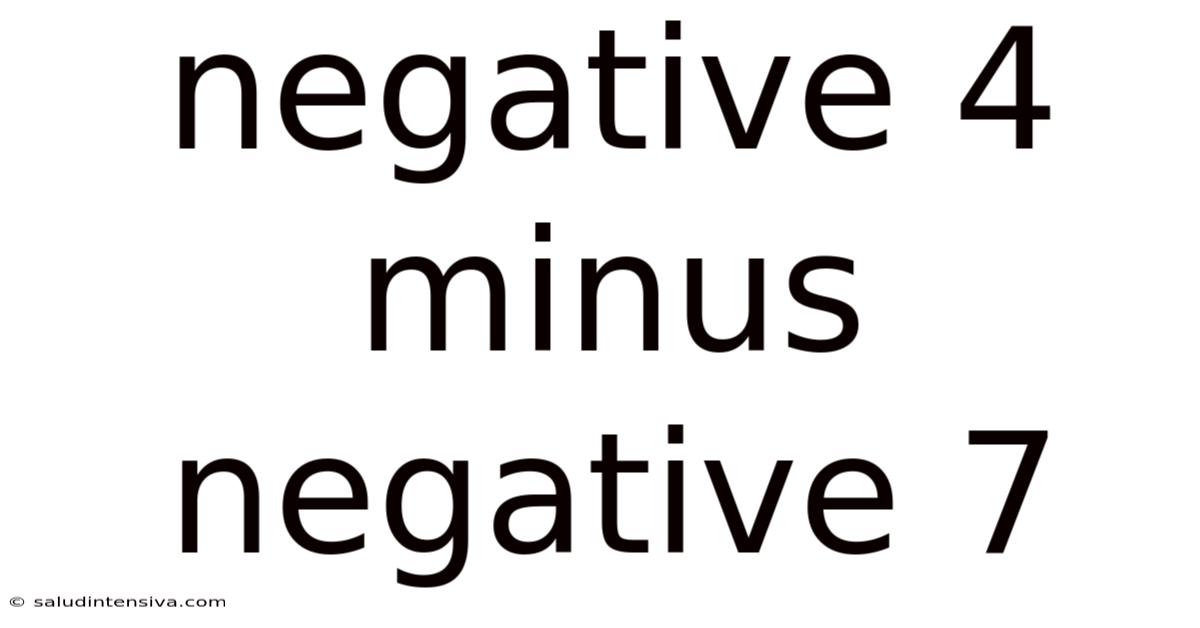
Table of Contents
Decoding the Mystery: Negative 4 Minus Negative 7
Understanding the concept of subtracting negative numbers can be tricky, even for those comfortable with basic arithmetic. This article will thoroughly explore the seemingly complex calculation of negative 4 minus negative 7, (-4 - (-7)), breaking down the process step-by-step and providing a solid foundation for understanding similar problems. We will delve into the underlying mathematical principles, offer practical examples, and address frequently asked questions to ensure a complete understanding of this concept. This will equip you with the skills to confidently tackle more advanced mathematical problems involving negative numbers.
Understanding Negative Numbers
Before diving into the problem at hand, let's solidify our understanding of negative numbers. Negative numbers represent values less than zero. They are often used to represent things like:
- Temperature: Temperatures below zero degrees Celsius or Fahrenheit.
- Debt or Loss: Financial losses or amounts owed.
- Coordinates: Positions on a coordinate plane that are below the x-axis or y-axis.
- Elevation: Points below sea level.
Visualizing negative numbers on a number line can be immensely helpful. The number line extends infinitely in both positive and negative directions. Zero is the midpoint, with positive numbers increasing to the right and negative numbers decreasing to the left.
The Rules of Subtracting Negative Numbers
Subtracting a negative number is equivalent to adding its positive counterpart. This seemingly counterintuitive rule is a fundamental concept in mathematics. The reason behind this lies in the definition of subtraction as the inverse of addition.
Think of subtraction as finding the difference between two numbers. If you subtract a negative number, you are essentially asking: "How much greater is the first number than the second (negative) number?" The difference will always be larger than the first number, resulting in addition.
The rule can be expressed formally as: a - (-b) = a + b
Where 'a' and 'b' represent any numbers.
Solving -4 - (-7) Step-by-Step
Now, let's apply this rule to our problem: -4 - (-7).
Step 1: Identify the numbers and the operation.
We have two numbers: -4 and -7. The operation is subtraction. Specifically, we are subtracting a negative number.
Step 2: Apply the rule of subtracting negative numbers.
Following the rule, subtracting a negative number is the same as adding its positive counterpart. Therefore, -4 - (-7) becomes -4 + 7.
Step 3: Perform the addition.
We now have a simple addition problem: -4 + 7. To solve this, consider the number line. Start at -4. Adding 7 means moving 7 units to the right on the number line.
This brings us to the point +3.
Step 4: State the solution.
Therefore, -4 - (-7) = 3
Visual Representation on a Number Line
Visualizing this on a number line reinforces the concept.
- Start at -4.
- Subtracting -7 means moving to the right 7 units (since we are subtracting a negative). Moving right on the number line represents adding positive values.
- You land on 3.
Mathematical Explanation: The Concept of Additive Inverses
The rule for subtracting negative numbers is deeply connected to the concept of additive inverses. The additive inverse of a number is the number that, when added to the original number, results in zero. For example:
- The additive inverse of 5 is -5 (because 5 + (-5) = 0).
- The additive inverse of -3 is 3 (because -3 + 3 = 0).
Subtracting a number is the same as adding its additive inverse. This is why subtracting a negative number is the same as adding its positive counterpart.
Practical Applications
Understanding the subtraction of negative numbers is crucial in various fields:
- Finance: Calculating profit and loss, especially when dealing with debts and credits.
- Physics: Dealing with vectors and displacement.
- Programming: Many programming languages use negative numbers extensively, and understanding their arithmetic is crucial for developing accurate programs.
- Engineering: In structural analysis or calculations involving negative forces.
- Everyday Life: Calculating changes in temperature, elevation changes, and more.
Expanding on the Concept: More Complex Problems
The principle we have learned can be extended to more complex calculations involving multiple negative numbers. Always remember to follow the order of operations (PEMDAS/BODMAS) and apply the rule for subtracting negative numbers systematically.
For example:
-10 - (-3) + (-5) - (-2)
- -10 - (-3) becomes -10 + 3 = -7
- -7 + (-5) becomes -7 - 5 = -12
- -12 - (-2) becomes -12 + 2 = -10
Therefore, -10 - (-3) + (-5) - (-2) = -10
Frequently Asked Questions (FAQ)
Q1: Why does subtracting a negative number result in addition?
A1: Subtracting a number is the same as adding its additive inverse. The additive inverse of a negative number is its positive counterpart.
Q2: Can I subtract a negative number from a negative number?
A2: Absolutely! The same rule applies. For instance, -5 - (-2) = -5 + 2 = -3
Q3: Is there a difference between -4 - 7 and -4 - (-7)?
A3: Yes, there's a significant difference. -4 - 7 = -11 (simple subtraction). -4 - (-7) = 3 (subtracting a negative number, which becomes addition).
Q4: How can I avoid making mistakes when subtracting negative numbers?
A4: Practice regularly. Use a number line to visualize the operation. Break down complex problems into smaller, manageable steps. Always remember the rule: subtracting a negative is the same as adding a positive.
Q5: Are there any real-world examples beyond finance and physics?
A5: Consider a scuba diver descending 10 meters (-10 meters) below sea level and then ascending 7 meters. Their final depth would be calculated as -10 - (-7) = -3 meters.
Conclusion
Subtracting negative numbers might seem intimidating initially, but by understanding the underlying principles and applying the simple rule of converting subtraction of a negative to addition of a positive, the process becomes straightforward. Mastering this concept provides a strong foundation for further mathematical explorations and is essential for success in various academic and professional fields. Through consistent practice and visual aids like number lines, you can build confidence and accuracy in tackling even the most complex calculations involving negative numbers. Remember to break down complex problems into smaller steps and systematically apply the rules. With sufficient practice, you will be able to effortlessly solve problems involving negative numbers with confidence and precision.
Latest Posts
Latest Posts
-
7 1 3 Improper Fraction
Sep 16, 2025
-
2 Out Of 13 Percentage
Sep 16, 2025
-
How Much Percent Is 1 4
Sep 16, 2025
-
Inch 2 To Ft 2
Sep 16, 2025
-
5 8 Divided By 2
Sep 16, 2025
Related Post
Thank you for visiting our website which covers about Negative 4 Minus Negative 7 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.