Simplify -1 -i I 1
saludintensiva
Sep 19, 2025 · 7 min read
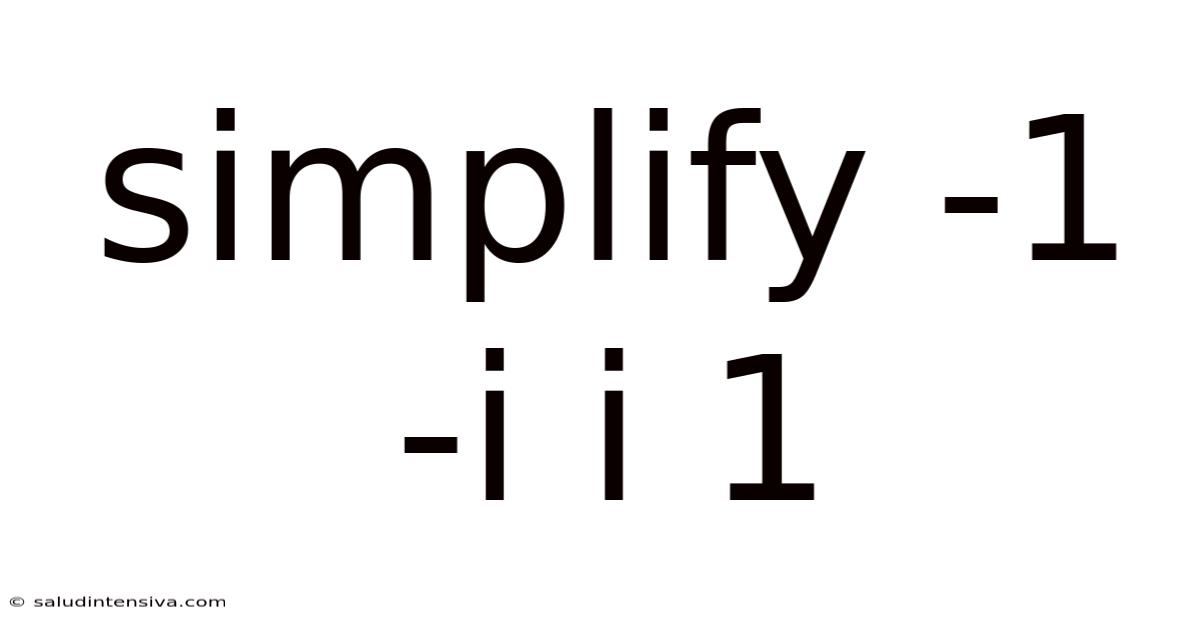
Table of Contents
Simplifying Complex Numbers: A Deep Dive into -1, -i, i, and 1
This article explores the simplification of complex numbers, specifically focusing on the four key elements: -1, -i, i, and 1. We'll delve into their representation on the complex plane, their relationships to each other, and various methods for simplifying expressions involving these fundamental components. Understanding these concepts is crucial for mastering complex number arithmetic and its applications in various fields like electrical engineering, quantum mechanics, and signal processing.
Introduction to Complex Numbers
Before diving into the simplification process, let's establish a solid foundation. A complex number is a number that can be expressed in the form a + bi, where 'a' and 'b' are real numbers, and 'i' is the imaginary unit. The imaginary unit 'i' is defined as the square root of -1, i.e., i² = -1. This seemingly simple definition opens up a whole new world of mathematical possibilities.
The term 'imaginary' might be misleading; these numbers are not "less real" than real numbers. They're essential for solving equations that don't have solutions within the realm of real numbers alone. For instance, the equation x² + 1 = 0 has no real solutions, but it has two complex solutions: x = i and x = -i.
In the expression a + bi, 'a' is called the real part and 'b' is called the imaginary part. When b = 0, the complex number is simply a real number. When a = 0, the complex number is a purely imaginary number.
Representing Complex Numbers on the Complex Plane
The complex plane (also known as the Argand plane) provides a visual representation of complex numbers. The horizontal axis represents the real part (a), and the vertical axis represents the imaginary part (b). Each complex number a + bi can be plotted as a point (a, b) on this plane.
This visual representation is invaluable for understanding operations involving complex numbers, especially when dealing with their magnitudes and arguments (polar form).
The Four Key Players: -1, -i, i, and 1
Now let's focus on the four specific complex numbers mentioned in the title: -1, -i, i, and 1. These are fundamental building blocks in the world of complex numbers.
-
1: This is the multiplicative identity in both real and complex numbers. It's located at (1, 0) on the complex plane.
-
-1: The additive inverse of 1, it's located at (-1, 0) on the complex plane. It represents a rotation of 180 degrees around the origin on the complex plane.
-
i: The imaginary unit, located at (0, 1) on the complex plane. It represents a 90-degree counterclockwise rotation from 1.
-
-i: The additive inverse of i, located at (0, -1) on the complex plane. It represents a 90-degree clockwise rotation from 1, or a 270-degree counterclockwise rotation.
The relationship between these four numbers is cyclic and intimately tied to the definition of 'i'. Multiplying by 'i' results in a 90-degree counterclockwise rotation on the complex plane.
- 1 * i = i
- i * i = i² = -1
- -1 * i = -i
- -i * i = -i² = 1
This cycle repeats continuously: multiplying by i repeatedly rotates the number 90 degrees counterclockwise around the origin.
Simplifying Expressions Involving -1, -i, i, and 1
Simplifying expressions involving these four numbers often involves applying the fundamental rules of complex number arithmetic, particularly the properties of 'i'. Here are some examples:
-
Example 1: Simplify (2i) * (-3i)
This involves multiplying the real coefficients and the imaginary parts: 2 * -3 * i * i = -6i² = -6(-1) = 6
-
Example 2: Simplify (1 + i) + (-1 - i)
This simplifies to (1 - 1) + (i - i) = 0
-
Example 3: Simplify (3 + 2i) * (1 - i)
Here we need to use the distributive property (FOIL): 3(1) + 3(-i) + 2i(1) + 2i(-i) = 3 - 3i + 2i - 2i² = 3 - i - 2(-1) = 3 - i + 2 = 5 - i
-
Example 4: Simplify (1/i)
To simplify this, we multiply the numerator and denominator by the conjugate of the denominator (which is -i): (1/i) * (-i/-i) = -i/(-i²) = -i/1 = -i
-
Example 5: Simplify ( (2 + 3i) / (1 + i) )
We multiply both the numerator and the denominator by the complex conjugate of the denominator (1 - i):
( (2 + 3i) / (1 + i) ) * ( (1 - i) / (1 - i) ) = ( (2 + 3i)(1 - i) ) / ( (1 + i)(1 - i) ) = ( 2 - 2i + 3i - 3i² ) / ( 1 - i² ) = ( 2 + i + 3 ) / ( 1 + 1 ) = ( 5 + i ) / 2 = 5/2 + (1/2)i
These examples illustrate the basic techniques for simplifying expressions involving -1, -i, i, and 1. The key is to remember the definition of i (i² = -1) and utilize the distributive property and the concept of complex conjugates effectively.
Powers of i
Understanding the powers of i is also crucial for simplification. The pattern repeats every four powers:
- i¹ = i
- i² = -1
- i³ = i² * i = -i
- i⁴ = (i²)² = (-1)² = 1
- i⁵ = i⁴ * i = 1 * i = i
- i⁶ = i⁴ * i² = 1 * -1 = -1
- i⁷ = i⁴ * i³ = 1 * -i = -i
- i⁸ = (i⁴)² = 1² = 1
and so on. This cyclical pattern allows us to simplify any power of 'i' by finding its remainder when divided by 4. For example, i¹⁷ = i¹⁶ * i = (i⁴)⁴ * i = 1⁴ * i = i.
Euler's Formula and its Relation to -1, -i, i, and 1
Euler's formula, e^(ix) = cos(x) + i sin(x), establishes a profound connection between exponential functions, trigonometric functions, and complex numbers. This formula allows for an elegant representation of complex numbers in polar form. When applied to our four key numbers, we find:
- e^(i0) = cos(0) + i sin(0) = 1
- e^(iπ) = cos(π) + i sin(π) = -1 (This is famously known as Euler's identity: e^(iπ) + 1 = 0)
- e^(iπ/2) = cos(π/2) + i sin(π/2) = i
- e^(-iπ/2) = cos(-π/2) + i sin(-π/2) = -i
Euler's formula provides a more holistic understanding of the geometric interpretation of complex numbers and their relationships, emphasizing the cyclical nature of multiplication by i.
Applications of Complex Numbers
The simplicity of -1, -i, i, and 1 belies their profound impact across numerous scientific and engineering fields. Complex numbers are invaluable in:
-
Electrical Engineering: Analyzing alternating current circuits, where 'i' represents the imaginary part related to impedance and reactance.
-
Quantum Mechanics: Describing wave functions and quantum states, which are often expressed using complex numbers.
-
Signal Processing: Representing and manipulating signals in the frequency domain using Fourier transforms, which heavily rely on complex numbers.
-
Fluid Dynamics: Solving equations related to fluid flow and turbulence.
-
Control Systems: Designing and analyzing control systems for various applications.
Frequently Asked Questions (FAQ)
Q: What is the difference between a real number and a complex number?
A: A real number is a number that can be plotted on a number line (e.g., 1, -2, 0, π). A complex number includes a real part and an imaginary part, and can be plotted on a complex plane.
Q: Why is 'i' called the imaginary unit?
A: The term "imaginary" is historical and can be slightly misleading. It simply signifies that 'i' is not a real number, but it is a crucial part of the complex number system. It's a perfectly valid mathematical concept with real-world applications.
Q: How can I visualize complex numbers?
A: The complex plane is the best way to visualize complex numbers. The horizontal axis represents the real part, and the vertical axis represents the imaginary part. Each complex number can be represented as a point on this plane.
Q: Are all complex numbers expressible in the form a + bi?
A: Yes, all complex numbers can be expressed in this rectangular form, although other forms, such as polar form, are also useful.
Q: What is the conjugate of a complex number?
A: The conjugate of a complex number a + bi is a - bi. It's obtained by changing the sign of the imaginary part. Complex conjugates are useful in various operations, including division of complex numbers.
Conclusion
Simplifying expressions involving -1, -i, i, and 1, the fundamental building blocks of complex numbers, relies on understanding the definition of the imaginary unit 'i' (i² = -1) and the properties of complex numbers. Through consistent application of the basic rules of arithmetic and the use of complex conjugates when necessary, we can effectively simplify expressions and navigate the world of complex number calculations. This understanding forms a crucial base for more advanced applications of complex numbers across diverse scientific and engineering disciplines. The seemingly simple arithmetic of these four numbers unlocks a vast landscape of mathematical possibilities and real-world applications, demonstrating the power and elegance of the complex number system.
Latest Posts
Latest Posts
-
Sum Of Five Squares Calculator
Sep 20, 2025
-
All The Factors Of 42
Sep 20, 2025
-
How Big Is 2 Yards
Sep 20, 2025
-
60 Days After June 21
Sep 20, 2025
-
What Is 65 In Celsius
Sep 20, 2025
Related Post
Thank you for visiting our website which covers about Simplify -1 -i I 1 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.