Solve 1 4 5 4
saludintensiva
Sep 13, 2025 · 5 min read
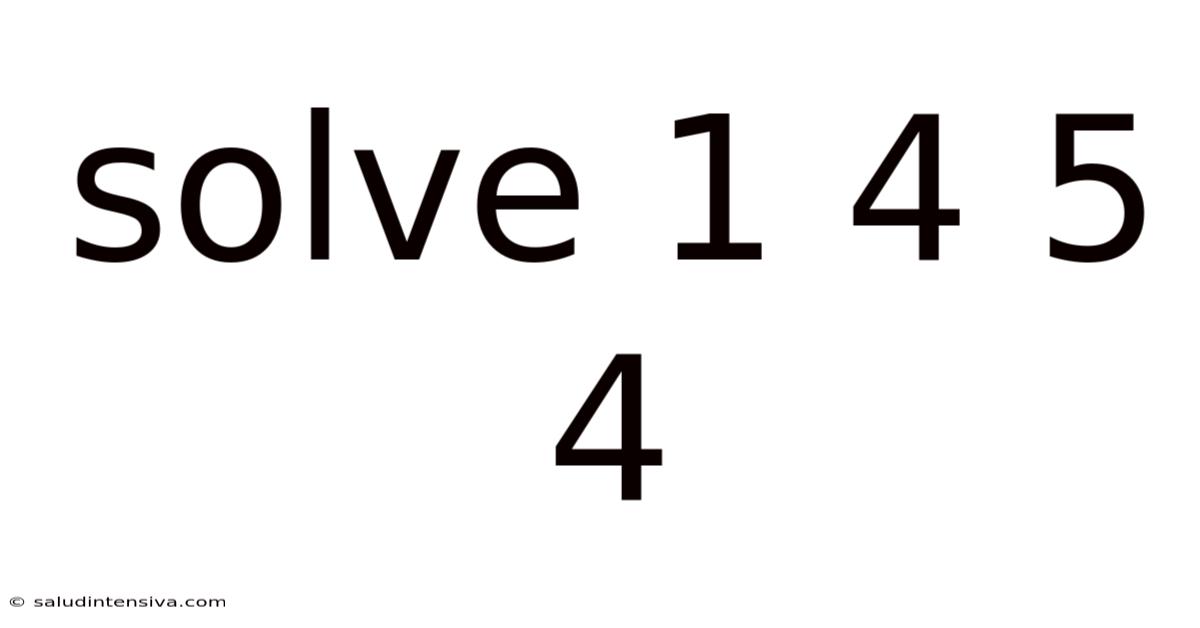
Table of Contents
Decoding the Puzzle: Solving "1 4 5 4" and Unveiling Mathematical Patterns
The seemingly simple sequence "1 4 5 4" might appear innocuous at first glance. However, this numerical puzzle, often presented as a riddle or a brain teaser, opens doors to a fascinating exploration of mathematical patterns, logical reasoning, and problem-solving techniques. This article delves deep into various approaches to solve this puzzle, explaining the underlying logic, exploring potential solutions, and addressing frequently asked questions. We'll uncover not just a solution, but multiple perspectives that illuminate the rich world of mathematical thinking.
Understanding the Challenge: What Makes "1 4 5 4" Unique?
The beauty of puzzles like "1 4 5 4" lies in their ambiguity. Unlike straightforward arithmetic problems, this sequence doesn't immediately suggest a single, obvious operation. The challenge lies in identifying the hidden rule or pattern that connects these numbers. This ambiguity allows for multiple interpretations and encourages creative problem-solving strategies, fostering critical thinking and mathematical intuition. The absence of explicit instructions invites exploration of various mathematical concepts, making it an excellent exercise for developing analytical skills.
Approach 1: Exploring Number Relationships and Patterns
One of the most common approaches is to look for relationships between the numbers themselves. Let's examine the sequence: 1, 4, 5, 4.
- Differences: Calculating the differences between consecutive numbers reveals a pattern:
- 4 - 1 = 3
- 5 - 4 = 1
- 4 - 5 = -1
This difference sequence (3, 1, -1) doesn't immediately reveal an obvious mathematical pattern. However, it highlights the fluctuating nature of the relationship between the numbers.
-
Ratios: Examining the ratios between consecutive numbers also yields no clear pattern:
- 4/1 = 4
- 5/4 = 1.25
- 4/5 = 0.8
-
Squares and Cubes: Considering the squares or cubes of the numbers also doesn't lead to a discernible pattern.
This initial exploration suggests that a simpler arithmetic relationship might not be the solution. We need to consider alternative approaches.
Approach 2: Considering Number Properties and Operations
Let's explore beyond basic arithmetic operations and delve into the properties of numbers:
- Digit Sums: Adding the digits of each number yields:
- 1: 1
- 4: 4
- 5: 5
- 4: 4
This approach doesn't immediately produce a clear pattern either.
-
Prime Numbers and Divisibility: Analyzing the sequence in terms of prime numbers or divisibility rules doesn't reveal an obvious pattern.
-
Combinatorial Approaches: Could there be a combinatorial element to this sequence? Is there a way to arrange or manipulate the numbers to reveal a pattern? This requires more sophisticated analysis and might involve exploring permutations or combinations.
Approach 3: The "Next Number" Approach and Extrapolation
Many puzzle solvers try to determine the next number in the sequence. This approach relies on extrapolating the identified pattern to predict the subsequent number. However, without a clearly defined pattern using basic arithmetic, this is difficult. The lack of an easily discernible pattern underscores the need for a more creative or abstract approach.
Approach 4: Introducing the Concept of Symbolic Representation
A more advanced approach involves abstracting the numbers beyond their numerical values. Let's consider interpreting the numbers as symbols or elements in a system:
-
Representing digits as shapes: We could assign shapes to each number. For example, 1 could be a single dot, 4 a square, and 5 a pentagon. This might reveal a spatial or geometric pattern. However, without additional context, this remains speculative.
-
Representational Systems: The sequence could be representing something entirely different. Perhaps it's a code, a cipher, or a reference to a specific system. For example, 1, 4, 5, 4 might be representing a sequence of events, steps in a process, or elements within a structure.
This approach highlights the potential for multiple solutions depending on the chosen interpretation framework. Without additional clues or context, the possibilities are vast.
Approach 5: Thinking Outside the Box: Context Matters
The crucial aspect often missing in solving puzzles like "1 4 5 4" is the context. Where did you encounter this sequence? What was the surrounding information? The solution may heavily rely on the context in which the puzzle is presented.
Example Contextual Applications:
-
Music Theory: The numbers could represent musical notes, intervals, or rhythmic patterns. In this context, the sequence would need to be interpreted within the specific rules and conventions of music theory.
-
Game Design: It could be a step-by-step sequence in a game, where each number represents an action or event.
-
Coding/Programming: Within a programming context, it could be a simplified code or data sequence, with the numbers representing states, variables, or instructions.
Frequently Asked Questions (FAQ)
Q: Is there only one correct answer to this puzzle?
A: No. The inherent ambiguity of "1 4 5 4" allows for multiple interpretations and potential solutions. The "correct" answer depends heavily on the context in which the puzzle is presented. Without further information, any well-justified solution based on a consistent pattern or logical argument could be considered valid.
Q: How can I improve my problem-solving skills for these types of puzzles?
A: Practice is key! Engage regularly with puzzles and brain teasers, exploring different approaches and expanding your mathematical knowledge. Focus on developing your analytical and critical thinking skills. Consider studying number theory, combinatorics, and logic to deepen your understanding of mathematical patterns and relationships.
Q: What are some resources to help me learn more about mathematical problem-solving?
A: Numerous online resources, books, and courses are available to enhance mathematical problem-solving skills. Look for resources focusing on mathematical puzzles, logic games, and introductory number theory.
Conclusion: Embracing the Ambiguity and the Journey
The puzzle "1 4 5 4" serves as a powerful illustration of how a seemingly simple numerical sequence can spark a rich exploration of mathematical concepts, logical reasoning, and creative problem-solving. The absence of a single, definitive solution underscores the importance of contextual understanding and encourages diverse perspectives. The true value of this type of puzzle lies not just in finding a solution but in the process of exploration, the development of analytical thinking, and the realization that multiple interpretations can be equally valid. The journey of uncovering potential patterns and exploring various approaches is as valuable as finding a "correct" answer. It's an excellent exercise in fostering creativity, critical thinking, and enhancing mathematical fluency. The lack of a readily apparent solution challenges us to think beyond conventional arithmetic and embrace the beauty of mathematical ambiguity.
Latest Posts
Latest Posts
-
50 Deg C To Fahrenheit
Sep 13, 2025
-
35 60 As A Percentage
Sep 13, 2025
-
Lcm Of 10 And 2
Sep 13, 2025
-
31 Days Ago From Today
Sep 13, 2025
-
1 3 To The 2nd Power
Sep 13, 2025
Related Post
Thank you for visiting our website which covers about Solve 1 4 5 4 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.