Solve For X 2 8
saludintensiva
Sep 21, 2025 · 6 min read
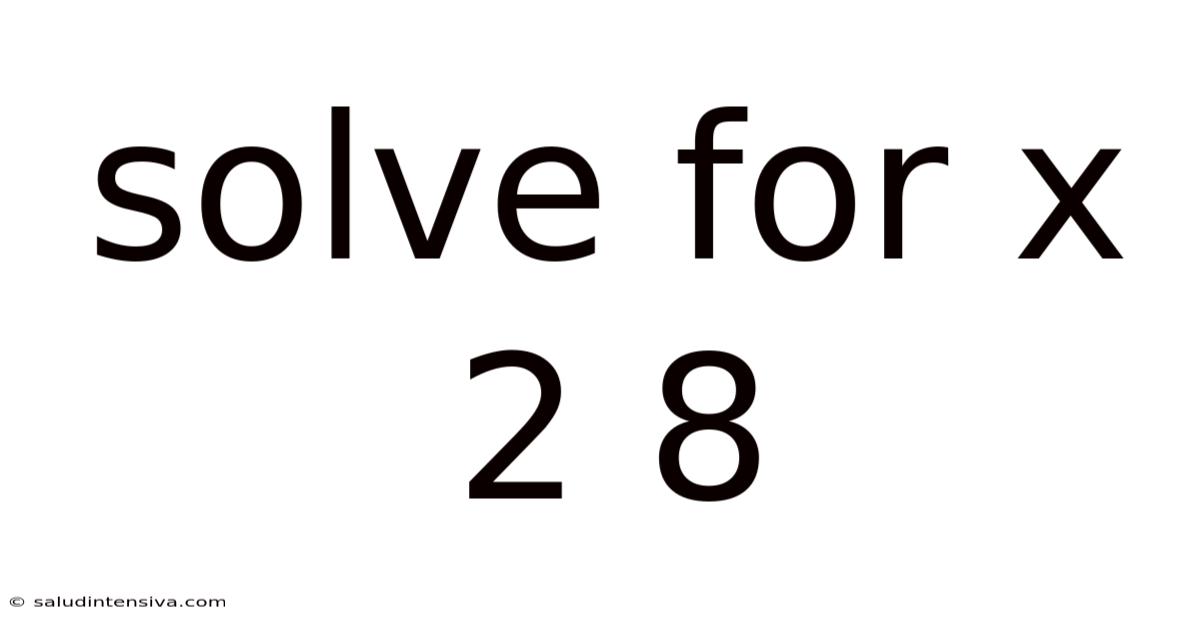
Table of Contents
Solving for x: A Deep Dive into the Equation 2x = 8
This article provides a comprehensive guide on how to solve the simple algebraic equation 2x = 8, explaining the underlying principles and demonstrating various approaches. We'll delve into the core concepts of algebra, explore different methods of solving for 'x', and address common misconceptions. This will be valuable for students learning basic algebra, and also serves as a refresher for those who may have forgotten the fundamentals. By the end, you'll not only know the answer but also understand the why behind the solution, building a stronger foundation in algebraic thinking.
Introduction: Understanding the Basics
Before we jump into solving 2x = 8, let's briefly review some fundamental algebraic concepts. An equation is a mathematical statement asserting the equality of two expressions. In this case, our equation is 2x = 8. The "x" represents an unknown variable, a value we need to find. The "2" is the coefficient of x, indicating that x is multiplied by 2. The "8" is a constant, a fixed value. Our goal is to isolate 'x' on one side of the equation to determine its value.
Method 1: Using the Inverse Operation
The most straightforward method to solve 2x = 8 involves using the inverse operation. The inverse operation is the opposite mathematical operation that "undoes" the original operation. Since 'x' is being multiplied by 2, the inverse operation is division by 2. We apply this to both sides of the equation to maintain balance:
2x = 8
2x / 2 = 8 / 2
x = 4
Therefore, the solution to the equation 2x = 8 is x = 4. This approach highlights a crucial principle in algebra: whatever operation you perform on one side of the equation, you must perform on the other side to maintain equality.
Method 2: Applying the Division Property of Equality
The previous method implicitly used the division property of equality, a fundamental rule in algebra. The division property of equality states that if you divide both sides of an equation by the same non-zero number, the resulting equation remains equal. In our case, we divided both sides of 2x = 8 by 2, resulting in x = 4. This property is essential for solving a wide range of algebraic equations.
Method 3: Using a visual representation (for beginners)
For those who find abstract equations challenging, visualizing the problem can be helpful. Imagine you have two identical groups of objects, and together they total eight objects. How many objects are in each group? The answer is clearly four. This intuitive approach mirrors the algebraic solution: 2 groups (2x) = 8 objects, therefore, 1 group (x) = 4 objects. This method can be helpful for beginners to grasp the concept before moving to symbolic manipulation.
Expanding the Concept: Solving Similar Equations
Understanding the solution to 2x = 8 allows us to extend our knowledge to solve similar equations. Let's consider a few examples:
- 3x = 15: Applying the inverse operation (division by 3) gives us x = 5.
- 5x = 25: Dividing both sides by 5 yields x = 5.
- 7x = -14: Dividing both sides by 7 results in x = -2. (Note: This introduces negative numbers, further expanding the application of the concept).
- -2x = 10: Dividing both sides by -2 gives us x = -5 (Remember: a negative divided by a negative results in a positive).
These examples demonstrate the versatility of the inverse operation method and the division property of equality in solving various linear equations. The core principle remains the same: isolate the variable 'x' by performing the inverse operation on both sides of the equation.
Understanding the concept of Variables and Constants
Let's take a moment to emphasize the importance of understanding the roles of variables and constants in equations. In the equation 2x = 8, 'x' is the variable – its value is unknown and what we aim to find. The '2' and '8' are constants – their values are fixed and unchanging. Differentiating between variables and constants is crucial for understanding and manipulating algebraic expressions.
Solving Equations with More Complex Operations: A Gentle Introduction
While 2x = 8 is a very simple equation, the principles we've discussed form the foundation for solving more complex equations. Let's consider a slightly more challenging example to illustrate this:
3x + 5 = 14
To solve this, we need to follow a series of steps:
-
Isolate the term with 'x': Subtract 5 from both sides of the equation: 3x + 5 - 5 = 14 - 5 3x = 9
-
Solve for 'x': Divide both sides by 3: 3x / 3 = 9 / 3 x = 3
This example demonstrates a multi-step process, involving both subtraction and division, but the underlying principles remain the same. We use inverse operations to isolate the variable and maintain the equality of the equation.
Dealing with Fractions: Another Level Up
Let's explore another common scenario: solving equations involving fractions. Consider the equation:
(1/2)x = 4
To solve this, we can again use the inverse operation. The inverse of multiplying by (1/2) is multiplying by its reciprocal, which is 2/1 (or simply 2).
(1/2)x = 4
(1/2)x * 2 = 4 * 2
x = 8
This demonstrates that the same fundamental principles apply even when dealing with fractions. The key is to understand and apply the correct inverse operation to isolate the variable.
The Importance of Checking your Solutions
After solving for 'x', it's always good practice to check your solution by substituting the value back into the original equation. In the case of 2x = 8, substituting x = 4 gives us:
2(4) = 8
8 = 8
Since the equation holds true, our solution is correct. This step helps identify potential errors and builds confidence in your algebraic skills.
Frequently Asked Questions (FAQ)
-
Q: What if the coefficient of x is a decimal?
A: The same principles apply. For instance, if you have 0.5x = 10, you would divide both sides by 0.5 to solve for x.
-
Q: What if 'x' is on both sides of the equation?
A: You would first manipulate the equation to bring all terms containing 'x' to one side and all constant terms to the other side, then proceed with the inverse operation.
-
Q: What if the equation involves more than one variable?
A: Equations with more than one variable require more advanced algebraic techniques, such as substitution or elimination. These are topics for more advanced algebra courses.
-
Q: What happens if I divide by zero?
A: Dividing by zero is undefined in mathematics, so it's crucial to avoid dividing both sides of an equation by a variable or expression that could potentially be zero.
Conclusion: Mastering the Fundamentals
Solving for 'x' in simple equations like 2x = 8 forms the bedrock of algebraic understanding. Mastering these fundamental concepts—understanding variables and constants, employing inverse operations, and applying the properties of equality—provides a solid foundation for tackling more complex algebraic problems. Remember to practice regularly, check your solutions, and don't hesitate to explore different approaches until you find the method that best suits your learning style. By consistently applying these principles, you'll build confidence and proficiency in algebra. The seemingly simple equation 2x = 8 opens doors to a vast world of mathematical possibilities.
Latest Posts
Latest Posts
-
Convert 45 Pounds To Kilograms
Sep 21, 2025
-
Random Number Generator 1 18
Sep 21, 2025
-
Thwyl Mn Kylw Ala Bawnd
Sep 21, 2025
-
Days Until August 1 2025
Sep 21, 2025
-
14 Grados Farenheit A Centigrados
Sep 21, 2025
Related Post
Thank you for visiting our website which covers about Solve For X 2 8 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.