Square Root Of 10 000
saludintensiva
Sep 09, 2025 · 5 min read
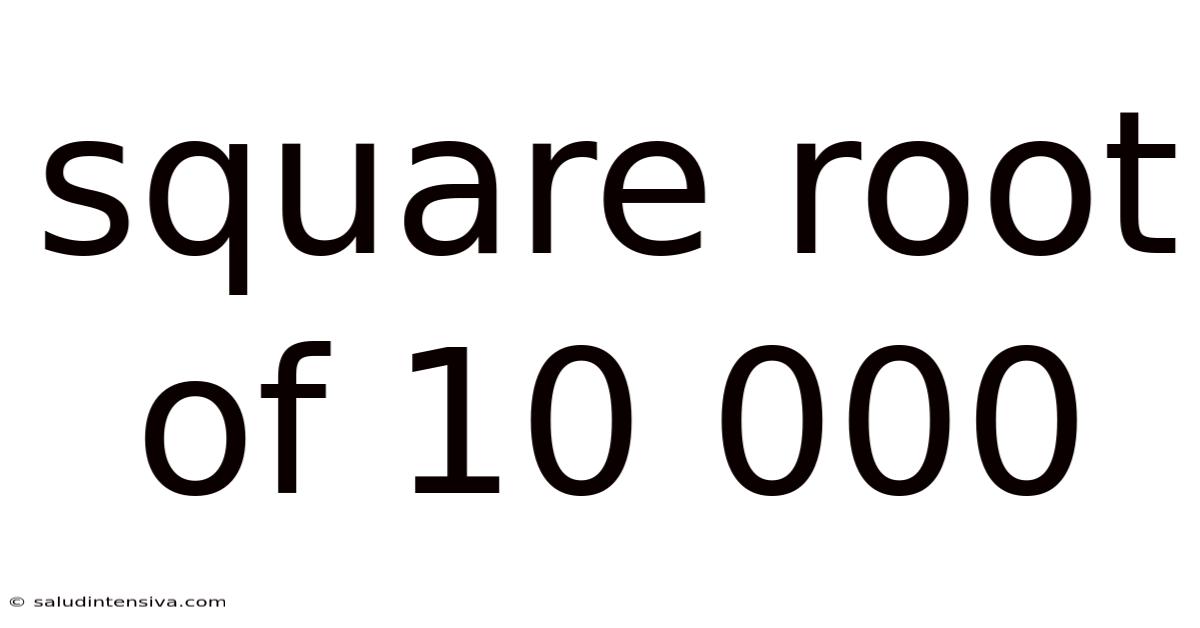
Table of Contents
Unveiling the Mystery: Understanding the Square Root of 10,000
Finding the square root of 10,000 might seem like a simple mathematical task, especially for those comfortable with basic arithmetic. However, delving deeper reveals a fascinating journey into the core concepts of square roots, their applications in various fields, and the broader implications of understanding numerical relationships. This article will not only provide the answer but also explain the underlying principles, explore different methods of calculation, and discuss the relevance of square roots in real-world scenarios. Understanding the square root of 10,000 opens doors to a richer comprehension of mathematics and its power.
What is a Square Root?
Before diving into the specifics of the square root of 10,000, let's establish a solid foundation. A square root is a number that, when multiplied by itself (squared), produces a given number. In simpler terms, it's the inverse operation of squaring a number. For example, the square root of 9 (√9) is 3, because 3 x 3 = 9. Similarly, the square root of 16 (√16) is 4, since 4 x 4 = 16. The square root symbol (√) is used to denote this operation.
Calculating the Square Root of 10,000: The Direct Approach
The most straightforward method to find the square root of 10,000 is to consider the definition. We're looking for a number that, when multiplied by itself, equals 10,000. Through a bit of mental arithmetic or a simple calculator, we quickly arrive at the answer:
√10,000 = 100
Because 100 x 100 = 10,000.
Understanding the Logic: Prime Factorization and Exponents
A deeper understanding can be achieved by employing prime factorization. Prime factorization is the process of breaking down a number into its prime factors – numbers that are only divisible by 1 and themselves (e.g., 2, 3, 5, 7, etc.).
Let's factorize 10,000:
10,000 = 10 x 10 x 10 x 10 = (2 x 5) x (2 x 5) x (2 x 5) x (2 x 5) = 2<sup>4</sup> x 5<sup>4</sup>
Now, to find the square root, we take half of each exponent:
√(2<sup>4</sup> x 5<sup>4</sup>) = 2<sup>(4/2)</sup> x 5<sup>(4/2)</sup> = 2<sup>2</sup> x 5<sup>2</sup> = 4 x 25 = 100
This method not only confirms our earlier answer but also illuminates the relationship between exponents and square roots. It demonstrates that finding the square root is essentially about halving the exponents in the prime factorization.
Beyond the Basics: Exploring Different Calculation Methods
While the direct approach and prime factorization are sufficient for finding the square root of 10,000, let's explore other methods that are applicable to a broader range of numbers.
-
Using a Calculator: Most scientific calculators have a dedicated square root function (√). Simply input 10,000 and press the square root button to obtain the answer instantly. This is particularly useful for larger numbers where mental calculations become challenging.
-
Long Division Method: This is a more manual method suitable for numbers without readily apparent square roots. The algorithm involves a series of iterative steps to progressively refine an approximation of the square root. While effective, it’s more complex and time-consuming than the methods discussed earlier for a number like 10,000.
-
Newton-Raphson Method: This is a powerful iterative numerical method for finding successively better approximations of the roots of a real-valued function. It's particularly useful for finding square roots of numbers that don't have exact integer square roots. While efficient for complex calculations, it’s beyond the scope of this simplified explanation for the square root of 10,000.
Real-World Applications: Where Square Roots Matter
The seemingly simple concept of square roots has far-reaching applications across various disciplines. Understanding square roots is crucial in:
-
Geometry: Calculating the hypotenuse of a right-angled triangle using the Pythagorean theorem (a² + b² = c²) requires finding the square root. This has countless applications in construction, surveying, and navigation.
-
Physics: Many physical phenomena involve square roots. For instance, calculating the velocity of an object based on its kinetic energy involves the square root. Similarly, understanding wave propagation and other oscillatory phenomena requires an understanding of square roots.
-
Statistics: Standard deviation, a crucial measure of data dispersion, involves calculating the square root of the variance. This is fundamental in statistical analysis and data interpretation.
-
Engineering: From designing bridges to building skyscrapers, engineers frequently utilize square roots in calculations related to stress, strain, and structural integrity. The concept is essential for ensuring safety and stability in various engineering projects.
-
Finance: Compound interest calculations and determining investment returns often rely on square roots. Understanding these calculations is crucial for financial planning and investment analysis.
Frequently Asked Questions (FAQ)
- Q: Is there a negative square root of 10,000?
A: Technically, yes. Both 100 and -100, when squared, result in 10,000. However, when we refer to the square root, we generally mean the principal square root, which is the non-negative value (100 in this case).
- Q: How do I calculate the square root of a non-perfect square (e.g., √2)?
A: For non-perfect squares, you can use a calculator, employ iterative numerical methods like the Newton-Raphson method, or utilize approximations based on known square roots.
- Q: What are cube roots and higher-order roots?
A: While this article focuses on square roots, it's important to note that cube roots (∛), fourth roots (∜), and higher-order roots exist. These represent numbers that, when multiplied by themselves a certain number of times, produce a given number. For example, the cube root of 8 (∛8) is 2 because 2 x 2 x 2 = 8.
- Q: Are there any online tools or software for calculating square roots?
A: Yes, numerous online calculators and mathematical software packages are available that can compute square roots efficiently and accurately for any number.
Conclusion: Beyond the Number 100
The square root of 10,000 is simply 100. However, this seemingly straightforward calculation opens up a world of mathematical understanding. By exploring the underlying principles, examining different calculation methods, and appreciating the diverse real-world applications, we gain a richer and more complete appreciation of the power and significance of square roots in mathematics and beyond. This understanding is fundamental for progress in many scientific and technological fields and contributes to a broader, more insightful comprehension of the numerical world around us. The journey from a simple calculation to a deeper understanding is the true essence of mathematical exploration.
Latest Posts
Latest Posts
-
What Was 12 Weeks Ago
Sep 09, 2025
-
Gcf Of 40 And 36
Sep 09, 2025
-
Lcm Of 28 And 42
Sep 09, 2025
-
2 To The Fifth Power
Sep 09, 2025
-
Equivalent Fraction For 7 9
Sep 09, 2025
Related Post
Thank you for visiting our website which covers about Square Root Of 10 000 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.