Square Root Of 125 Cubed
saludintensiva
Sep 18, 2025 · 5 min read
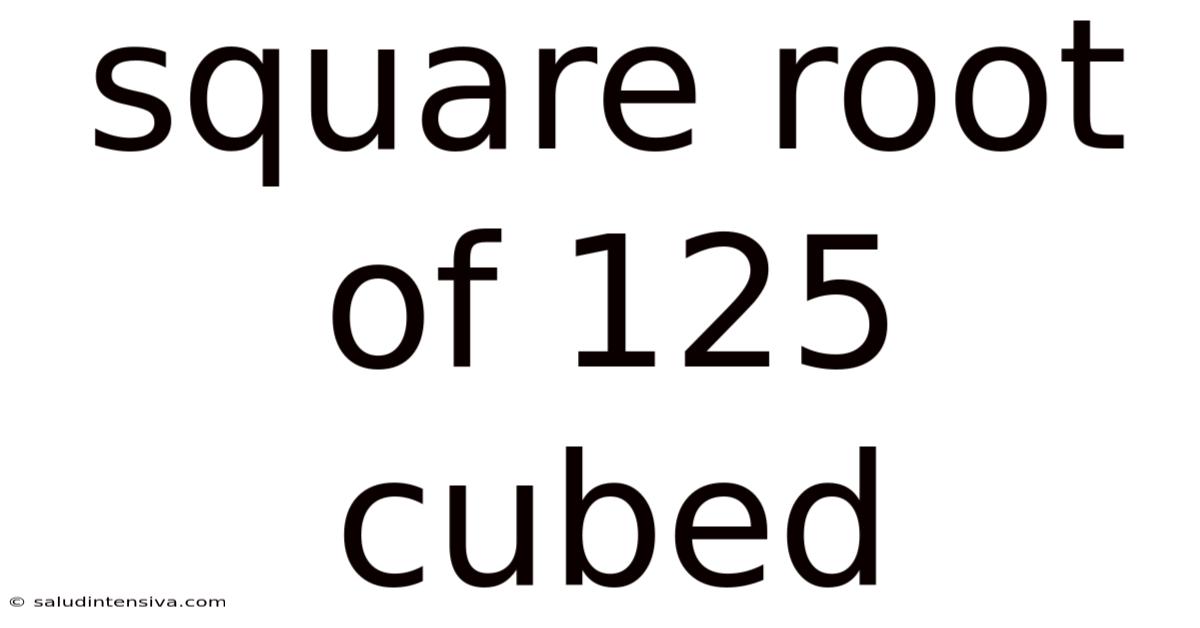
Table of Contents
Decoding the Mystery: Understanding the Cube of the Square Root of 125
Finding the cube of the square root of 125 might seem daunting at first glance, especially if you're not entirely comfortable with mathematical operations involving roots and exponents. But fear not! This seemingly complex problem can be broken down into manageable steps, revealing a surprisingly straightforward solution. This article will guide you through the process, explaining the underlying mathematical principles and providing a clear, step-by-step approach. By the end, you'll not only understand how to solve this specific problem but also develop a stronger grasp of square roots, cubes, and the order of operations.
Understanding the Problem: Square Root and Cube
Before diving into the solution, let's clarify the terminology. The problem asks us to find the cube of the square root of 125. Let's break that down:
-
Square root: The square root of a number is a value that, when multiplied by itself, gives the original number. For example, the square root of 9 is 3 (because 3 x 3 = 9). We often denote the square root using the symbol √.
-
Cube: The cube of a number is the result of multiplying that number by itself three times. For example, the cube of 2 is 8 (because 2 x 2 x 2 = 8). We can also represent this using an exponent: 2³.
Therefore, the problem "the cube of the square root of 125" can be mathematically expressed as: (√125)³
Step-by-Step Solution: Calculating (√125)³
Now, let's tackle the problem step-by-step:
Step 1: Find the square root of 125.
Finding the square root of 125 isn't as straightforward as finding the square root of a perfect square like 9 or 16. 125 isn't a perfect square; there's no whole number that, when multiplied by itself, equals 125. However, we can simplify it. We look for perfect square factors within 125. Notice that 125 = 25 x 5, and 25 is a perfect square (5 x 5 = 25). Therefore:
√125 = √(25 x 5) = √25 x √5 = 5√5
Step 2: Cube the result from Step 1.
Now that we've simplified the square root of 125 to 5√5, we need to cube this result. Remember, cubing means raising to the power of 3:
(5√5)³ = 5³ x (√5)³ = 125 x (√5)³
To cube √5, we can rewrite it as 5^(1/2). Then cubing it becomes: (5^(1/2))³ = 5^(3/2) = 5 * 5^(1/2) = 5√5
Therefore:
125 x (√5)³ = 125 x 5√5 = 625√5
Therefore, the cube of the square root of 125 is 625√5. This is the exact answer. If you need a decimal approximation, you can use a calculator to find the approximate value of √5 (approximately 2.236) and multiply it by 625.
Understanding the Underlying Mathematical Principles
This problem elegantly illustrates several important mathematical concepts:
-
Prime Factorization: Breaking down a number into its prime factors (numbers divisible only by 1 and themselves) is a fundamental technique in simplifying square roots and other mathematical operations. We used this when we factored 125 into 25 x 5.
-
Exponent Rules: Understanding how exponents work, especially the rules for multiplying and raising powers to powers, is crucial. We used the rule (a x b)ⁿ = aⁿ x bⁿ when cubing 5√5. We also applied the rule (a<sup>m</sup>)<sup>n</sup> = a<sup>mn</sup> when cubing 5<sup>1/2</sup>
-
Radical Simplification: Simplifying radicals (expressions involving square roots, cube roots, etc.) often involves finding perfect square (or cube, or higher power) factors and extracting them from the radical.
Further Exploration: Generalizing the Process
The method we used can be applied to similar problems involving different numbers. Let's consider a more general case: finding the cube of the square root of any number 'x'. This can be expressed as (√x)³. Following the same steps:
-
Find the square root of x: √x
-
Cube the result: (√x)³ = x√x
This shows that the cube of the square root of any number 'x' is always x√x. This provides a powerful shortcut for solving similar problems.
Frequently Asked Questions (FAQ)
Q1: Can I use a calculator to solve this directly?
A1: Yes, but it's beneficial to understand the steps involved. While a calculator can directly compute (√125)³, understanding the simplification process provides a deeper understanding of the mathematical concepts at play.
Q2: What if the problem asked for the square of the cube root of 125?
A2: That would be a different problem! It would be expressed as (∛125)² The cube root of 125 is 5 (since 5 x 5 x 5 = 125), and the square of 5 is 25.
Q3: Are there any other ways to solve (√125)³?
A3: Yes, you could express 125 as 5³, and then work with the exponents: (√5³)³ = (5^(3/2))³ = 5^(9/2) = 5^4 * 5^(1/2) = 625√5
Conclusion: Mastering Mathematical Operations
Solving the problem of finding the cube of the square root of 125 has provided us with a valuable opportunity to reinforce our understanding of square roots, cubes, and the order of operations. By breaking down the problem into smaller, manageable steps and understanding the underlying mathematical principles, we arrived at the exact answer: 625√5. Remember, mastering mathematical concepts like these is a process of building upon fundamental building blocks. Don't hesitate to revisit these steps and explore similar problems to solidify your understanding. The more you practice, the more confident and proficient you'll become in tackling even more complex mathematical challenges.
Latest Posts
Latest Posts
-
What Is This Number Pronounces
Sep 18, 2025
-
Greatest Common Factor Of 100
Sep 18, 2025
-
1 2 As An Improper Fraction
Sep 18, 2025
-
8 64 As A Fraction
Sep 18, 2025
-
2 To The Fourth Power
Sep 18, 2025
Related Post
Thank you for visiting our website which covers about Square Root Of 125 Cubed . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.