Square Root Of 28 Simplified
saludintensiva
Sep 22, 2025 · 5 min read
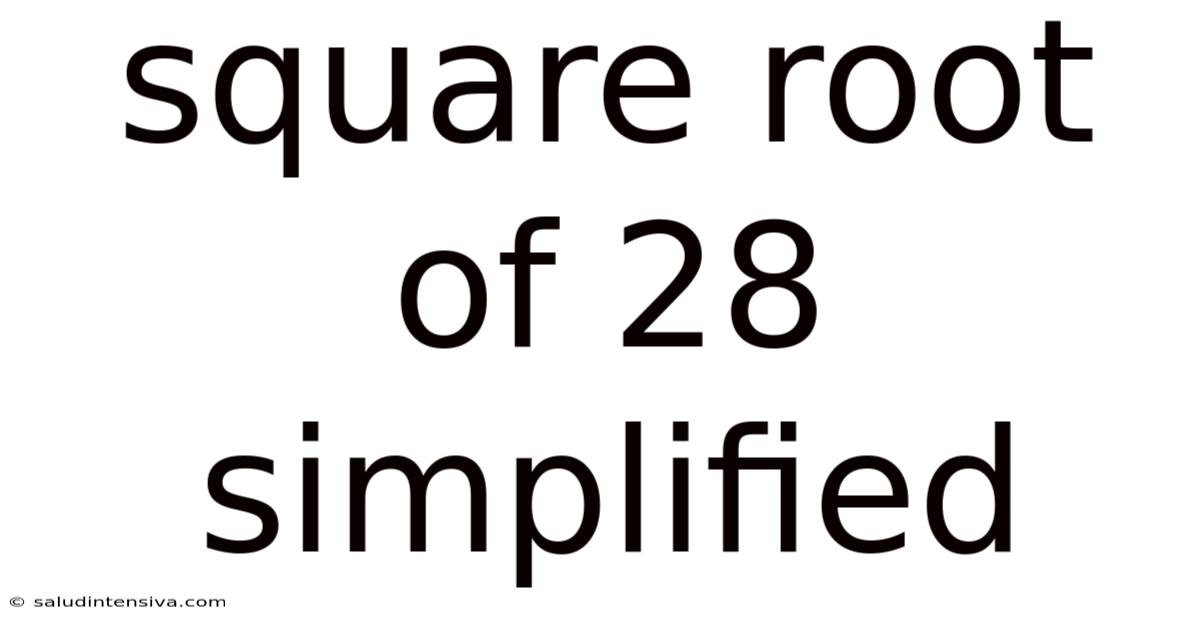
Table of Contents
Unveiling the Mysteries: Simplifying the Square Root of 28
The square root of 28, denoted as √28, might seem like a simple mathematical expression, but understanding its simplification reveals deeper insights into number theory and algebraic manipulation. This comprehensive guide will not only show you how to simplify √28 but also why the process works, equipping you with a solid understanding of square root simplification and its applications. We'll explore the concept step-by-step, incorporating examples and addressing frequently asked questions to ensure a clear and complete understanding.
Introduction: Understanding Square Roots
Before diving into the simplification of √28, let's establish a firm grasp on the fundamental concept of square roots. A square root of a number x is a value that, when multiplied by itself, equals x. For example, the square root of 9 (√9) is 3 because 3 multiplied by itself (3 x 3 = 9) equals 9. However, not all numbers have perfect square roots (i.e., whole number solutions). This is where simplification comes into play. Simplifying a square root involves expressing it in its simplest radical form, which means removing any perfect square factors from within the radical.
Step-by-Step Simplification of √28
The key to simplifying √28 lies in finding its prime factorization. Prime factorization is the process of breaking down a number into its prime factors (numbers divisible only by 1 and themselves). Let's break down 28:
-
Find the prime factorization of 28: 28 can be factored as 2 x 14. Further breaking down 14, we get 2 x 7. Therefore, the prime factorization of 28 is 2 x 2 x 7.
-
Rewrite the square root using the prime factorization: Now, we can rewrite √28 as √(2 x 2 x 7).
-
Identify perfect squares: Notice that we have a pair of 2s within the radical. A pair of identical factors represents a perfect square (2 x 2 = 2² = 4).
-
Simplify the square root: We can rewrite the expression as √(2² x 7). Since √(2²) = 2, we can simplify this to 2√7.
Therefore, the simplified form of √28 is 2√7.
Illustrative Examples: Expanding the Concept
Let's solidify our understanding with a few more examples. Simplifying square roots follows the same fundamental principle: prime factorization and identification of perfect squares.
-
Example 1: Simplifying √72:
- Prime factorization of 72: 2 x 2 x 2 x 3 x 3 = 2³ x 3²
- Rewrite the square root: √(2³ x 3²)
- Identify perfect squares: We have 2² and 3².
- Simplify: √(2² x 2 x 3²) = 2 x 3√2 = 6√2
Therefore, √72 simplifies to 6√2.
-
Example 2: Simplifying √128:
- Prime factorization of 128: 2 x 2 x 2 x 2 x 2 x 2 x 2 = 2⁷
- Rewrite the square root: √(2⁷)
- Identify perfect squares: We have multiple pairs of 2s. We can rewrite this as √(2² x 2² x 2² x 2)
- Simplify: 2 x 2 x 2√2 = 8√2
Therefore, √128 simplifies to 8√2.
-
Example 3: Simplifying √108:
- Prime factorization of 108: 2 x 2 x 3 x 3 x 3 = 2² x 3³
- Rewrite the square root: √(2² x 3³). We can rewrite 3³ as 3² x 3
- Identify perfect squares: We have 2² and 3².
- Simplify: √(2² x 3² x 3) = 2 x 3√3 = 6√3
Therefore, √108 simplifies to 6√3.
The Science Behind the Simplification: A Deeper Dive
The simplification process leverages fundamental properties of square roots and exponents. The key is understanding that √(a x b) = √a x √b, provided a and b are non-negative. This allows us to break down a complex square root into simpler ones. By identifying and extracting perfect square factors, we effectively remove them from under the radical sign, resulting in a simplified expression. This is closely related to the concept of exponent rules, specifically that √a = a^(1/2). Therefore, simplifying a square root involves manipulating exponents to express the number in its simplest radical form.
Frequently Asked Questions (FAQ)
-
Q: Why is it important to simplify square roots?
A: Simplifying square roots makes it easier to work with them in algebraic expressions and calculations. It leads to more concise and manageable expressions. Furthermore, it ensures the most accurate and efficient representation of a given number.
-
Q: What if I have a negative number under the square root?
A: The square root of a negative number involves imaginary numbers, denoted by i, where i² = -1. The simplification process is similar, but the final result will include i. For example, √-28 = √(-1 x 28) = √(-1) x √28 = i x 2√7 = 2i√7
-
Q: Can I simplify square roots with variables?
A: Yes, the same principles apply when simplifying square roots with variables. For example, simplifying √(x²y⁴) is possible by identifying that x² and y⁴ are perfect squares. This simplifies to x y²
-
Q: Are there any shortcuts to simplify square roots quickly?
A: While prime factorization is the most reliable method, practice and familiarity with perfect squares can help you identify common factors more readily, leading to faster simplification. Knowing common squares like 4, 9, 16, 25, 36, 49, 64, 81, 100, and so on, will help you in speeding up the simplification process.
Conclusion: Mastering Square Root Simplification
Mastering the art of simplifying square roots is a crucial skill in mathematics. This comprehensive guide has walked you through the process step-by-step, illustrating the underlying principles and addressing common questions. By understanding prime factorization, identifying perfect squares, and applying the relevant properties of square roots and exponents, you can confidently simplify any square root expression, whether it involves simple numbers or more complex expressions with variables. Remember, practice is key! The more you work through examples, the more comfortable and efficient you’ll become. With enough practice, simplifying square roots will become second nature. The journey to mastering this essential mathematical skill is achievable through consistent effort and attention to detail.
Latest Posts
Latest Posts
-
32 Inch Tv Dimensions In Cm
Sep 22, 2025
-
How Long Is 45 Days
Sep 22, 2025
-
6 X What Equals 48
Sep 22, 2025
-
Dividing Decimals By Decimals Problems
Sep 22, 2025
-
Lcm Of 50 And 75
Sep 22, 2025
Related Post
Thank you for visiting our website which covers about Square Root Of 28 Simplified . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.