Square Root Of 5 8
saludintensiva
Sep 22, 2025 · 5 min read
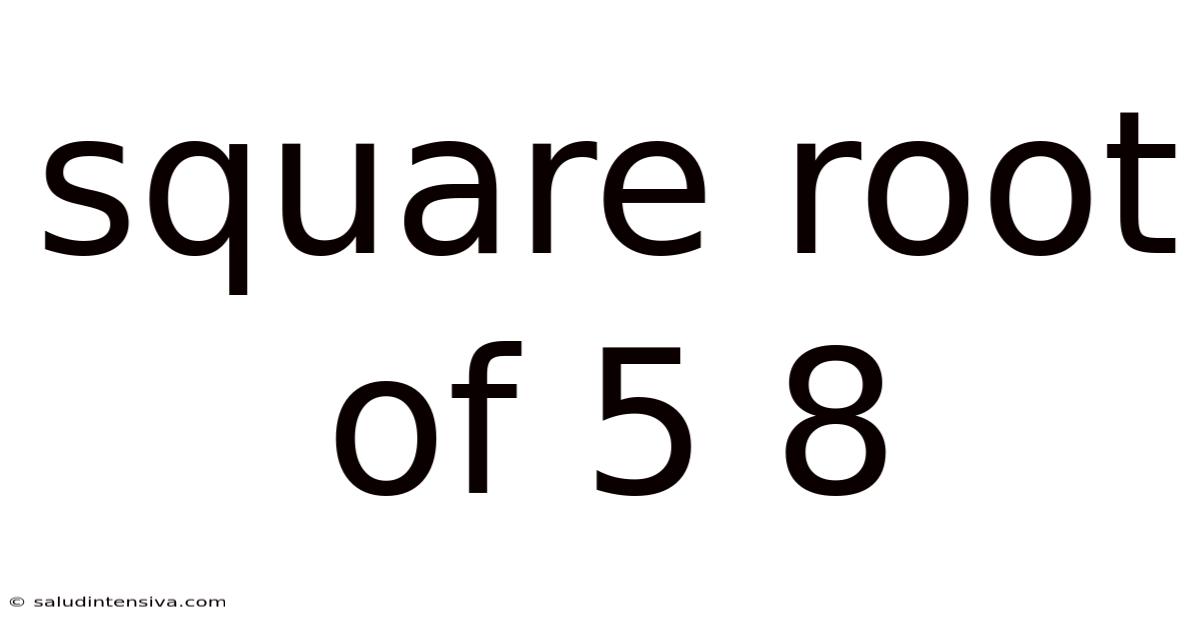
Table of Contents
Delving Deep into the Square Root of 58: A Comprehensive Exploration
The square root of 58, denoted as √58, is an irrational number, meaning it cannot be expressed as a simple fraction. This seemingly simple concept opens a door to a fascinating exploration of number theory, approximation techniques, and the beauty of mathematics hidden within seemingly mundane calculations. This article will delve deep into the square root of 58, exploring its properties, methods of approximation, and its relevance in various mathematical contexts. We will move beyond simply stating its approximate value and uncover the underlying mathematical principles.
Understanding the Concept: What is a Square Root?
Before we dive into the specifics of √58, let's solidify our understanding of square roots. The square root of a number x is a value y such that y multiplied by itself (y * y, or y²) equals x. In simpler terms, it's the number that, when squared, gives you the original number. For example, the square root of 9 (√9) is 3, because 3 * 3 = 9.
However, not all numbers have whole number square roots. Numbers like 58 are not perfect squares – they cannot be obtained by squaring a whole number. This is where the concept of irrational numbers comes into play. Irrational numbers have decimal representations that neither terminate nor repeat.
Approximating √58: Methods and Techniques
Since √58 is irrational, we cannot express it exactly as a decimal. However, we can approximate its value using various methods.
1. Using a Calculator: The Easiest Approach
The simplest way to find an approximate value for √58 is to use a calculator. Most calculators have a square root function (√). Inputting 58 and pressing the square root button will yield an approximation, typically to several decimal places. A calculator will usually show something like 7.6157731...
While convenient, this method doesn't offer insight into how the approximation is obtained. Let's explore more insightful techniques.
2. The Babylonian Method (or Heron's Method): An Iterative Approach
The Babylonian method is an ancient algorithm for approximating square roots. It's an iterative method, meaning it refines the approximation through repeated steps. The steps are as follows:
-
Make an initial guess: Start with a reasonable guess for √58. Since 7² = 49 and 8² = 64, a good initial guess would be 7.5.
-
Improve the guess: Divide 58 by your initial guess (58 / 7.5 ≈ 7.733).
-
Average the results: Average the result from step 2 with your initial guess: (7.5 + 7.733) / 2 ≈ 7.6165.
-
Repeat: Use the result from step 3 as your new guess and repeat steps 2 and 3 until the desired level of accuracy is achieved.
Let's perform a few iterations:
- Iteration 1: Guess = 7.5; 58 / 7.5 ≈ 7.733; Average ≈ 7.6165
- Iteration 2: Guess = 7.6165; 58 / 7.6165 ≈ 7.6157; Average ≈ 7.6161
As you can see, the approximation quickly converges to the actual value. The more iterations you perform, the closer your approximation gets to the true value of √58.
3. Using Linear Approximation: A Simpler Method
For a less computationally intensive method, linear approximation can be used. This method leverages the tangent line of a function at a known point. Consider the function f(x) = √x. We know that √49 = 7 and √64 = 8. Since 58 lies between 49 and 64, we can use linear interpolation.
The slope of the tangent line near x = 49 is approximately 1/(2√49) = 1/14. Therefore, we can approximate:
√58 ≈ 7 + (58 - 49) * (1/14) ≈ 7 + 9/14 ≈ 7.64
This method is less precise than the Babylonian method but provides a quick estimate.
The Importance of Irrational Numbers: Beyond the Square Root
The irrationality of √58 highlights a crucial aspect of mathematics: the existence of numbers that cannot be expressed as simple fractions. Irrational numbers are fundamental to many areas of mathematics and science:
-
Geometry: The diagonal of a square with side length 1 is √2, an irrational number. Irrational numbers frequently appear in geometric calculations involving angles and lengths.
-
Trigonometry: Trigonometric functions like sine, cosine, and tangent often produce irrational values for certain angles.
-
Calculus: Many important mathematical constants, such as π (pi) and e (Euler's number), are irrational numbers. These are crucial in calculus and its applications.
-
Physics: Irrational numbers frequently appear in physics equations, describing phenomena such as wave oscillations and orbital mechanics.
Exploring √58 in Different Number Systems
While we typically work with the decimal representation of √58, it's worthwhile to consider its representation in other number systems:
-
Continued Fraction: √58 can be represented as a continued fraction: 7 + 1/(1 + 1/(1 + 1/(1 + 1/(14 + ...)))). This representation offers a unique way to express the number and provides insights into its properties.
-
Binary Representation: Just as numbers have decimal representations, they also have binary (base-2) representations. The binary representation of √58 would be a non-terminating sequence of 0s and 1s.
Frequently Asked Questions (FAQs)
Q: Is √58 a rational or irrational number?
A: √58 is an irrational number. It cannot be expressed as a fraction of two integers.
Q: What is the best way to approximate √58?
A: The Babylonian method offers a highly accurate and efficient way to approximate √58. Calculators provide the most convenient but least insightful approach.
Q: Are there other irrational numbers similar to √58?
A: Yes, there are infinitely many other irrational numbers. Most square roots of non-perfect squares are irrational.
Q: What is the significance of irrational numbers in mathematics?
A: Irrational numbers are fundamental to many areas of mathematics and science, appearing in various equations and calculations related to geometry, trigonometry, calculus, and physics.
Conclusion: The Enduring Mystery of √58
The square root of 58, while seemingly a simple concept, unveils a wealth of mathematical richness. Its irrationality underscores the complexity and beauty of the number system. Understanding its approximation methods, exploring its representation in different systems, and recognizing its relevance in wider mathematical and scientific contexts enrich our appreciation for the subtle wonders of mathematics. This exploration is not just about finding a numerical approximation; it's about understanding the underlying principles and appreciating the elegant intricacies of the mathematical world. The journey to understanding √58, and indeed all irrational numbers, is a continuous one, filled with fascinating discoveries and intellectual challenges.
Latest Posts
Latest Posts
-
115 Deg F To C
Sep 22, 2025
-
18 30 In Standard Time
Sep 22, 2025
-
How To Add Subtract Radicals
Sep 22, 2025
-
Gcf Of 77 And 56
Sep 22, 2025
-
57 Degrees Fahrenheit In Celsius
Sep 22, 2025
Related Post
Thank you for visiting our website which covers about Square Root Of 5 8 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.