Square Root Of Negative 81
saludintensiva
Sep 15, 2025 · 5 min read
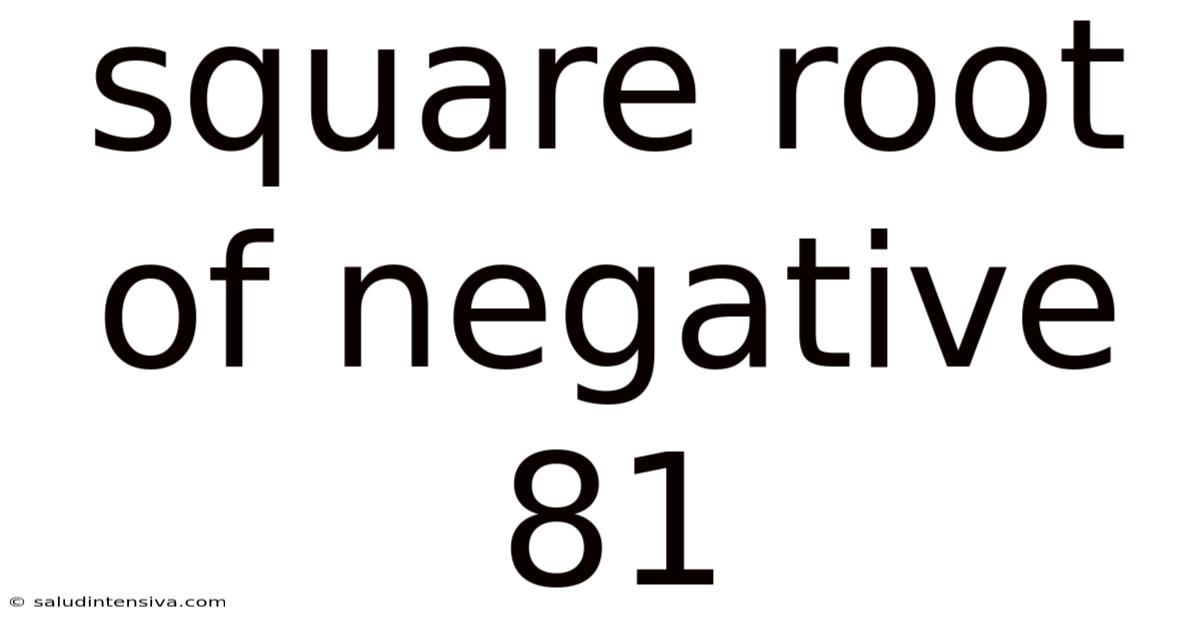
Table of Contents
Delving into the Depths: Understanding the Square Root of Negative 81
The square root of -81 might seem like a simple mathematical problem at first glance. After all, we all know that the square root of 81 is 9, right? But introducing a negative sign into the mix opens up a whole new world of mathematical concepts, leading us into the fascinating realm of imaginary numbers and complex numbers. This article will explore the square root of -81, explaining its solution, the underlying principles, and its applications in various fields. We'll unravel the mystery step-by-step, ensuring a comprehensive understanding even for those with a limited background in advanced mathematics.
Understanding Square Roots and Negative Numbers
Before diving into the complexities of the square root of -81, let's refresh our understanding of basic mathematical concepts. A square root of a number is a value that, when multiplied by itself, equals the original number. For example, the square root of 9 (√9) is 3 because 3 x 3 = 9. Similarly, the square root of 16 (√16) is 4 because 4 x 4 = 16.
Now, let's introduce negative numbers. The square root of a positive number is always positive. However, we run into a problem when dealing with the square root of a negative number. There's no real number that, when multiplied by itself, results in a negative number. This is because a positive number multiplied by a positive number is always positive, and a negative number multiplied by a negative number is also always positive.
This apparent impossibility led mathematicians to define a new type of number: the imaginary number.
Introducing the Imaginary Unit: 'i'
The imaginary unit, denoted by the letter i, is defined as the square root of -1: i = √-1. This might seem arbitrary, but it's a fundamental building block for expanding our understanding of numbers beyond the real number system.
Now, armed with the imaginary unit, we can tackle the square root of -81.
Calculating the Square Root of -81
We can express √-81 using the properties of square roots and the imaginary unit:
√-81 = √(81 x -1) = √81 x √-1
Since √81 = 9 and √-1 = i, we can substitute these values:
√-81 = 9*i
Therefore, the square root of -81 is 9i. This is an imaginary number.
Complex Numbers: Combining Real and Imaginary
While 9i is a perfectly valid solution, it's important to note that it's not a real number. Instead, it's an imaginary number. The combination of real and imaginary numbers forms a broader set known as complex numbers. A complex number is written in the form a + bi, where a is the real part and b is the imaginary part. In the case of √-81, a = 0 and b = 9, giving us the complex number 0 + 9i, or simply 9i.
Visualizing Complex Numbers: The Complex Plane
Unlike real numbers, which can be represented on a single number line, complex numbers require a two-dimensional representation called the complex plane. The horizontal axis represents the real part (a), and the vertical axis represents the imaginary part (b). The complex number 9i would be plotted on the vertical axis, 9 units above the origin.
Applications of Imaginary and Complex Numbers
While they might seem abstract, imaginary and complex numbers have numerous practical applications in various fields:
-
Electrical Engineering: Complex numbers are crucial in analyzing alternating current (AC) circuits. They simplify calculations involving impedance, voltage, and current.
-
Quantum Mechanics: Imaginary numbers play a fundamental role in quantum mechanics, where wave functions and probabilities are often expressed using complex numbers.
-
Signal Processing: Complex numbers are essential for representing and manipulating signals in various applications, including audio processing and image processing.
-
Fluid Dynamics: Complex analysis is used in solving certain types of fluid flow problems.
-
Fractals: Many beautiful and complex fractals are generated using iterative processes that involve complex numbers. The Mandelbrot set is a prime example.
Frequently Asked Questions (FAQ)
Q: Is the square root of -81 a real number?
A: No, the square root of -81 is not a real number. It's an imaginary number, specifically 9i.
Q: What is the difference between a real number and an imaginary number?
A: Real numbers are numbers that can be plotted on a number line (e.g., 1, -2, 0, π). Imaginary numbers are multiples of the imaginary unit i (√-1).
Q: Can I have a negative square root?
A: The principal square root of a positive number is always positive. However, every positive number has two square roots: a positive one and a negative one. For example, the square roots of 9 are +3 and -3. In the case of negative numbers, the square roots are imaginary numbers. The square roots of -81 are +9i and -9i.
Q: What is a complex number?
A: A complex number is a number of the form a + bi, where a and b are real numbers and i is the imaginary unit. a is the real part, and b is the imaginary part.
Q: Why are imaginary numbers important?
A: Imaginary numbers, while seemingly abstract, are essential for solving many real-world problems in fields like electrical engineering, quantum mechanics, and signal processing. They provide a framework for solving equations that cannot be solved using only real numbers.
Conclusion: Expanding Mathematical Horizons
The square root of -81, which is 9i, might initially appear perplexing. However, by understanding the concept of imaginary numbers and their place within the broader framework of complex numbers, we can appreciate their significance and applicability. This seemingly simple problem serves as a gateway to a deeper understanding of mathematics and its power to unravel complex phenomena across various scientific and engineering disciplines. The journey into the world of complex numbers offers a fascinating exploration of mathematical concepts that extend far beyond the realm of simple arithmetic, opening doors to a richer and more nuanced understanding of the universe around us.
Latest Posts
Latest Posts
-
Gcf Of 25 And 30
Sep 15, 2025
-
Lcm Of 8 4 6
Sep 15, 2025
-
4 2 3 3 4
Sep 15, 2025
-
Gcf Of 20 And 10
Sep 15, 2025
-
Can There Be No Mode
Sep 15, 2025
Related Post
Thank you for visiting our website which covers about Square Root Of Negative 81 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.