The Cube Root Of 27
saludintensiva
Sep 17, 2025 · 6 min read
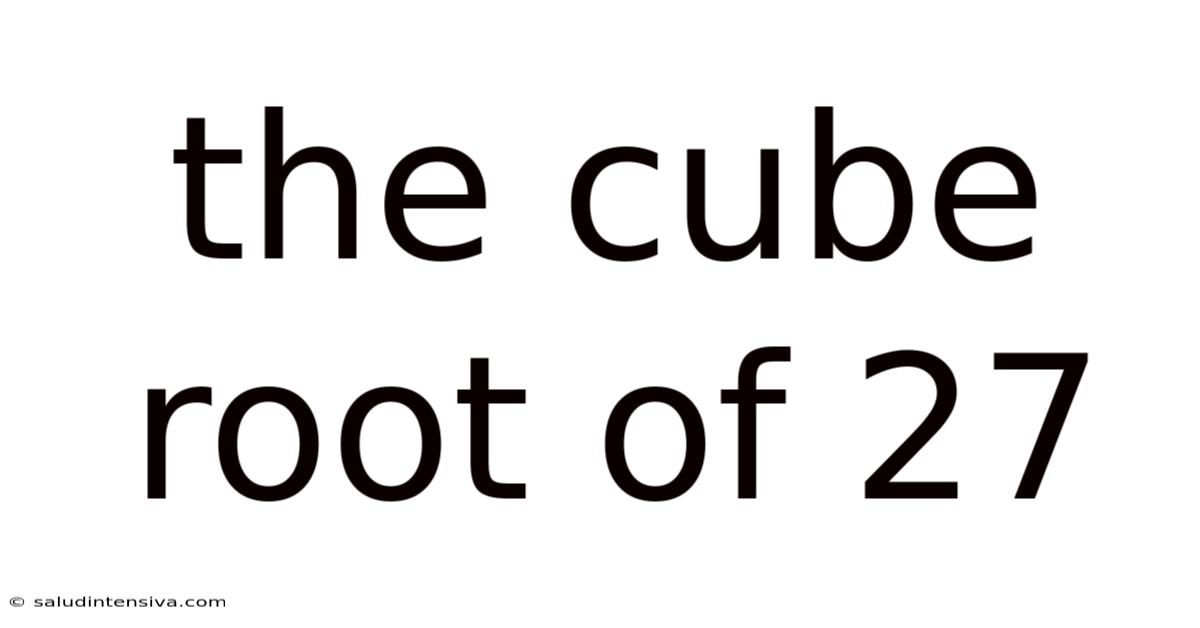
Table of Contents
Unveiling the Mysteries of the Cube Root of 27: A Deep Dive into Cubic Functions and their Applications
Finding the cube root of 27 might seem like a simple mathematical exercise, something easily tackled with a calculator. But beneath this seemingly straightforward calculation lies a rich tapestry of mathematical concepts, practical applications, and historical context that deserve exploration. This article will delve into the meaning of cube roots, explore different methods for calculating the cube root of 27, discuss its significance within the broader context of cubic functions and equations, and examine its real-world applications. Understanding the cube root of 27 is not just about getting the answer; it's about grasping the fundamental principles of mathematics and appreciating its power in solving real-world problems.
Understanding Cube Roots: A Fundamental Concept
Before we dive into the specifics of the cube root of 27, let's establish a solid understanding of what a cube root actually is. In mathematics, the cube root of a number is a value that, when multiplied by itself three times (cubed), results in the original number. This is represented mathematically as:
∛x = y if and only if y³ = x
In simpler terms, if you have a cube with a volume of 'x', the cube root of 'x' (∛x) will tell you the length of one side of that cube.
For example:
- ∛8 = 2 because 2 × 2 × 2 = 8
- ∛64 = 4 because 4 × 4 × 4 = 64
- ∛125 = 5 because 5 × 5 × 5 = 125
Calculating the Cube Root of 27: Multiple Approaches
There are several ways to calculate the cube root of 27. Let's explore a few:
1. Memorization and Basic Arithmetic:
For smaller numbers like 27, memorization can be efficient. If you know your cubes up to 10 (1³=1, 2³=8, 3³=27, 4³=64, 5³=125, and so on), you'll instantly recognize that the cube root of 27 is 3. This is because 3 × 3 × 3 = 27.
2. Using a Calculator:
The most straightforward method is using a calculator. Most scientific calculators have a dedicated cube root function (often denoted as ³√ or x^(1/3)). Simply enter 27 and press the cube root button to get the answer, 3.
3. Prime Factorization:
This method is particularly useful for larger numbers. We break down the number into its prime factors. For 27:
27 = 3 × 3 × 3 = 3³
Since 27 is expressed as 3 cubed, its cube root is 3.
4. Numerical Methods (for larger, non-perfect cubes):
For numbers that aren't perfect cubes, numerical methods like the Newton-Raphson method are used to approximate the cube root. These iterative methods refine an initial guess until the desired accuracy is achieved. While not necessary for 27, understanding these methods provides valuable insight into how cube roots are calculated for more complex numbers.
The Cube Root of 27 in the Context of Cubic Functions and Equations
The cube root of 27 is intimately connected to the concept of cubic functions and equations. A cubic function is a polynomial function of the third degree, generally represented as:
f(x) = ax³ + bx² + cx + d
where 'a', 'b', 'c', and 'd' are constants, and 'a' is not equal to zero. Solving a cubic equation (finding the values of 'x' that make f(x) = 0) can involve finding cube roots.
Consider a simple cubic equation:
x³ - 27 = 0
This can be rewritten as:
x³ = 27
Solving for 'x' requires finding the cube root of 27, which, as we've established, is 3. Therefore, x = 3 is a solution to this cubic equation. Note that cubic equations can have up to three real roots, though in this case there is only one real root (3). The other two roots are complex numbers.
Real-World Applications: Where Cube Roots Matter
The concept of cube roots, though seemingly abstract, has several practical applications across various fields:
1. Volume and Geometry:
As mentioned earlier, cube roots are fundamental in calculating the side length of a cube given its volume. This has implications in various fields, including:
- Engineering: Determining the dimensions of cubic containers, structural elements, or components.
- Architecture: Designing cubic structures, spaces, or rooms.
- Packaging: Designing cubic boxes or containers for products.
2. Physics and Chemistry:
Cube roots appear in various physical and chemical formulas:
- Calculating the radius of a sphere given its volume: The formula involves a cube root.
- Certain thermodynamic calculations: Cube roots are involved in determining specific properties of substances.
- Fluid dynamics: Analyzing the flow of fluids through pipes often involves cubic relationships.
3. Statistics:
Cube roots can be used in statistical calculations, particularly when dealing with data exhibiting cubic relationships.
Frequently Asked Questions (FAQ)
Q: Is there only one cube root for a given number?
A: For every positive real number, there is only one real cube root. However, in the complex number system, every nonzero number has three cube roots. For example, the cube roots of 27 are 3, -1.5 + 2.598i, and -1.5 - 2.598i (where 'i' is the imaginary unit).
Q: How can I calculate the cube root of a negative number?
A: The cube root of a negative number is simply the negative of the cube root of its absolute value. For example, ∛(-27) = -3 because (-3) × (-3) × (-3) = -27.
Q: Are there any online tools or software for calculating cube roots?
A: Yes, many online calculators and mathematical software packages (like Wolfram Alpha, MATLAB, or Python's NumPy library) offer functions to calculate cube roots, as well as more advanced mathematical operations.
Q: How do cube roots relate to other mathematical concepts?
A: Cube roots are closely linked to other mathematical concepts such as exponents, powers, polynomials, and equations. They play a significant role in solving cubic equations and understanding the behavior of cubic functions. Furthermore, they are connected to more advanced mathematical fields such as complex analysis.
Conclusion: Beyond the Simple Answer
While the cube root of 27 is simply 3, the journey to understanding this seemingly basic calculation has opened doors to a wealth of mathematical knowledge. From the fundamental definition of cube roots to their practical applications across numerous disciplines, this exploration has highlighted the depth and interconnectedness of mathematical concepts. The next time you encounter a cube root, remember that it's not just a number; it's a gateway to a deeper understanding of the world around us. This seemingly simple calculation is a testament to the elegance and power of mathematics, offering insights far beyond its immediate answer. The understanding of cube roots, and their applications, extends beyond simply solving equations and is crucial for various aspects of mathematics, science, engineering, and even finance. Therefore, the significance of understanding a seemingly simple concept like the cube root of 27 should not be underestimated.
Latest Posts
Latest Posts
-
Convert 240 Kg To Pounds
Sep 17, 2025
-
Gcf Of 42 And 35
Sep 17, 2025
-
21 Is 75 Of What
Sep 17, 2025
-
Gcf Of 3 And 8
Sep 17, 2025
-
90 Days From 10 23
Sep 17, 2025
Related Post
Thank you for visiting our website which covers about The Cube Root Of 27 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.