What 25 Percent Of 100
saludintensiva
Sep 18, 2025 · 5 min read
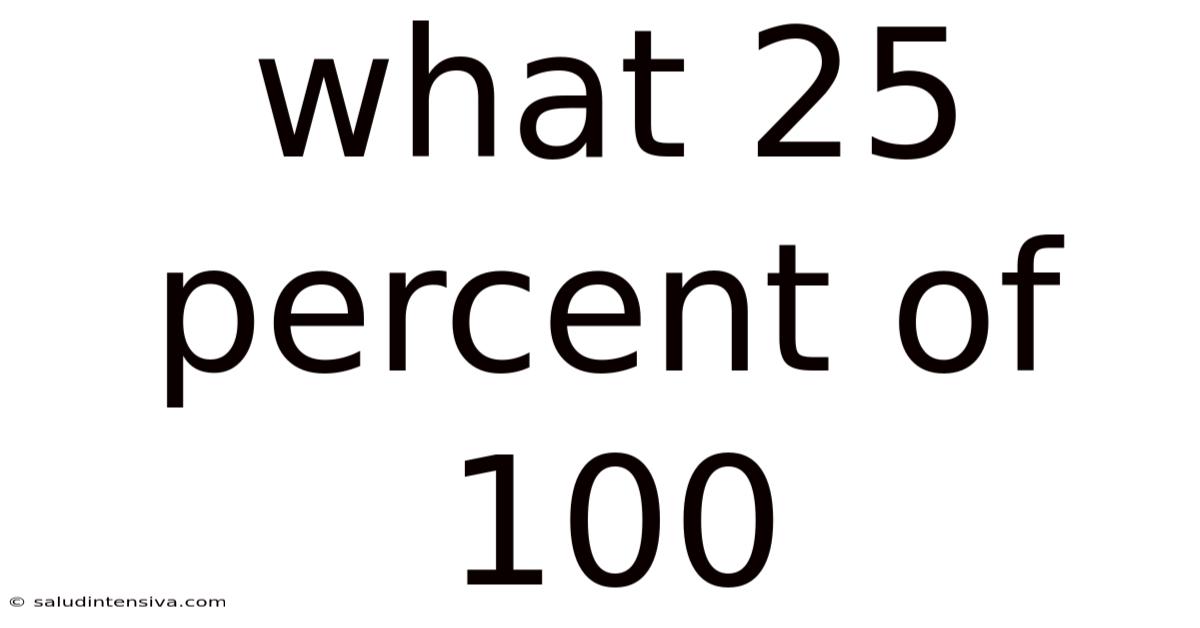
Table of Contents
What is 25 Percent of 100? A Deep Dive into Percentages and Their Applications
Finding 25 percent of 100 might seem like a simple calculation, easily solved with a quick mental calculation or a calculator. However, understanding the underlying principles of percentages is crucial for various applications in everyday life, from calculating discounts and taxes to understanding statistical data and financial reports. This article will delve into the calculation of 25% of 100, exploring different methods, explaining the underlying mathematical concepts, and highlighting practical applications of percentages in various fields.
Understanding Percentages: A Foundation
A percentage is a way of expressing a number as a fraction of 100. The word "percent" literally means "out of one hundred" ( per centum in Latin). Therefore, 25% can be understood as 25 parts out of 100 equal parts of a whole. This fractional representation is key to understanding percentage calculations. We can represent 25% as a fraction (25/100), a decimal (0.25), or, of course, as a percentage (25%).
Calculating 25% of 100: Three Approaches
There are several ways to calculate 25% of 100. Let's explore three common methods:
1. The Fraction Method:
This is perhaps the most intuitive approach, especially for understanding the core concept. We know that 25% is equivalent to the fraction 25/100. To find 25% of 100, we simply multiply the fraction by the number:
(25/100) * 100 = 25
This method clearly shows that 25 out of 100 parts of 100 is 25.
2. The Decimal Method:
Converting the percentage to a decimal simplifies the calculation. To convert 25% to a decimal, we divide it by 100:
25% / 100 = 0.25
Now, we multiply this decimal by 100:
0.25 * 100 = 25
This method is efficient and commonly used in calculators and computer programs.
3. The Mental Calculation Method:
For this specific problem (25% of 100), a mental calculation is easily performed. Since 25% is a quarter (1/4), we can directly calculate a quarter of 100:
100 / 4 = 25
This method leverages our understanding of fractions and is quick for simple percentages.
Beyond the Basics: Understanding Percentage Change
While finding 25% of 100 provides a fundamental understanding of percentages, it's essential to explore the concept of percentage change. This is frequently used to compare values over time or across different categories. Percentage change is calculated as:
[(New Value - Old Value) / Old Value] * 100%
For example, if a quantity increased from 80 to 100, the percentage increase would be:
[(100 - 80) / 80] * 100% = 25%
Conversely, if a quantity decreased from 100 to 75, the percentage decrease would be:
[(75 - 100) / 100] * 100% = -25%
Practical Applications of Percentages
The applications of percentages are vast and span numerous fields:
-
Finance: Calculating interest rates, discounts, taxes, profits, and losses. For instance, a 25% discount on a $100 item would result in a $25 discount, leaving a final price of $75. Understanding compound interest, which involves calculating interest on both the principal and accumulated interest, requires a strong grasp of percentages.
-
Retail: Pricing strategies, sales, and markups often involve percentage calculations. Retailers use percentages to determine profit margins and to offer discounts to customers.
-
Statistics: Percentages are essential for presenting and interpreting data. For example, survey results, election polls, and demographic information are often expressed using percentages to represent proportions within a population.
-
Science: Many scientific measurements and calculations utilize percentages. For example, expressing the concentration of a solution (e.g., 25% saline solution) or the efficiency of a process.
-
Everyday Life: Calculating tips in restaurants, understanding nutritional information on food labels, and comprehending sales tax all involve percentage calculations.
Solving More Complex Percentage Problems
While 25% of 100 is a straightforward calculation, let's explore a more challenging example: Finding x% of y.
The general formula for calculating x% of y is:
(x/100) * y = Result
For instance, to find 15% of 300:
(15/100) * 300 = 45
To find what percentage x is of y:
(x/y) * 100% = Percentage
Frequently Asked Questions (FAQs)
Q: What is the easiest way to calculate percentages?
A: The easiest method depends on the specific problem. For simple percentages like 25% of 100, mental calculation is often quickest. For more complex calculations, using a calculator or converting the percentage to a decimal is generally more efficient.
Q: How do I calculate percentage increase or decrease?
A: The formula for percentage change is [(New Value - Old Value) / Old Value] * 100%. A positive result indicates an increase, while a negative result indicates a decrease.
Q: Are there any online tools or calculators to help with percentage calculations?
A: Yes, many online calculators and tools are available to assist with percentage calculations. These tools can simplify complex calculations and ensure accuracy.
Q: Why are percentages important in everyday life?
A: Percentages are crucial for understanding and interpreting numerical information in various contexts, from personal finances to scientific data. They provide a standardized way to express proportions and make comparisons.
Conclusion: Mastering Percentages for Real-World Success
Understanding percentages is a fundamental skill with far-reaching applications. While calculating 25% of 100 is a simple starting point, grasping the underlying principles and exploring different calculation methods empowers you to tackle more complex problems across various domains. From managing your personal finances to interpreting statistical data, a solid understanding of percentages is invaluable in navigating the complexities of the modern world. By mastering these concepts, you equip yourself with a powerful tool for problem-solving and informed decision-making. The seemingly simple calculation of 25% of 100 serves as a gateway to a deeper understanding of a mathematical concept with widespread practical relevance.
Latest Posts
Latest Posts
-
3 5 3 Simplified As A Fraction
Sep 18, 2025
-
175 Degrees F To C
Sep 18, 2025
-
What Time Is 21 48
Sep 18, 2025
-
1 20 Number Generator
Sep 18, 2025
-
Time In A Half Calculator
Sep 18, 2025
Related Post
Thank you for visiting our website which covers about What 25 Percent Of 100 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.