What Does 3 Squared Equal
saludintensiva
Sep 11, 2025 · 6 min read
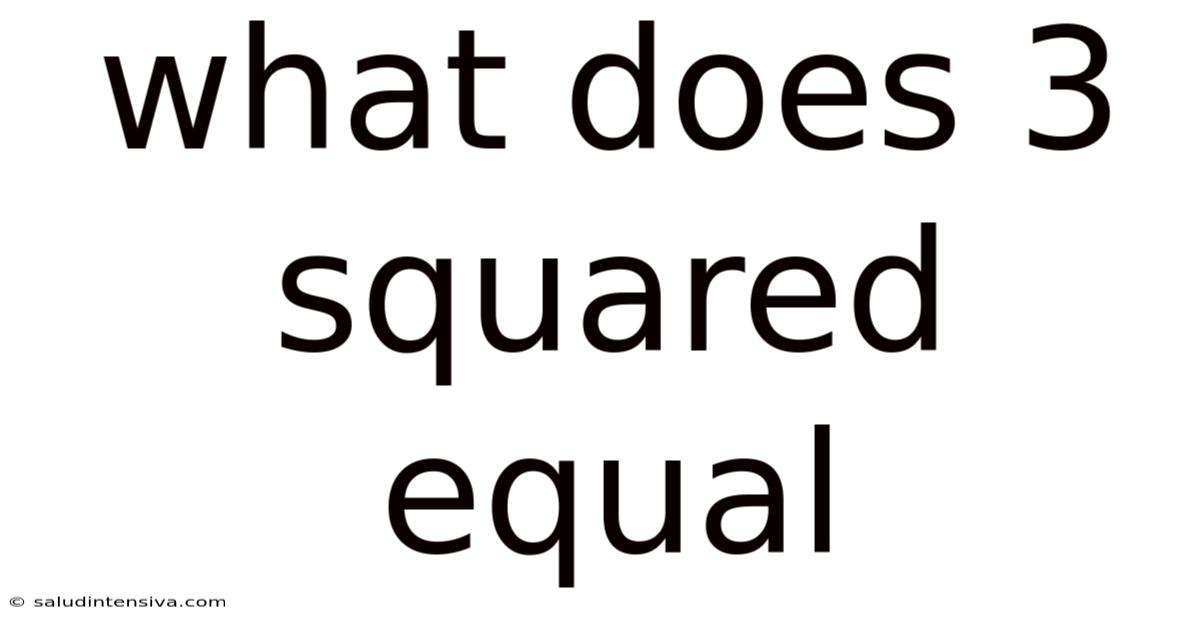
Table of Contents
What Does 3 Squared Equal? Unraveling the Power of Exponents
This article delves into the seemingly simple question: what does 3 squared equal? While the answer itself is straightforward (9), the underlying concept of squaring numbers—and exponents in general—holds significant mathematical importance and wide-ranging applications. We'll explore not just the answer but also the broader implications of exponents, their applications, and related mathematical concepts, ensuring a comprehensive understanding for all levels of mathematical proficiency.
Understanding Exponents: The Basics
Before diving into the specific case of 3 squared, let's establish a firm grasp of exponents. An exponent, also known as a power or index, indicates how many times a number (the base) is multiplied by itself. It's written as a superscript to the base. For instance, in the expression 3², the number 3 is the base, and the number 2 is the exponent. This is read as "3 raised to the power of 2" or "3 squared."
What does 3 squared (3²) mean? It simply means 3 multiplied by itself: 3 x 3 = 9. Therefore, 3 squared equals 9.
Beyond Squaring: Exploring Higher Powers
While squaring (raising to the power of 2) is common, exponents can be any whole number, including larger numbers. Let's look at some examples using the base 3:
- 3¹ (3 raised to the power of 1): This is simply 3. Any number raised to the power of 1 is itself.
- 3³ (3 cubed or 3 raised to the power of 3): This means 3 x 3 x 3 = 27. Cubing a number represents its volume in three-dimensional space.
- 3⁴ (3 raised to the power of 4): This is 3 x 3 x 3 x 3 = 81.
- 3⁵ (3 raised to the power of 5): This is 3 x 3 x 3 x 3 x 3 = 243. And so on.
The pattern is clear: the exponent tells us how many times the base is used as a factor in the multiplication.
Negative Exponents: Inverting the Base
Exponents aren't limited to positive whole numbers. Negative exponents introduce an interesting twist: they represent the reciprocal of the base raised to the positive power.
- 3⁻¹ (3 raised to the power of -1): This is equal to 1/3¹ = 1/3.
- 3⁻² (3 raised to the power of -2): This is equal to 1/3² = 1/9.
- 3⁻³ (3 raised to the power of -3): This is equal to 1/3³ = 1/27.
In essence, a negative exponent flips the base into the denominator of a fraction.
Zero Exponent: A Special Case
Another special case is the zero exponent. Any non-zero number raised to the power of 0 equals 1.
- 3⁰ (3 raised to the power of 0): This equals 1.
This might seem counterintuitive, but it's consistent with the pattern of exponents and maintains the rules of algebra.
Fractional Exponents: Introducing Roots
Fractional exponents introduce the concept of roots. For example:
- 3¹/² (3 raised to the power of 1/2): This is the same as the square root of 3 (√3). It's the number that, when multiplied by itself, equals 3.
- 3²/³ (3 raised to the power of 2/3): This is the same as the cube root of 3 squared (∛(3²)) or (∛9).
The numerator of the fraction represents the power, and the denominator represents the root.
Real-World Applications of Exponents
The concept of exponents extends far beyond abstract mathematics. They have numerous real-world applications, including:
- Compound Interest: Calculating compound interest involves exponents. The formula uses exponents to determine the future value of an investment based on the principal amount, interest rate, and time period.
- Population Growth: Exponents are essential in modeling population growth. Exponential growth is characterized by a constant percentage increase over time.
- Radioactive Decay: Radioactive decay follows an exponential decay model, where the amount of radioactive material decreases exponentially over time.
- Computer Science: Exponents are fundamental in computer science, particularly in algorithms and data structures. Binary numbers, which are the foundation of computer systems, utilize powers of 2.
- Physics: Many physical phenomena, such as the intensity of light or sound, are described by exponential relationships.
- Engineering: Exponents are used extensively in various engineering disciplines, including structural engineering, electrical engineering, and mechanical engineering, to model and analyze systems.
Solving Equations with Exponents
Understanding exponents is crucial for solving various algebraic equations. For instance, consider the equation:
x² = 9
To solve for x, we take the square root of both sides:
√x² = √9
x = ±3
This shows that there can be two solutions when dealing with even-numbered exponents.
Common Mistakes to Avoid
When working with exponents, several common mistakes can occur:
- Incorrect Order of Operations: Remember the order of operations (PEMDAS/BODMAS): Parentheses/Brackets, Exponents/Orders, Multiplication and Division (from left to right), Addition and Subtraction (from left to right).
- Confusing Exponents with Multiplication: 3² is not 3 x 2; it's 3 x 3.
- Incorrectly Handling Negative Exponents: Remember that a negative exponent doesn't make the base negative; it indicates a reciprocal.
Frequently Asked Questions (FAQ)
Q: What is the difference between 3² and 2³?
A: 3² (3 squared) is 3 x 3 = 9. 2³ (2 cubed) is 2 x 2 x 2 = 8. The base and exponent are different in each case, leading to different results.
Q: Can exponents be decimals or irrational numbers?
A: Yes, exponents can be any real number, including decimals and irrational numbers like π (pi). This expands the concept into more advanced areas of mathematics.
Q: How do I calculate 3 raised to a large power?
A: For large powers, calculators or computer software are generally used. These tools are efficient for handling complex calculations involving exponents.
Q: What are some practical applications of exponents in everyday life?
A: Many everyday phenomena involve exponential relationships, such as the growth of bacteria, the decay of medication in the body, and the spread of information on social media.
Conclusion: The Power of Understanding Exponents
While the answer to "What does 3 squared equal?" is a simple 9, understanding the concept of exponents unlocks a wealth of mathematical possibilities. From basic arithmetic to complex calculations in various scientific and engineering fields, exponents play a crucial role. Mastering exponents provides a strong foundation for further mathematical exploration and opens doors to understanding a wide range of phenomena in the world around us. The seemingly simple concept of squaring a number, like 3², acts as a gateway to a more profound understanding of the power of mathematics. It's a journey of exploration, revealing the elegance and utility of mathematical principles in diverse applications.
Latest Posts
Latest Posts
-
22 9 As A Mixed Number
Sep 12, 2025
-
1 88 Meters To Feet
Sep 12, 2025
-
4 10 In A Decimal
Sep 12, 2025
-
Convert 1 5 To A Fraction
Sep 12, 2025
-
90 Degrees Fahrenheit In Celsius
Sep 12, 2025
Related Post
Thank you for visiting our website which covers about What Does 3 Squared Equal . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.