What Is 1/2 - 1/5
saludintensiva
Sep 19, 2025 · 6 min read
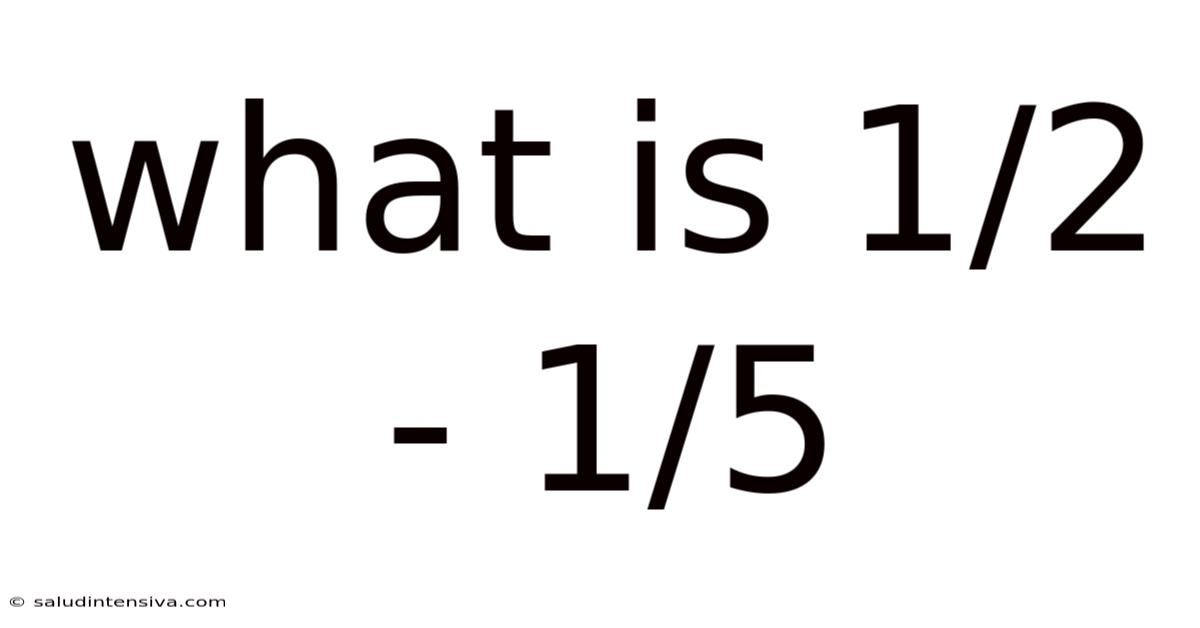
Table of Contents
Unveiling the Mystery: A Deep Dive into 1/2 - 1/5
This article explores the seemingly simple subtraction problem: 1/2 - 1/5. While the answer might appear straightforward at first glance, understanding the underlying principles of fraction subtraction opens doors to a deeper appreciation of mathematics. We'll journey through the process, exploring various methods and unraveling the conceptual intricacies involved, making this seemingly simple calculation a gateway to a richer understanding of fractions. This exploration will be beneficial for students learning basic arithmetic, as well as those seeking to refresh their foundational math skills.
Understanding Fractions: A Quick Refresher
Before tackling the subtraction, let's solidify our understanding of fractions. A fraction represents a part of a whole. It consists of two key components: the numerator (the top number) and the denominator (the bottom number). The numerator indicates how many parts we have, while the denominator indicates how many equal parts the whole is divided into. For example, in the fraction 1/2, the numerator is 1, and the denominator is 2, representing one out of two equal parts.
Understanding the concept of a common denominator is crucial for performing operations like addition and subtraction with fractions. A common denominator is a number that is a multiple of both denominators. Finding the least common denominator (LCD) simplifies the calculation and results in the simplest possible fraction.
Method 1: Finding the Least Common Denominator (LCD)
The most common and efficient method for subtracting fractions involves finding the least common denominator (LCD). This ensures the fractions are expressed in terms of the same unit, allowing for direct subtraction of the numerators.
Steps:
-
Identify the denominators: In our problem, 1/2 - 1/5, the denominators are 2 and 5.
-
Find the LCD: The LCD is the smallest number that is a multiple of both 2 and 5. In this case, it is 10. This means we need to convert both fractions to have a denominator of 10.
-
Convert the fractions:
- To convert 1/2 to a fraction with a denominator of 10, we multiply both the numerator and the denominator by 5: (1 x 5) / (2 x 5) = 5/10.
- To convert 1/5 to a fraction with a denominator of 10, we multiply both the numerator and the denominator by 2: (1 x 2) / (5 x 2) = 2/10.
-
Subtract the numerators: Now that both fractions have the same denominator, we can subtract the numerators: 5/10 - 2/10 = 3/10.
-
Simplify (if necessary): In this case, the fraction 3/10 is already in its simplest form, meaning there are no common factors between the numerator and the denominator other than 1.
Therefore, 1/2 - 1/5 = 3/10.
Method 2: Using a Visual Representation
Visual aids can significantly enhance understanding, especially when dealing with fractions. Let's visualize the subtraction using a diagram.
Imagine a rectangle representing a whole.
- 1/2: Divide the rectangle in half. Shade one half.
- 1/5: Divide the same rectangle into five equal parts. This will require dividing each of the initial halves into 2.5 parts each. However, it's easier to envision a new rectangle divided into 10 equal parts. Shading 2 out of 10 parts represents 1/5.
Subtracting 1/5 from 1/2 visually involves removing the shaded portion representing 1/5 (2 parts out of 10) from the shaded portion representing 1/2 (5 parts out of 10). This leaves 3 shaded parts out of 10, representing 3/10.
Method 3: Converting to Decimals
Another approach involves converting the fractions to decimals before performing the subtraction.
- 1/2: 1 divided by 2 = 0.5
- 1/5: 1 divided by 5 = 0.2
Subtracting the decimals: 0.5 - 0.2 = 0.3.
Converting the decimal back to a fraction: 0.3 = 3/10.
The Importance of Understanding the Process
While the answer, 3/10, is relatively simple to obtain, the process of arriving at that answer is significantly more important. Understanding the concept of equivalent fractions, finding the LCD, and the underlying logic of fraction subtraction builds a solid foundation for more complex mathematical concepts. This knowledge extends far beyond simple arithmetic and becomes crucial in algebra, calculus, and numerous other mathematical fields.
Expanding the Concept: Working with More Complex Fractions
The principles illustrated with 1/2 - 1/5 can be applied to more complex fraction subtraction problems. The key always lies in finding the LCD and ensuring that the fractions are expressed with the same denominator before subtracting the numerators.
For example, let's consider the subtraction: 3/4 - 2/7
-
Find the LCD: The LCD of 4 and 7 is 28.
-
Convert the fractions:
- 3/4 = (3 x 7) / (4 x 7) = 21/28
- 2/7 = (2 x 4) / (7 x 4) = 8/28
-
Subtract the numerators: 21/28 - 8/28 = 13/28
Frequently Asked Questions (FAQ)
Q: Why is finding the LCD important?
A: Finding the LCD ensures that we are subtracting like units. Just as we can't directly subtract apples from oranges, we cannot directly subtract fractions with different denominators. The LCD provides a common unit of measurement for the fractions.
Q: Can I always convert fractions to decimals before subtracting?
A: While converting to decimals is a viable method for some fraction subtraction problems, it's not always the most efficient or accurate. Repeating decimals can lead to rounding errors, and the conversion process itself can be time-consuming for more complex fractions.
Q: What if the resulting fraction can be simplified?
A: After subtracting the numerators, always check if the resulting fraction can be simplified. This involves finding the greatest common divisor (GCD) of the numerator and the denominator and dividing both by the GCD. For example, 6/12 can be simplified to 1/2 by dividing both the numerator and denominator by 6 (their GCD).
Q: Are there other methods for subtracting fractions?
A: While the LCD method is the most efficient and commonly used, there are other approaches, such as using a common numerator or using visual models like fraction circles or bars. However, the LCD method is generally preferred for its efficiency and broad applicability.
Conclusion: Beyond the Numbers
The seemingly straightforward problem of 1/2 - 1/5 provides a valuable opportunity to delve into the fundamental principles of fraction arithmetic. By mastering the techniques of finding the LCD and applying these concepts, you build a strong foundation for more complex mathematical challenges. The focus should not solely be on obtaining the correct answer (3/10), but on understanding the underlying reasoning and the broader mathematical concepts involved. This understanding is key to not just solving similar problems, but also to confidently tackling more advanced mathematical topics in the future. The journey of understanding fractions is a building block for mathematical proficiency, and each step, even the seemingly simple ones, contributes to a greater understanding of the mathematical world. Remember to practice consistently, and don’t hesitate to explore different approaches to reinforce your understanding. The beauty of mathematics lies in its logic and structure, and with practice, you will find yourself navigating the complexities of numbers with greater ease and confidence.
Latest Posts
Latest Posts
-
Cross Sectional Area Pipe Calculator
Sep 19, 2025
-
What 10 Percent Of 100
Sep 19, 2025
-
Is 58 A Prime Number
Sep 19, 2025
-
1 1 Kg How Many Pounds
Sep 19, 2025
-
7 To Power Of 6
Sep 19, 2025
Related Post
Thank you for visiting our website which covers about What Is 1/2 - 1/5 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.