What Is 1 2 Squared
saludintensiva
Sep 19, 2025 · 7 min read
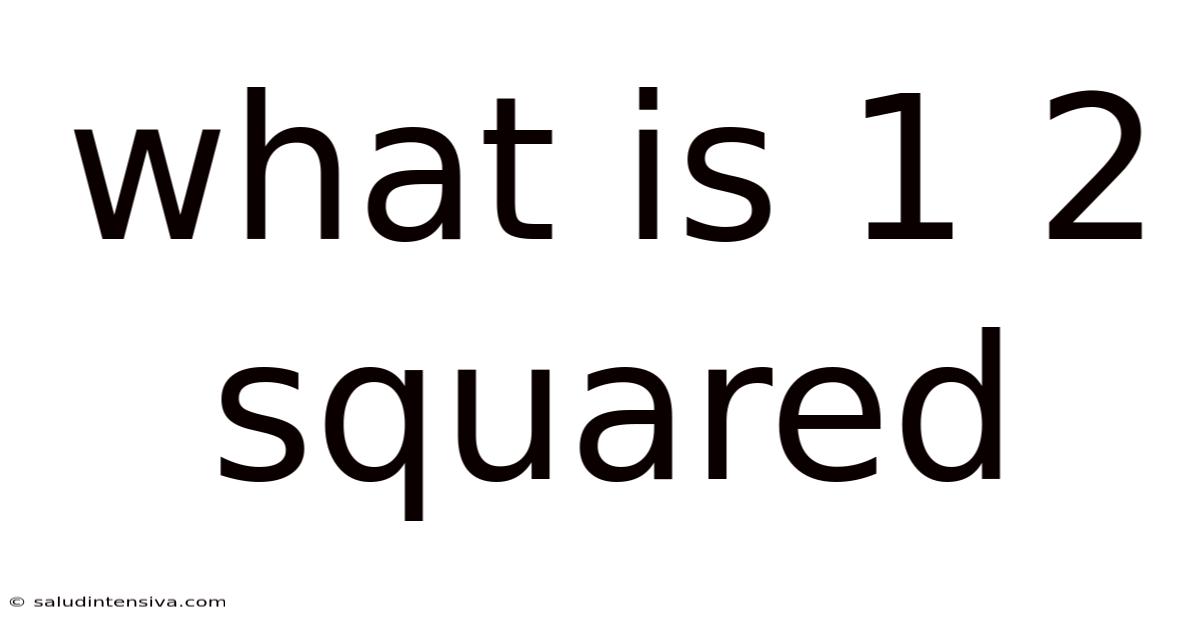
Table of Contents
Decoding 1 2 Squared: Understanding the Concept and its Applications
What does "1 2 squared" actually mean? This seemingly simple question opens the door to a fascinating exploration of mathematical concepts, particularly those involving exponents, order of operations, and their real-world applications. This article will delve deep into the meaning of this expression, examining its interpretation, calculations, and relevance in various mathematical fields. We'll cover everything from basic arithmetic to more advanced applications, ensuring a comprehensive understanding for readers of all levels.
Understanding the Basics: Exponents and Order of Operations
Before we tackle "1 2 squared," let's establish a solid foundation. The term "squared" implies raising a number to the power of 2. In mathematical notation, this is represented by a superscript "2". For example, 5 squared is written as 5², which means 5 multiplied by itself: 5 x 5 = 25.
The phrase "1 2 squared" presents a slight ambiguity, which needs careful attention. The ambiguity arises from the lack of explicit operators between the numbers. Does it mean (1 x 2)² or 1 x (2²)? The answer hinges on the order of operations, often remembered by the acronym PEMDAS (Parentheses, Exponents, Multiplication and Division, Addition and Subtraction). This dictates that we should handle exponents before multiplication.
Interpretation 1: (1 x 2)²
If we interpret "1 2 squared" as (1 x 2)², we're following PEMDAS rigorously. First, we perform the operation within the parentheses: 1 x 2 = 2. Then, we square the result: 2² = 2 x 2 = 4. Therefore, under this interpretation, 1 2 squared equals 4.
This interpretation prioritizes clarity and avoids potential misunderstandings. Writing the expression explicitly as (1 x 2)² removes any doubt regarding the intended calculation. This is the preferred method in formal mathematical notation to avoid ambiguity.
Interpretation 2: 1 x (2²)
Another possible interpretation is 1 x (2²). Here, we first square 2, resulting in 2² = 4. Then, we multiply this result by 1: 1 x 4 = 4. In this case, 1 2 squared also equals 4.
Although this interpretation yields the same result, it relies on an implicit multiplication between 1 and the result of 2². It’s less explicit and potentially more prone to misinterpretations. While mathematically correct in this specific instance, it's advisable to always use parentheses to make the order of operations completely clear.
Expanding the Concept: Generalizing Exponents and their Properties
The concept of squaring, or raising to the power of 2, is a specific case of exponentiation. Exponentiation is a mathematical operation that involves raising a base number to a certain power (exponent). The expression b<sup>n</sup> denotes b raised to the power of n, which means b is multiplied by itself n times.
Several key properties of exponents are crucial for understanding more complex mathematical calculations:
-
Product of Powers: b<sup>m</sup> x b<sup>n</sup> = b<sup>(m+n)</sup>. When multiplying two numbers with the same base, you can add their exponents.
-
Quotient of Powers: b<sup>m</sup> / b<sup>n</sup> = b<sup>(m-n)</sup>. When dividing two numbers with the same base, you subtract their exponents.
-
Power of a Power: (b<sup>m</sup>)<sup>n</sup> = b<sup>(m x n)</sup>. When raising a power to another power, you multiply the exponents.
-
Power of a Product: (ab)<sup>n</sup> = a<sup>n</sup>b<sup>n</sup>. When raising a product to a power, you raise each factor to that power.
-
Power of a Quotient: (a/b)<sup>n</sup> = a<sup>n</sup>/b<sup>n</sup>. When raising a quotient to a power, you raise both the numerator and denominator to that power.
These properties are fundamental in simplifying and solving numerous mathematical problems, from basic algebra to advanced calculus.
Applications of Squaring in Real-World Scenarios
The concept of squaring, and more broadly, exponentiation, is not just a theoretical exercise. It has numerous real-world applications across various fields:
-
Geometry: Calculating the area of a square directly uses squaring. If a square has sides of length s, its area is s². Similarly, squaring is used in calculating areas of circles (using the radius in the formula πr²) and volumes of cubes (s³).
-
Physics: Many physics equations involve squaring. For example, Newton's second law of motion (F = ma) can be combined with other equations to show that the kinetic energy of an object is proportional to the square of its velocity. Similarly, the distance an object falls under gravity is proportional to the square of the time it has been falling.
-
Engineering: Structural engineers utilize squaring and higher-order exponents when calculating stresses and strains on building materials. The strength of a beam, for example, is often related to the square of its depth.
-
Finance: Compound interest calculations involve exponents. The future value of an investment is calculated using a formula that includes the principal amount raised to a power representing the number of compounding periods.
-
Computer Science: Computational complexity analysis often involves exponents to describe the efficiency of algorithms. For example, an algorithm with O(n²) complexity indicates that its execution time increases proportionally to the square of the input size.
Beyond Squaring: Higher-Order Exponents and Their Significance
While we've focused on squaring (raising to the power of 2), the concept extends to higher-order exponents. Cubing (raising to the power of 3) is used to calculate volumes of cubes and other three-dimensional shapes. Higher exponents are used in more complex mathematical models and calculations.
For instance, in statistics, higher-order moments (like skewness and kurtosis) of a probability distribution are calculated using higher-order powers. These moments provide valuable insights into the shape and characteristics of the distribution.
Addressing Potential Confusion: Common Misconceptions
One common misconception related to exponents is the incorrect application of the distributive property. The distributive property states that a(b + c) = ab + ac. However, this does not apply to exponents: (a + b)² ≠ a² + b². Instead, (a + b)² = (a + b)(a + b) = a² + 2ab + b². This is a fundamental error that should be carefully avoided.
Another potential source of confusion lies in negative and fractional exponents. Understanding negative exponents (e.g., 2⁻²) requires understanding their reciprocal relationship with positive exponents (2⁻² = 1/2² = 1/4). Similarly, fractional exponents (e.g., 4<sup>1/2</sup>) represent roots (4<sup>1/2</sup> = √4 = 2). A firm grasp of these concepts is vital for tackling more advanced mathematical problems.
Frequently Asked Questions (FAQ)
Q1: What is the difference between 1² + 2² and (1 + 2)²?
A1: 1² + 2² = 1 + 4 = 5, while (1 + 2)² = 3² = 9. These are not equal because squaring is not distributive over addition.
Q2: How do I calculate 10<sup>5</sup>?
A2: 10<sup>5</sup> means 10 multiplied by itself five times: 10 x 10 x 10 x 10 x 10 = 100,000.
Q3: What is the significance of the order of operations (PEMDAS)?
A3: PEMDAS ensures that mathematical expressions are evaluated consistently and unambiguously, yielding the same result regardless of who performs the calculation. Without a standard order, multiple interpretations and potentially incorrect answers are possible.
Q4: Can you explain fractional exponents in more detail?
A4: Fractional exponents represent roots. For example, x<sup>m/n</sup> is the nth root of x<sup>m</sup>. So, 8<sup>2/3</sup> is the cube root of 8² (the cube root of 64), which equals 4.
Conclusion
Understanding the concept of "1 2 squared," while seemingly straightforward, opens a door to a broader comprehension of exponents, order of operations, and their significance in various fields. By grasping the fundamental principles and properties of exponents, we can effectively tackle more complex mathematical challenges and appreciate the power and elegance of mathematical concepts in explaining and predicting real-world phenomena. The key takeaway is the importance of precise notation and a strong understanding of the order of operations to avoid ambiguity and ensure accurate calculations. The consistent application of PEMDAS and a thorough understanding of exponent properties are crucial for success in mathematics and related disciplines.
Latest Posts
Latest Posts
-
Printable Military Time Conversion Table
Sep 19, 2025
-
How Long Is 181 Minutes
Sep 19, 2025
-
Write As A Decimal 6
Sep 19, 2025
-
Greatest Common Factor Of 50
Sep 19, 2025
-
Lcm Of 120 And 68
Sep 19, 2025
Related Post
Thank you for visiting our website which covers about What Is 1 2 Squared . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.