What Is 1/3 + 2/9
saludintensiva
Sep 22, 2025 · 5 min read
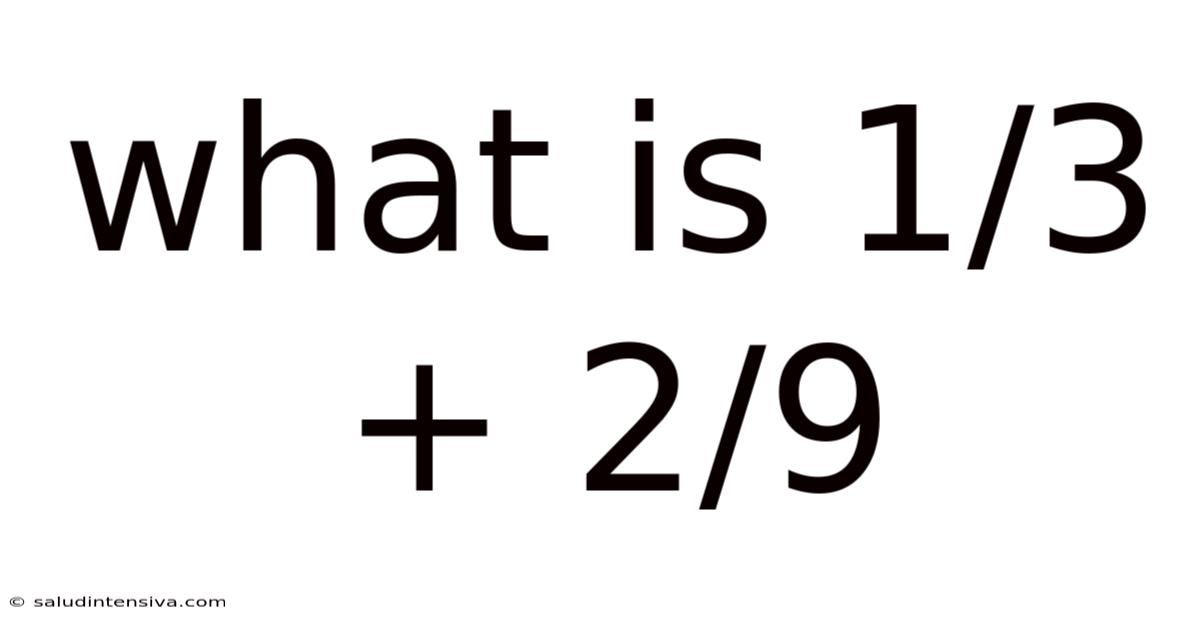
Table of Contents
Unveiling the Mystery: What is 1/3 + 2/9? A Deep Dive into Fraction Addition
Understanding fractions is a cornerstone of mathematics, crucial for everything from baking a cake to calculating complex engineering projects. This article will delve into the seemingly simple problem of adding 1/3 and 2/9, not just providing the answer, but exploring the underlying principles and offering a comprehensive understanding of fraction addition. We will cover the steps involved, explain the mathematical reasoning, address common misconceptions, and even explore some real-world applications. By the end, you'll not only know the solution to 1/3 + 2/9 but also possess a confident grasp of fraction addition in general.
Understanding Fractions: A Quick Refresher
Before we tackle the problem at hand, let's review the basics of fractions. A fraction represents a part of a whole. It's composed of two numbers: the numerator (the top number) and the denominator (the bottom number). The numerator tells us how many parts we have, while the denominator tells us how many equal parts the whole is divided into. For example, in the fraction 1/3, the numerator is 1 and the denominator is 3, meaning we have one out of three equal parts.
Finding a Common Denominator: The Key to Fraction Addition
Adding or subtracting fractions requires a crucial step: finding a common denominator. This is because you can only directly add or subtract parts that are of the same size. Imagine trying to add one apple and two oranges – you can't simply say you have three "fruit," you need a common unit. Similarly, with fractions, we need to express both fractions with the same denominator before we can add their numerators.
In our problem, 1/3 + 2/9, the denominators are 3 and 9. We need to find the least common multiple (LCM) of 3 and 9. The LCM is the smallest number that is a multiple of both 3 and 9. In this case, the LCM is 9.
Converting Fractions to a Common Denominator
Now that we have our common denominator (9), we need to convert both fractions so they have this denominator. For 2/9, this is already done. For 1/3, we need to multiply both the numerator and the denominator by 3 to get an equivalent fraction with a denominator of 9:
(1/3) * (3/3) = 3/9
Notice that multiplying both the numerator and denominator by the same number doesn't change the value of the fraction; it only changes its representation. It's like changing dollars to cents – the value remains the same, only the unit changes.
Adding the Fractions: The Final Step
Now that both fractions have the same denominator (9), we can simply add their numerators:
3/9 + 2/9 = (3 + 2) / 9 = 5/9
Therefore, the answer to 1/3 + 2/9 is 5/9.
Visualizing Fraction Addition
Understanding fractions can be easier when visualized. Imagine a pizza cut into nine slices. 1/3 of the pizza would be three slices (9 slices total divided into three equal groups of three). 2/9 of the pizza would be two slices. Adding them together, you would have five slices out of nine, or 5/9 of the pizza.
Dealing with More Complex Fraction Addition Problems
The process outlined above can be extended to more complex fraction addition problems. The key steps remain the same:
-
Find the least common multiple (LCM) of the denominators. This is the new common denominator. For larger numbers, methods like prime factorization can help find the LCM efficiently.
-
Convert each fraction to an equivalent fraction with the common denominator. This involves multiplying both the numerator and denominator of each fraction by the appropriate number.
-
Add the numerators. Keep the common denominator the same.
-
Simplify the resulting fraction (if possible). This means reducing the fraction to its lowest terms by dividing both the numerator and denominator by their greatest common divisor (GCD).
Addressing Common Misconceptions
A common mistake in fraction addition is adding the numerators and the denominators directly. This is incorrect. Remember, you're adding parts of a whole, and those parts must be of the same size (i.e., have the same denominator).
Real-World Applications of Fraction Addition
Fraction addition is surprisingly prevalent in everyday life. Here are a few examples:
- Cooking and Baking: Recipes often require fractions of ingredients. Adding fractions is essential to ensure accurate measurements.
- Construction and Engineering: Precise calculations involving fractions are crucial in building and engineering projects to ensure structural integrity and proper measurements.
- Finance: Calculating portions of budgets or investments often involves working with fractions.
- Data Analysis: Representing and manipulating data often uses fractions and proportions.
Frequently Asked Questions (FAQ)
Q: What if the fractions have different denominators that don't have a simple common denominator?
A: If finding the LCM isn't immediately obvious, you can always multiply the denominators together to get a common denominator. However, this may lead to a larger fraction that requires simplification afterward. Using the LCM always results in the simplest form.
Q: What if the resulting fraction is an improper fraction (numerator larger than the denominator)?
A: An improper fraction can be converted into a mixed number. A mixed number consists of a whole number and a proper fraction. For example, 11/9 can be expressed as 1 2/9 (one and two-ninths).
Q: Can I use a calculator to add fractions?
A: Yes, many calculators have the ability to add fractions. However, understanding the underlying process is essential for grasping the concept and solving problems without relying on a calculator.
Q: Are there other methods for adding fractions besides finding a common denominator?
A: While finding a common denominator is the most common and widely understood method, other advanced techniques exist for adding fractions, but they are generally introduced at higher levels of mathematics.
Conclusion: Mastering Fraction Addition
Adding fractions, even seemingly simple ones like 1/3 + 2/9, is a fundamental skill in mathematics. By understanding the principles of finding a common denominator, converting fractions, and adding numerators, you can confidently solve a wide range of fraction addition problems. This skill is not just a classroom exercise; it's a tool applicable to numerous aspects of everyday life, from cooking to complex engineering projects. Remember to practice regularly, and you'll soon master this essential mathematical skill. The solution to 1/3 + 2/9 is 5/9, but the true value lies in understanding the why behind the answer.
Latest Posts
Latest Posts
-
Knots To Feet Per Second
Sep 22, 2025
-
100 000 In Exponential Form
Sep 22, 2025
-
40 Weeks From January 15
Sep 22, 2025
-
How Much For Cement Slab
Sep 22, 2025
-
98 6 F To C
Sep 22, 2025
Related Post
Thank you for visiting our website which covers about What Is 1/3 + 2/9 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.