What Is 1/3 And 1/3
saludintensiva
Sep 18, 2025 · 6 min read
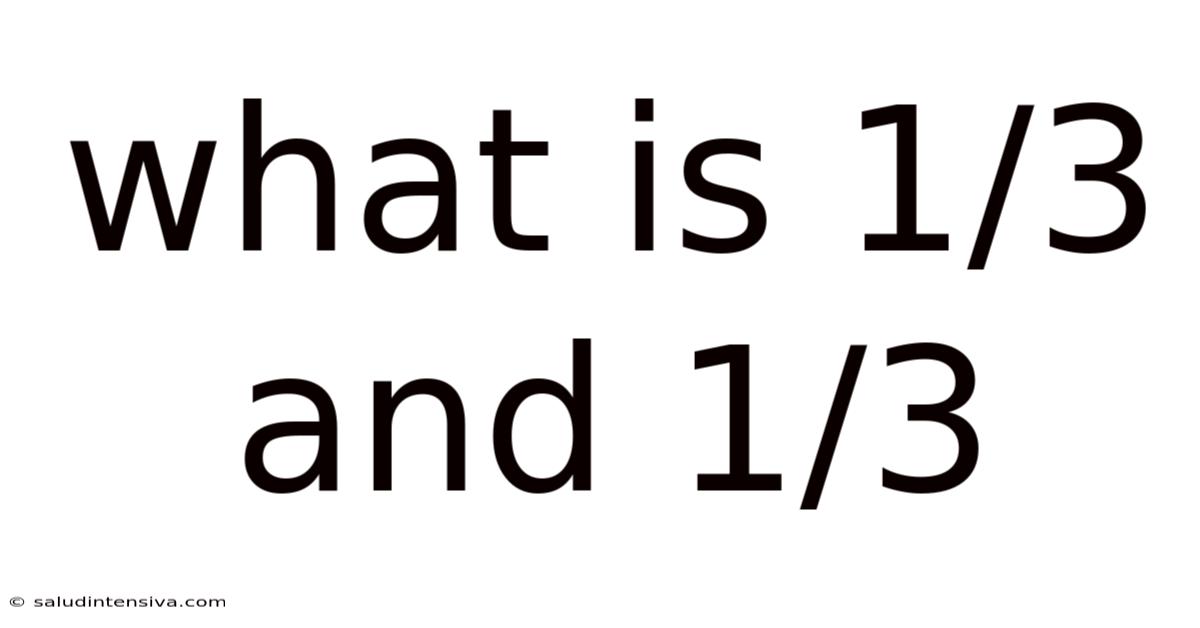
Table of Contents
Decoding the Mystery of 1/3 + 1/3: A Deep Dive into Fractions
What is 1/3 + 1/3? This seemingly simple question forms the bedrock of fractional arithmetic and understanding. While the answer might seem obvious to some, a deeper exploration reveals fundamental concepts crucial for mastering mathematics, particularly in algebra, calculus, and beyond. This article will not only answer the question directly but also delve into the underlying principles of fractions, providing a comprehensive understanding for learners of all levels. We'll explore different methods of solving this problem, discuss the importance of common denominators, and even touch upon the surprising complexities that can arise when dealing with fractions – even simple ones like these.
Introduction to Fractions: Understanding the Parts
Before tackling the addition, let's establish a solid foundation in fractional understanding. A fraction represents a part of a whole. It's expressed as a ratio of two numbers: the numerator (the top number) and the denominator (the bottom number). The denominator tells us how many equal parts the whole is divided into, while the numerator tells us how many of those parts we're considering.
In the fraction 1/3, the denominator (3) indicates that the whole is divided into three equal parts. The numerator (1) indicates that we are considering only one of those three parts. Imagine a pizza cut into three equal slices. 1/3 represents one slice of that pizza.
Adding Fractions: The Common Denominator Rule
Adding fractions requires a crucial step: finding a common denominator. The common denominator is a number that is a multiple of both denominators in the fractions being added. This step ensures we're adding like quantities – comparing apples to apples, not apples to oranges.
In our case, we're adding 1/3 + 1/3. Both fractions have the same denominator, 3. This means we already have a common denominator! This simplifies the addition considerably.
Solving 1/3 + 1/3: A Step-by-Step Approach
Since we already have a common denominator, the addition process is straightforward:
-
Keep the denominator the same: The denominator remains 3.
-
Add the numerators: Add the numerators together: 1 + 1 = 2.
-
Combine the results: The result is the sum of the numerators over the common denominator: 2/3.
Therefore, 1/3 + 1/3 = 2/3. This means that if you have one-third of a pizza and you add another one-third, you have two-thirds of a pizza.
Visual Representation: Understanding Fractions through Pictures
Visual aids can significantly improve the understanding of fractions. Imagine two identical circles, each divided into three equal parts. Shade one part in the first circle (representing 1/3) and one part in the second circle (representing another 1/3). Combining the shaded parts shows that we have shaded two out of the six total parts, which is equivalent to 2/3.
Extending the Concept: Adding Fractions with Different Denominators
Let's extend our understanding to adding fractions with different denominators. For example, consider 1/2 + 1/4. Here, we don't have a common denominator. We need to find the least common multiple (LCM) of 2 and 4, which is 4.
-
Find the common denominator: The LCM of 2 and 4 is 4.
-
Convert the fractions: We need to rewrite the fractions with the common denominator. 1/2 is equivalent to 2/4 (multiply both numerator and denominator by 2).
-
Add the fractions: Now we have 2/4 + 1/4. Add the numerators: 2 + 1 = 3.
-
Combine the results: The sum is 3/4.
Therefore, 1/2 + 1/4 = 3/4.
The Importance of Common Denominators: A Deeper Explanation
The concept of a common denominator is crucial because it allows us to directly compare and combine fractions. Without a common denominator, we are essentially trying to add unlike units. Imagine trying to add 1 apple and 2 oranges – you can't simply add them together and get 3 of something specific. Similarly, without a common denominator, we cannot directly add fractions. The common denominator provides a standard unit of measurement for the fractions, enabling accurate addition.
Simplifying Fractions: Reducing to Lowest Terms
Sometimes, after adding fractions, the resulting fraction can be simplified. Simplification involves reducing the fraction to its lowest terms by dividing both the numerator and denominator by their greatest common divisor (GCD).
For example, if we add 2/6 + 1/6 = 3/6, we can simplify this fraction. The GCD of 3 and 6 is 3. Dividing both the numerator and denominator by 3 gives us 1/2.
Fractions in Real-World Applications
Fractions are not just abstract mathematical concepts; they have numerous real-world applications:
- Cooking and Baking: Recipes often call for fractional amounts of ingredients (e.g., 1/2 cup of sugar).
- Measurement: Measuring lengths, weights, and volumes frequently involve fractions (e.g., 2 1/2 inches).
- Finance: Calculating percentages, interest rates, and proportions involves fractional arithmetic.
- Construction and Engineering: Precise measurements and calculations in construction and engineering rely heavily on fractions.
Understanding fractions is essential for navigating these everyday scenarios effectively.
Beyond Simple Addition: Exploring More Complex Fractional Operations
While this article focuses on the addition of simple fractions, the principles discussed extend to more complex operations. Subtraction, multiplication, and division of fractions all involve similar concepts, though the methods differ slightly. For instance, multiplying fractions involves multiplying the numerators together and the denominators together, while dividing fractions involves inverting the second fraction and then multiplying.
Frequently Asked Questions (FAQs)
Q: What if the denominators are very large numbers? How do I find a common denominator?
A: For larger numbers, finding the LCM can be more challenging. One method is to find the prime factorization of each denominator and then use the highest power of each prime factor to construct the LCM. Alternatively, you can simply multiply the two denominators together, though this may not always result in the least common denominator.
Q: Can I add fractions without finding a common denominator?
A: No, you cannot accurately add fractions without a common denominator. This would be akin to adding apples and oranges, leading to an incorrect result.
Q: What is a mixed number, and how does it relate to improper fractions?
A: A mixed number combines a whole number and a fraction (e.g., 2 1/3). An improper fraction has a numerator larger than or equal to the denominator (e.g., 7/3). Mixed numbers and improper fractions represent the same quantity; 2 1/3 is equivalent to 7/3.
Q: Are there any online tools or calculators to help with fraction calculations?
A: Yes, many online calculators and tools can perform fraction addition, subtraction, multiplication, and division. These tools can be helpful for checking your work or assisting with more complex calculations.
Conclusion: Mastering Fractions – A Building Block for Mathematical Success
Understanding the addition of fractions, even seemingly simple ones like 1/3 + 1/3, is fundamental to mastering more advanced mathematical concepts. The principles of common denominators, simplification, and the relationship between fractions and real-world applications are crucial for success in various fields. While this article has provided a thorough explanation, continued practice and exploration will solidify your understanding and build confidence in tackling more complex fractional problems. Remember, mastering fractions is not just about getting the right answer; it's about understanding the underlying principles and developing a strong mathematical foundation. So keep practicing, keep exploring, and remember the power of understanding fractions – a power that extends far beyond the classroom.
Latest Posts
Latest Posts
-
Convert 75 Fahrenheit To Celsius
Sep 18, 2025
-
2 To The 6 Power
Sep 18, 2025
-
Write 1 4 As A Percent
Sep 18, 2025
-
20 4 In Decimal Form
Sep 18, 2025
-
19 4 As A Decimal
Sep 18, 2025
Related Post
Thank you for visiting our website which covers about What Is 1/3 And 1/3 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.