What Is 1/3 Of 1/5
saludintensiva
Sep 17, 2025 · 5 min read
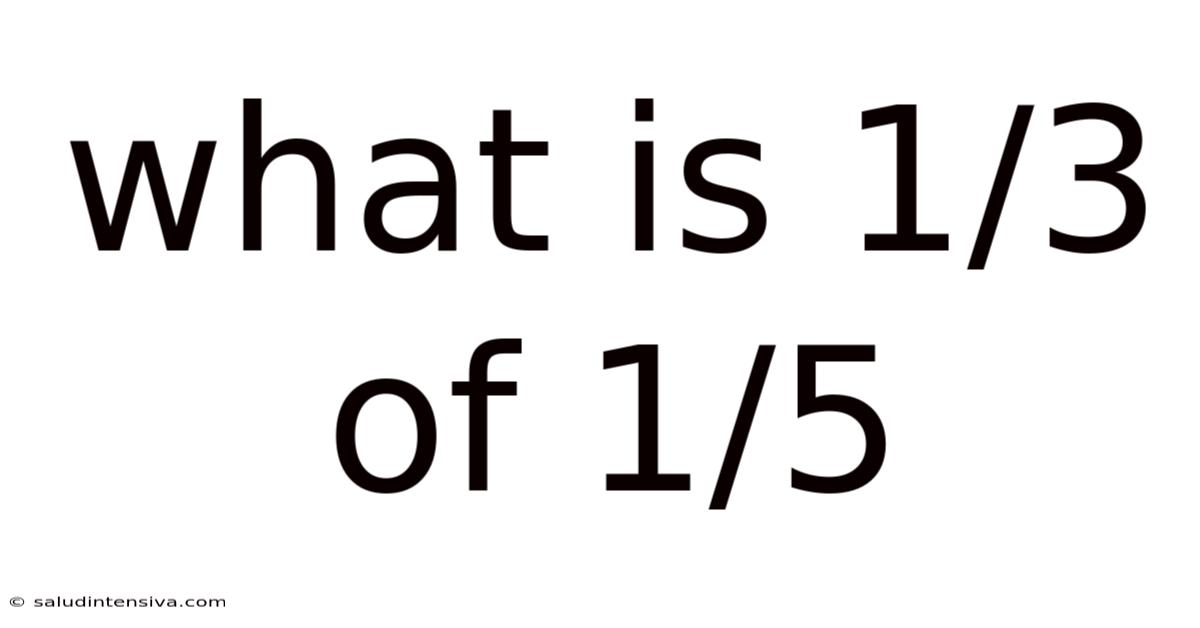
Table of Contents
What is 1/3 of 1/5? A Deep Dive into Fractions and Multiplication
Finding a fraction of another fraction might seem daunting at first, but with a clear understanding of the underlying principles, it becomes a straightforward process. This article will explore the question, "What is 1/3 of 1/5?", providing a step-by-step solution, explaining the mathematical concepts involved, and exploring the broader context of fraction multiplication. We'll delve into various methods of solving this problem, including visual representations to solidify your understanding. By the end, you'll not only know the answer but also possess the confidence to tackle similar fraction problems.
Understanding Fractions: A Quick Recap
Before we jump into the problem, let's refresh our understanding of fractions. A fraction represents a part of a whole. It's expressed as a ratio of two numbers: the numerator (top number) and the denominator (bottom number). The numerator indicates how many parts we have, while the denominator indicates how many equal parts the whole is divided into. For example, in the fraction 1/5, the numerator is 1 and the denominator is 5, meaning we have 1 part out of a total of 5 equal parts.
Visualizing the Problem: A Practical Approach
One of the best ways to understand fraction multiplication is through visualization. Let's imagine a rectangle representing a whole. To represent 1/5, we divide the rectangle into 5 equal parts and shade one of them. Now, to find 1/3 of this 1/5, we need to divide the shaded portion (1/5) into three equal parts and consider only one of those parts. This visual representation helps understand that we're finding a smaller fraction within a larger fraction.
Calculating 1/3 of 1/5: Step-by-Step Solution
To calculate 1/3 of 1/5, we perform a multiplication operation. The word "of" in mathematics often signifies multiplication. Therefore, the problem translates to (1/3) x (1/5).
Step 1: Multiply the Numerators
Multiply the numerators together: 1 x 1 = 1
Step 2: Multiply the Denominators
Multiply the denominators together: 3 x 5 = 15
Step 3: Form the Resulting Fraction
Combine the results from steps 1 and 2 to form the final fraction: 1/15
Therefore, 1/3 of 1/5 is 1/15.
The Mathematical Explanation: Why it Works
The process of multiplying fractions involves multiplying the numerators and then multiplying the denominators. This method works because fractions represent parts of a whole. When you multiply two fractions, you are essentially finding a fraction of a fraction. This process effectively combines the portions represented by each fraction.
Consider this: 1/5 already represents a portion of a whole. When you find 1/3 of that portion (1/5), you are essentially taking one-third of the already existing portion, resulting in a smaller fraction (1/15).
Alternative Methods: Different Paths to the Same Answer
While the direct multiplication method is the most straightforward, other approaches can reinforce understanding.
-
Using Decimal Representation: Convert the fractions to decimals and then multiply. 1/3 is approximately 0.333 and 1/5 is 0.2. Multiplying these gives approximately 0.0666, which is close to the decimal equivalent of 1/15. Note: This method involves approximation due to the repeating decimal nature of 1/3.
-
Visual Representation with Grids: Draw a grid with 3 rows and 5 columns (representing the denominators). Shade one column (1/5). Then, divide that shaded column into three equal parts. One of these smaller parts represents 1/15 of the total grid.
Expanding the Understanding: Generalizing Fraction Multiplication
The method of multiplying fractions applies universally. To multiply any two fractions, a/b and c/d:
- Multiply the numerators: a x c
- Multiply the denominators: b x d
- Form the result: (a x c) / (b x d)
This general approach allows you to solve a wide array of problems involving fraction multiplication.
Simplifying Fractions: Reducing to the Lowest Terms
After multiplying fractions, it's crucial to simplify the resulting fraction, if possible, by reducing it to its lowest terms. This means finding the greatest common divisor (GCD) of the numerator and denominator and dividing both by the GCD. In the case of 1/15, both 1 and 15 have a GCD of 1, meaning the fraction is already in its simplest form.
Frequently Asked Questions (FAQ)
-
Q: Can I add fractions the same way I multiply them? A: No. Adding fractions requires a common denominator. You need to find a common denominator for the fractions before adding the numerators. Multiplication of fractions does not require a common denominator.
-
Q: What if I have mixed numbers (whole numbers and fractions)? A: Convert the mixed numbers into improper fractions (where the numerator is larger than or equal to the denominator) before multiplying.
-
Q: What if one of the fractions is a whole number? A: Treat the whole number as a fraction with a denominator of 1. For example, 2 can be written as 2/1.
Conclusion: Mastering Fraction Multiplication
Understanding fraction multiplication is essential for success in mathematics. The problem of finding "1/3 of 1/5" highlights the core concept: multiply the numerators and multiply the denominators. Through visualization and step-by-step calculations, we've not only solved the specific problem but also gained a broader understanding of fraction multiplication and its applications. Remember to always simplify your answer to its lowest terms for a complete and accurate solution. With practice and a solid grasp of the fundamental principles, you'll confidently navigate the world of fractions and their operations. Keep practicing, and you'll become proficient in handling even more complex fraction problems. The key is to break down the problem into manageable steps and visualize the process. Don't hesitate to use visual aids or different methods to reinforce your understanding. Mastering fractions is a stepping stone to success in higher-level mathematics.
Latest Posts
Latest Posts
-
200 Percent In Decimal Form
Sep 17, 2025
-
17 3 As A Mixed Number
Sep 17, 2025
-
1 2 5 As A Percent
Sep 17, 2025
-
Adding Numbers With Scientific Notation
Sep 17, 2025
-
What Is 75f In C
Sep 17, 2025
Related Post
Thank you for visiting our website which covers about What Is 1/3 Of 1/5 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.