What Is 1/3 Of 21
saludintensiva
Sep 24, 2025 · 5 min read
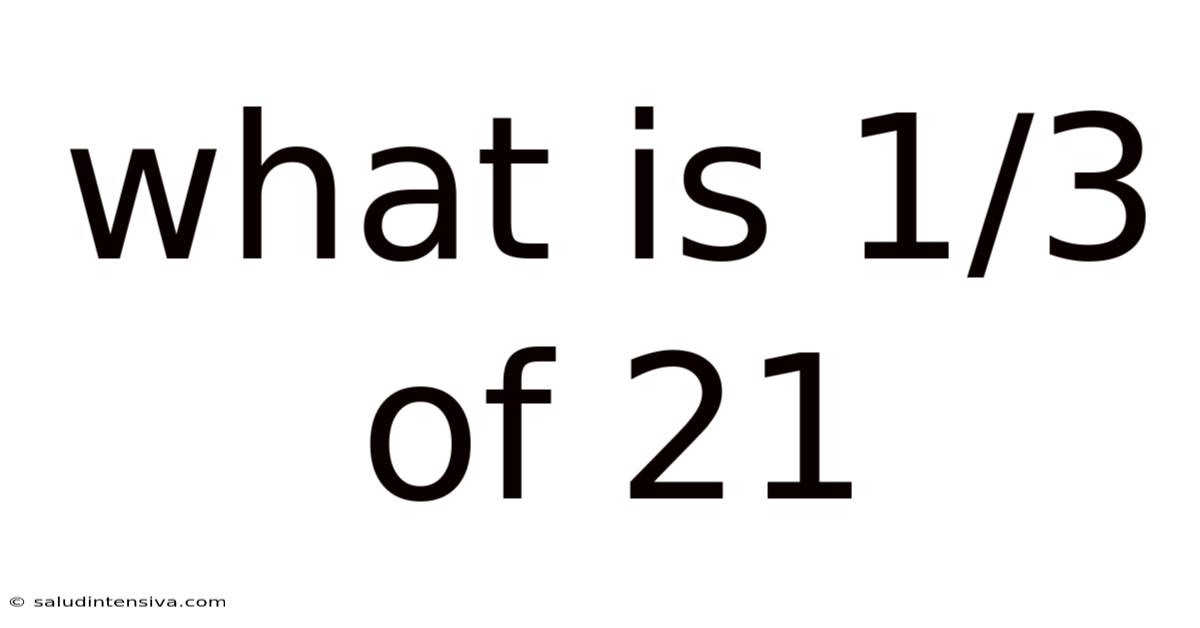
Table of Contents
What is 1/3 of 21? A Deep Dive into Fractions and Their Applications
Finding 1/3 of 21 might seem like a simple arithmetic problem, suitable only for elementary school students. However, understanding this seemingly basic calculation opens doors to a broader comprehension of fractions, their significance in various fields, and the underlying mathematical principles involved. This article will not only answer the question "What is 1/3 of 21?" but also delve into the conceptual understanding of fractions, explore different methods to solve similar problems, and discuss real-world applications where this type of calculation is crucial.
Understanding Fractions: A Foundational Concept
Before tackling the problem, let's establish a solid understanding of what fractions represent. A fraction is a part of a whole. It's expressed as a ratio of two numbers: the numerator (the top number) and the denominator (the bottom number). The denominator indicates the total number of equal parts the whole is divided into, while the numerator represents the number of those parts being considered. In the fraction 1/3, the denominator, 3, indicates that the whole is divided into three equal parts, and the numerator, 1, signifies that we are considering one of those three parts.
Understanding this concept is crucial for solving any problem involving fractions. It's not just about memorizing formulas; it's about visualizing the parts relative to the whole. Imagine a pizza cut into three equal slices. 1/3 of the pizza represents one of those slices.
Calculating 1/3 of 21: Multiple Approaches
Now, let's address the core question: What is 1/3 of 21? There are several ways to approach this calculation:
1. Division Method: The most straightforward method involves dividing 21 by the denominator (3). This gives us:
21 ÷ 3 = 7
Therefore, 1/3 of 21 is 7. This approach is intuitive and directly reflects the meaning of the fraction: we're dividing the whole (21) into three equal parts and taking one of them.
2. Multiplication Method: Another way to solve this is using multiplication. We can express "1/3 of 21" as a multiplication problem:
(1/3) × 21
To multiply a fraction by a whole number, we multiply the numerator by the whole number and keep the denominator the same:
(1 × 21) / 3 = 21/3
Then, we simplify the fraction by dividing the numerator by the denominator:
21 ÷ 3 = 7
Again, we arrive at the answer: 7. This method is particularly helpful when dealing with more complex fraction problems.
3. Visual Representation: For a more intuitive understanding, especially for beginners, visualizing the problem can be very helpful. Imagine 21 objects arranged in three equal rows. Each row would contain 21 ÷ 3 = 7 objects. One of these rows represents 1/3 of the total, which is 7.
Expanding the Concept: Fractions and Their Applications
The seemingly simple problem of finding 1/3 of 21 extends far beyond basic arithmetic. Understanding fractions is fundamental in numerous fields:
-
Cooking and Baking: Recipes often require fractional measurements. For example, a recipe might call for 2/3 cup of flour or 1/4 teaspoon of salt. Accurate fraction calculation ensures the dish turns out correctly.
-
Construction and Engineering: Precision is paramount in these fields. Fractions are essential for accurate measurements, ensuring proper fitting of components and structural integrity. Calculating the proportions of materials or determining angles frequently involves fractions.
-
Finance and Budgeting: Fractions are integral to understanding financial concepts like percentages, interest rates, and stock prices. For example, a 1/3 discount represents a reduction of one-third of the original price.
-
Data Analysis and Statistics: Fractions and their decimal equivalents are widely used to represent proportions and probabilities. Understanding fractions is crucial for interpreting data and drawing meaningful conclusions.
-
Computer Science and Programming: Fractions and their representations (floating-point numbers) are fundamental in computer programming for tasks such as image processing, game development, and scientific simulations.
Dealing with More Complex Fraction Problems
Let's consider some slightly more challenging scenarios involving fractions:
1. Finding a Fraction of a Fraction: What is 1/2 of 2/3? We can solve this by multiplying the fractions:
(1/2) × (2/3) = (1 × 2) / (2 × 3) = 2/6 = 1/3
2. Finding a Fraction of a Decimal: What is 1/3 of 21.6? First, we convert the decimal to a fraction: 21.6 = 216/10. Then, we multiply:
(1/3) × (216/10) = 216/30 = 72/10 = 7.2
3. Mixed Numbers: A mixed number combines a whole number and a fraction (e.g., 2 1/3). To find a fraction of a mixed number, we first convert it to an improper fraction. For instance, to find 1/3 of 2 1/3, we first convert 2 1/3 to 7/3:
(1/3) × (7/3) = 7/9
Frequently Asked Questions (FAQ)
-
Q: What if the numerator is larger than the denominator? A: This results in an improper fraction, which is greater than 1. It can be converted into a mixed number by dividing the numerator by the denominator. For example, 7/3 is an improper fraction equal to the mixed number 2 1/3.
-
Q: How do I add or subtract fractions? A: To add or subtract fractions with the same denominator, add or subtract the numerators and keep the denominator the same. If the denominators are different, you need to find a common denominator before performing the operation.
-
Q: How do I convert a fraction to a decimal? A: Divide the numerator by the denominator. For example, 1/3 = 0.333... (a repeating decimal).
-
Q: How do I convert a decimal to a fraction? A: Write the decimal as a fraction with a power of 10 as the denominator. Then, simplify the fraction. For example, 0.75 = 75/100 = 3/4.
Conclusion: Beyond the Numbers
Finding 1/3 of 21 is more than just a simple calculation; it's a gateway to understanding the broader world of fractions and their significance in various aspects of life. Mastering the concepts of fractions is not merely about passing a math test; it's about equipping oneself with a crucial skill applicable across numerous disciplines. By understanding the underlying principles and exploring different methods of calculation, we can confidently tackle more complex fraction problems and appreciate their crucial role in our daily lives and various fields of study and profession. From baking a cake to designing a bridge, understanding fractions is a fundamental building block for success.
Latest Posts
Latest Posts
-
2 12 As A Fraction
Sep 24, 2025
-
Function Notation And Evaluating Functions
Sep 24, 2025
-
Pace For 5 Hour Marathon
Sep 24, 2025
-
19 Out Of 25 Percent
Sep 24, 2025
-
16 In Concrete Form Tube
Sep 24, 2025
Related Post
Thank you for visiting our website which covers about What Is 1/3 Of 21 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.