What Is 1/3 Times 2/3
saludintensiva
Sep 15, 2025 · 6 min read
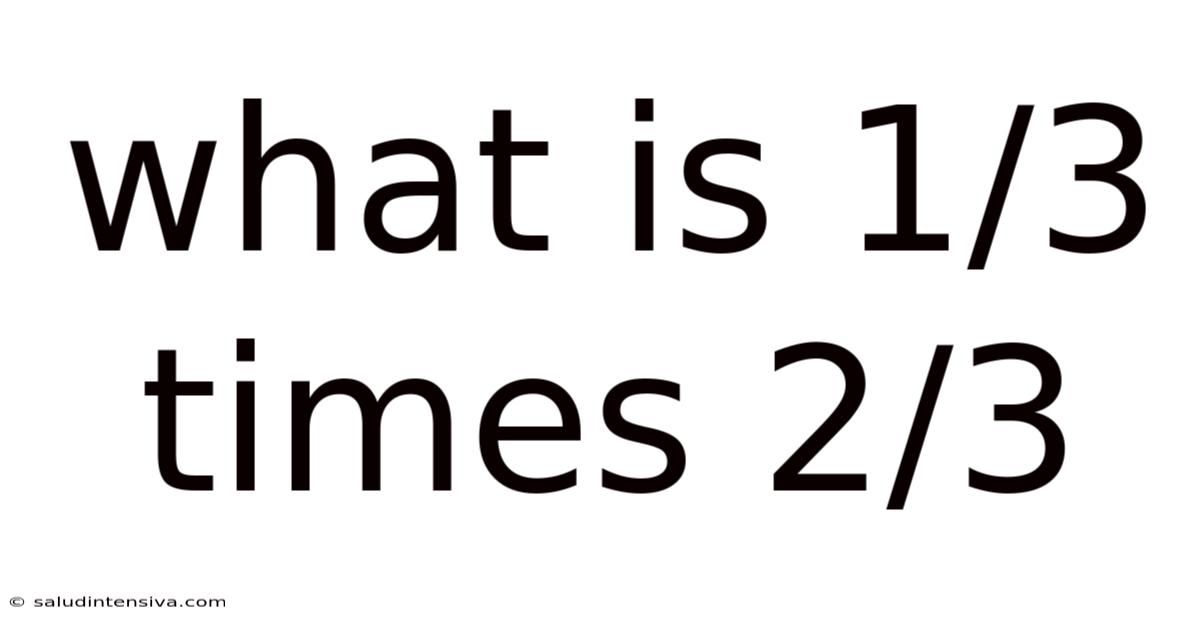
Table of Contents
What is 1/3 times 2/3? A Deep Dive into Fraction Multiplication
This article will comprehensively explain how to multiply fractions, using the example of 1/3 times 2/3. We'll explore the fundamental principles behind fraction multiplication, provide step-by-step instructions, delve into the underlying mathematical concepts, address frequently asked questions, and offer insightful examples to solidify your understanding. Understanding fraction multiplication is crucial for a solid foundation in mathematics and its various applications.
Introduction: Understanding Fractions
Before tackling the multiplication of 1/3 and 2/3, let's refresh our understanding of fractions. A fraction represents a part of a whole. It is expressed as a ratio of two numbers: the numerator (the top number) and the denominator (the bottom number). The denominator tells us how many equal parts the whole is divided into, while the numerator indicates how many of those parts we are considering. For example, in the fraction 1/3, the denominator 3 means the whole is divided into three equal parts, and the numerator 1 means we are considering one of those parts.
Multiplying Fractions: A Step-by-Step Guide
Multiplying fractions is a relatively straightforward process. Here's how to calculate 1/3 times 2/3:
Step 1: Multiply the Numerators
The first step is to multiply the numerators together. In our example, this means multiplying 1 (the numerator of 1/3) by 2 (the numerator of 2/3).
1 x 2 = 2
Step 2: Multiply the Denominators
Next, we multiply the denominators together. In this case, we multiply 3 (the denominator of 1/3) by 3 (the denominator of 2/3).
3 x 3 = 9
Step 3: Form the Resulting Fraction
Finally, we combine the results from steps 1 and 2 to form the resulting fraction. The product of the numerators becomes the new numerator, and the product of the denominators becomes the new denominator.
Therefore, 1/3 times 2/3 equals 2/9.
Visual Representation: Understanding the Process
Let's visualize this multiplication using a diagram. Imagine a square representing a whole.
-
Dividing into Thirds: Divide the square into three equal columns, representing thirds. Shading one column represents 1/3.
-
Subdividing into Ninths: Now, divide each of the three columns into three equal rows. This further subdivides the square into nine equal smaller squares, representing ninths.
-
Multiplying 1/3 by 2/3: If we take 1/3 of the square (one column) and then take 2/3 of that (two rows within the selected column), we end up with two of the nine smaller squares. This visually demonstrates that 1/3 times 2/3 equals 2/9.
The Mathematical Principle Behind Fraction Multiplication
The process of multiplying fractions is based on the concept of finding a fraction of a fraction. When we multiply 1/3 by 2/3, we are essentially finding two-thirds of one-third. This can be expressed as:
(2/3) * (1/3) = 2 * (1/3) * (1/3) = 2 * (1/9) = 2/9
This demonstrates that multiplying fractions involves multiplying the numerators and denominators separately, effectively representing the combined effect of taking a fraction of another fraction.
Simplifying Fractions: A Necessary Step
Sometimes, the resulting fraction after multiplication can be simplified. This involves finding the greatest common divisor (GCD) of the numerator and denominator and dividing both by it. The GCD is the largest number that divides both the numerator and the denominator without leaving a remainder.
In our example, 2/9, the GCD of 2 and 9 is 1. Since dividing both by 1 doesn't change the fraction, 2/9 is already in its simplest form.
More Complex Examples of Fraction Multiplication
Let's consider some more complex examples to solidify our understanding:
-
Example 1: (3/4) x (2/5) = (3 x 2) / (4 x 5) = 6/20. This fraction can be simplified by dividing both numerator and denominator by their GCD, which is 2. Therefore, 6/20 simplifies to 3/10.
-
Example 2: (5/6) x (3/10) = (5 x 3) / (6 x 10) = 15/60. The GCD of 15 and 60 is 15. Dividing both by 15 gives us 1/4.
-
Example 3: (1/2) x (1/2) x (1/2) = 1/8. This demonstrates how the principle extends to multiplying more than two fractions. We simply multiply all the numerators together and all the denominators together.
Mixed Numbers and Fraction Multiplication
A mixed number is a combination of a whole number and a fraction (e.g., 2 1/2). To multiply mixed numbers, we first convert them into improper fractions. An improper fraction is a fraction where the numerator is greater than or equal to the denominator.
For example, let's multiply 1 1/2 by 2/3:
-
Convert Mixed Number to Improper Fraction: 1 1/2 = (1 x 2 + 1) / 2 = 3/2
-
Multiply the Fractions: (3/2) x (2/3) = (3 x 2) / (2 x 3) = 6/6 = 1
Applications of Fraction Multiplication in Real Life
Fraction multiplication is widely used in various real-life situations:
-
Cooking: Scaling recipes up or down often requires multiplying fractions. For example, if a recipe calls for 1/2 cup of flour and you want to double the recipe, you'll multiply 1/2 by 2.
-
Construction: Calculating material quantities for projects often involves fractions. For example, determining the amount of lumber needed might require multiplying fractions to account for cuts and waste.
-
Finance: Calculating interest or discounts often involves fraction multiplication.
-
Probability: Calculating probabilities often involves multiplying fractions representing the chances of different events occurring.
Frequently Asked Questions (FAQ)
-
Q: What happens if I multiply a fraction by 0?
- A: Multiplying any fraction by 0 always results in 0.
-
Q: Can I multiply fractions with different denominators?
- A: Yes, you can multiply fractions with different denominators directly using the method described above. You only need to simplify the resulting fraction if possible.
-
Q: What if one of the numbers is a whole number?
- A: Treat the whole number as a fraction with a denominator of 1. For example, 2 x 1/3 = (2/1) x (1/3) = 2/3.
-
Q: Why do we multiply the numerators and the denominators separately?
- A: This method reflects the underlying mathematical principle of finding a fraction of a fraction. It's a concise way of representing this operation.
-
Q: Is there an easier way to multiply fractions?
- A: The method described above is the standard and most efficient way to multiply fractions. However, if possible, you can simplify fractions before multiplying to reduce the size of the numbers involved and simplify the simplification process afterward. This technique is called cancelling.
Conclusion: Mastering Fraction Multiplication
Mastering fraction multiplication is essential for building a strong foundation in mathematics. The process is straightforward: multiply the numerators, multiply the denominators, and simplify the resulting fraction if necessary. By understanding the underlying mathematical principles and practicing with various examples, you can confidently tackle fraction multiplication in various contexts, from simple arithmetic to more complex applications in real-world scenarios. Remember the visual representations can aid in solidifying your understanding and making the concept more intuitive. Remember to practice regularly to reinforce your skills and build confidence in your ability to work with fractions.
Latest Posts
Latest Posts
-
2 3 4 3 4
Sep 15, 2025
-
10 019 Sqft To Acres
Sep 15, 2025
-
What Is 3 8 Simplified
Sep 15, 2025
-
3 8 Plus 3 8
Sep 15, 2025
-
75 Fahrenheit Convert To Celsius
Sep 15, 2025
Related Post
Thank you for visiting our website which covers about What Is 1/3 Times 2/3 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.