What Is 1/4 / 3/4
saludintensiva
Sep 09, 2025 · 5 min read
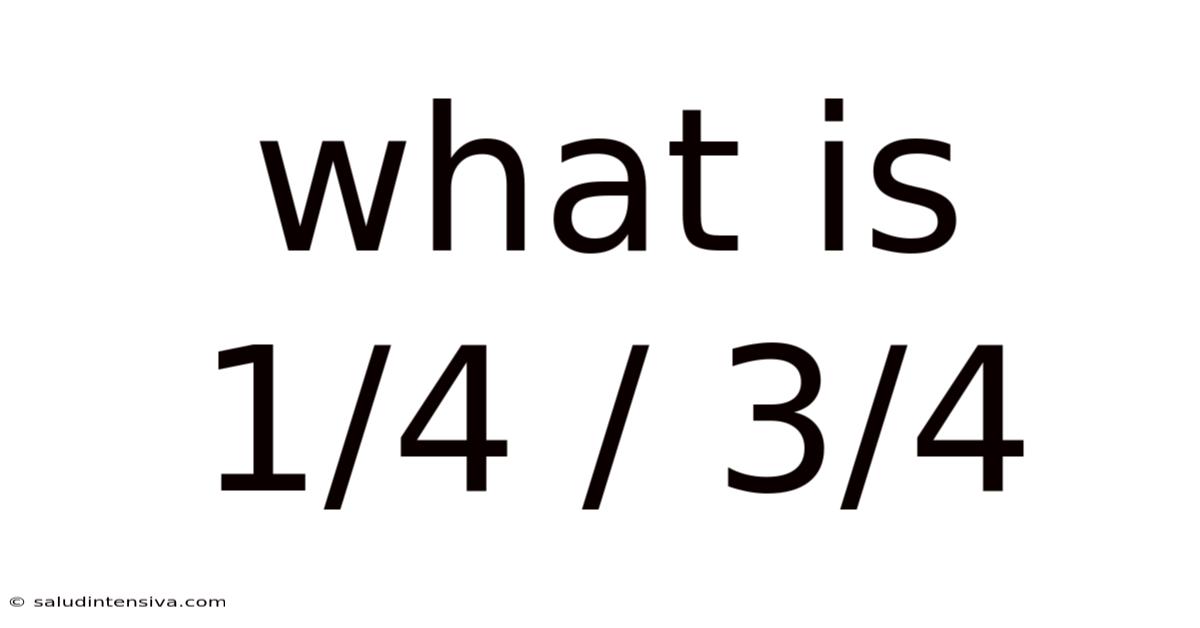
Table of Contents
Decoding the Fraction: What is 1/4 ÷ 3/4? A Comprehensive Guide
Understanding fractions and how to perform operations like division with them is a fundamental skill in mathematics. This guide will thoroughly explain how to solve the problem 1/4 ÷ 3/4, breaking down the process step-by-step and exploring the underlying mathematical concepts. We'll cover the core principles, practical applications, and frequently asked questions to ensure a complete understanding.
Introduction: Unveiling the Mystery of Fraction Division
The question, "What is 1/4 ÷ 3/4?" might seem intimidating at first glance, especially if you haven't worked with fractions in a while. However, with a clear understanding of the method, this type of problem becomes straightforward. This article aims to demystify fraction division, focusing on the specific example of 1/4 divided by 3/4, while providing a broader context for handling other fraction division problems. We will explore the concept of reciprocals, the process of inverting and multiplying, and the reasoning behind these steps.
Understanding Fractions: A Quick Refresher
Before diving into the division, let's quickly revisit the basics of fractions. A fraction represents a part of a whole. It consists of two parts:
- Numerator: The top number, indicating how many parts we have.
- Denominator: The bottom number, indicating the total number of equal parts the whole is divided into.
For example, in the fraction 1/4, the numerator is 1 and the denominator is 4. This represents one out of four equal parts.
Step-by-Step Solution: 1/4 ÷ 3/4
Dividing fractions involves a clever technique that transforms the division problem into a multiplication problem. Here's how we solve 1/4 ÷ 3/4:
Step 1: Keep the First Fraction
We keep the first fraction, 1/4, exactly as it is.
Step 2: Find the Reciprocal of the Second Fraction
The reciprocal of a fraction is obtained by swapping the numerator and denominator. The reciprocal of 3/4 is 4/3.
Step 3: Change Division to Multiplication
We replace the division sign (÷) with a multiplication sign (×).
Step 4: Multiply the Fractions
Now, we multiply the fractions:
(1/4) × (4/3) = (1 × 4) / (4 × 3) = 4/12
Step 5: Simplify the Result
The fraction 4/12 can be simplified by dividing both the numerator and denominator by their greatest common divisor, which is 4:
4/12 = (4 ÷ 4) / (12 ÷ 4) = 1/3
Therefore, 1/4 ÷ 3/4 = 1/3
The Mathematical Rationale: Why Does This Work?
The method of inverting and multiplying might seem arbitrary, but it's grounded in solid mathematical principles. Let's delve into the reasoning:
Dividing by a fraction is the same as multiplying by its reciprocal. This is because division is the inverse operation of multiplication. When we divide 'a' by 'b', we are essentially asking: "What number, when multiplied by 'b', equals 'a'?"
Consider the example: 6 ÷ 2 = 3. This means that 3 × 2 = 6.
Similarly, when we divide 1/4 by 3/4, we're asking: "What fraction, when multiplied by 3/4, equals 1/4?"
By inverting and multiplying, we're effectively finding that fraction. The process ensures we maintain the integrity of the original division problem while making it solvable using simpler multiplication rules.
Visualizing the Solution: A Real-World Analogy
Imagine you have a pizza cut into four equal slices (1/4 of a pizza). You want to divide this slice into portions that represent 3/4 of a slice. How many such portions will you get?
In essence, you are dividing 1/4 of the pizza by 3/4 of a slice. The result, 1/3, tells us that you'll have one-third of a whole pizza slice. This visual representation helps to contextualize the abstract mathematical operation.
Expanding the Concept: More Complex Fraction Division
The method of inverting and multiplying applies to any fraction division problem. For example:
5/6 ÷ 2/3 = (5/6) × (3/2) = 15/12 = 5/4
The same steps are followed: keep the first fraction, find the reciprocal of the second, change to multiplication, and simplify.
Frequently Asked Questions (FAQ)
Q1: Why do we invert the second fraction?
A1: Inverting the second fraction is crucial because division is the inverse of multiplication. By inverting and multiplying, we transform the division problem into an equivalent multiplication problem that is easier to solve.
Q2: What if the fractions are mixed numbers (e.g., 1 1/2)?
A2: First convert the mixed numbers into improper fractions. For example, 1 1/2 becomes 3/2. Then proceed with the inversion and multiplication method.
Q3: Can I simplify before multiplying?
A3: Yes! To make the multiplication simpler, you can cancel out common factors between the numerators and denominators before multiplying. This is called cross-canceling. For example, in (1/4) × (4/3), the 4 in the numerator of the second fraction and the 4 in the denominator of the first fraction cancel out, leaving (1/1) × (1/3) = 1/3.
Q4: What if the denominator of a fraction is zero?
A4: Division by zero is undefined in mathematics. You cannot divide by a fraction that has a denominator of zero.
Conclusion: Mastering Fraction Division
Understanding fraction division is essential for progressing in mathematics. The process of inverting and multiplying, while initially seeming unconventional, is a powerful technique rooted in the inverse relationship between multiplication and division. By mastering this method and understanding the underlying principles, you'll confidently tackle even more complex fraction problems. Remember the key steps: keep, change, flip, and simplify, and you'll always arrive at the correct answer. With consistent practice and a clear grasp of the concepts explained in this guide, you'll find that fraction division becomes a straightforward and manageable part of your mathematical toolkit. This fundamental skill will serve you well in various applications, from simple calculations to advanced mathematical concepts.
Latest Posts
Latest Posts
-
8 And A Half Inches
Sep 09, 2025
-
1 21 Repeating As A Fraction
Sep 09, 2025
-
What Was 12 Weeks Ago
Sep 09, 2025
-
Gcf Of 40 And 36
Sep 09, 2025
-
Lcm Of 28 And 42
Sep 09, 2025
Related Post
Thank you for visiting our website which covers about What Is 1/4 / 3/4 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.