What Is 1/4 Plus 1/8
saludintensiva
Sep 20, 2025 · 5 min read
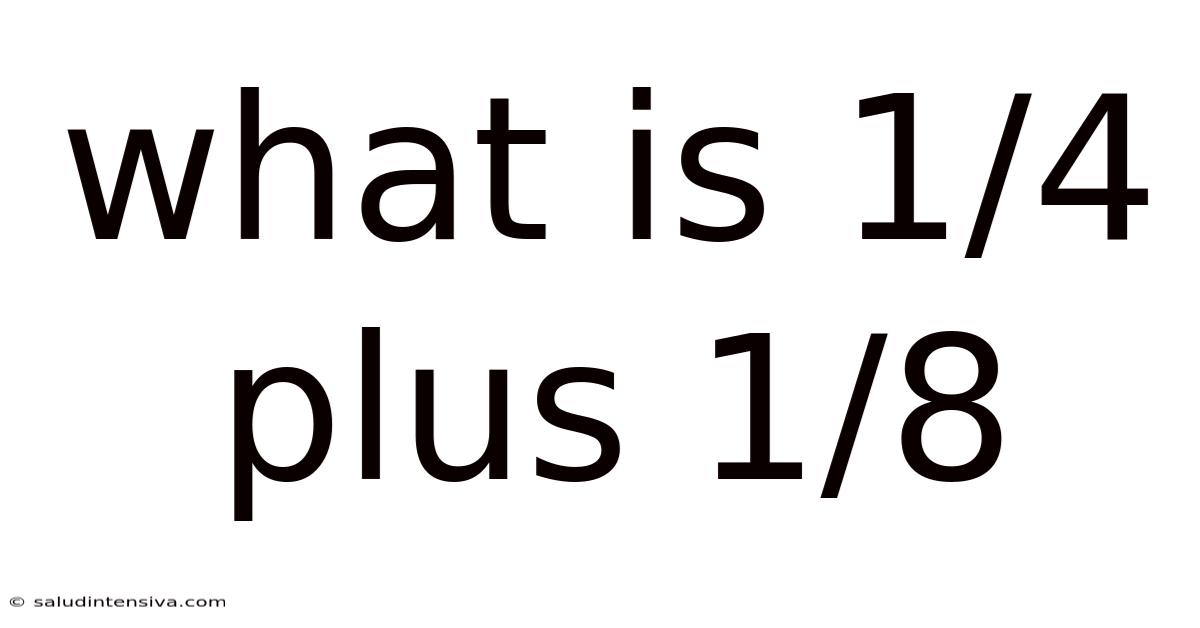
Table of Contents
What is 1/4 Plus 1/8? A Deep Dive into Fraction Addition
This article will comprehensively explain how to add the fractions 1/4 and 1/8, covering the fundamental concepts of fractions, different methods of solving the problem, and exploring related mathematical ideas. Understanding fraction addition is crucial for various mathematical applications, and this guide will empower you with a clear and thorough understanding. We'll move beyond simply providing the answer and delve into the why behind the process. This will help you confidently tackle similar problems in the future.
Introduction: Understanding Fractions
Before diving into the addition of 1/4 and 1/8, let's refresh our understanding of fractions. A fraction represents a part of a whole. It's written as a numerator (the top number) over a denominator (the bottom number), like this: numerator/denominator. The numerator indicates how many parts we have, and the denominator indicates how many equal parts the whole is divided into.
For instance, in the fraction 1/4, the numerator (1) signifies that we have one part, and the denominator (4) indicates that the whole has been divided into four equal parts. Similarly, 1/8 means we have one part out of eight equal parts.
Method 1: Finding a Common Denominator
The core principle of adding fractions is to find a common denominator. This means finding a number that is a multiple of both denominators (4 and 8, in this case). The common denominator allows us to express both fractions with the same "size" of pieces, making addition straightforward.
-
Identifying the Least Common Multiple (LCM): The most efficient common denominator is the least common multiple (LCM) of the denominators. For 4 and 8, the LCM is 8. This is because 8 is a multiple of both 4 (4 x 2 = 8) and 8 (8 x 1 = 8).
-
Converting the Fractions: Now we need to convert both fractions to have a denominator of 8. To change 1/4 to an equivalent fraction with a denominator of 8, we multiply both the numerator and the denominator by 2:
(1 x 2) / (4 x 2) = 2/8
The fraction 1/8 already has a denominator of 8, so it remains unchanged.
- Adding the Fractions: Now that both fractions have the same denominator, we can simply add the numerators:
2/8 + 1/8 = (2 + 1)/8 = 3/8
Therefore, 1/4 + 1/8 = 3/8
Method 2: Using Visual Aids
Visual representations can greatly aid understanding, especially when dealing with fractions. Let's imagine a circle representing a whole.
-
Representing 1/4: Divide the circle into four equal parts. Shade one part to represent 1/4.
-
Representing 1/8: Now, divide the same circle into eight equal parts. Shade one part to represent 1/8. You'll notice that each of the original four parts is now divided into two smaller parts.
-
Adding Visually: Observe that 1/4 is equivalent to 2/8 (two of the smaller parts). Adding the shaded parts from 1/4 (2/8) and 1/8, we have a total of three shaded parts out of eight. This visually confirms that 1/4 + 1/8 = 3/8.
Method 3: Decimal Conversion (Alternative Approach)
While not always the most efficient method for fractions, converting fractions to decimals can be useful in certain situations.
-
Converting to Decimals:
- 1/4 = 0.25 (because 1 divided by 4 is 0.25)
- 1/8 = 0.125 (because 1 divided by 8 is 0.125)
-
Adding Decimals:
- 0.25 + 0.125 = 0.375
-
Converting back to a Fraction (if needed): 0.375 can be converted back into a fraction by writing it as 375/1000. Simplifying this fraction by dividing both numerator and denominator by 125 gives us 3/8.
Explaining the Mathematical Principles: Why it Works
The success of adding fractions hinges on the concept of equivalent fractions. Equivalent fractions represent the same value but have different numerators and denominators. For example, 1/2, 2/4, 3/6, and 4/8 are all equivalent fractions. They all represent one-half of a whole.
When we find a common denominator, we are essentially converting the fractions into equivalent fractions with the same denominator. This allows us to directly add the numerators because we are then adding parts of the same size.
Frequently Asked Questions (FAQ)
-
Q: Can I add fractions with different denominators directly? A: No, you must first find a common denominator before adding fractions with different denominators.
-
Q: What if the LCM is difficult to find? A: For larger numbers, you can use the prime factorization method to find the LCM efficiently. This involves breaking down the numbers into their prime factors and then identifying the highest power of each prime factor present.
-
Q: Is there a way to simplify the answer (3/8)? A: In this case, 3/8 is already in its simplest form because 3 and 8 share no common factors other than 1.
-
Q: What if one of the fractions is a mixed number (e.g., 1 1/4)? A: First, convert the mixed number into an improper fraction (in this case, 5/4). Then, follow the steps for adding fractions with a common denominator.
Further Exploration: Extending the Concept
The principles of adding fractions extend to adding more than two fractions. You still need to find a common denominator for all the fractions involved. Furthermore, subtracting fractions follows a similar process: find a common denominator and then subtract the numerators.
Conclusion: Mastering Fraction Addition
Adding fractions, like adding 1/4 and 1/8, is a fundamental skill in mathematics. Understanding the concept of common denominators and equivalent fractions is essential for successfully solving these types of problems. Whether you prefer the method of finding the LCM, using visual aids, or even converting to decimals, the key is to ensure you have a strong grasp of the underlying mathematical principles. By mastering these concepts, you'll build a solid foundation for more advanced mathematical concepts and applications. Remember, practice is key! Work through several examples to solidify your understanding and build your confidence in adding fractions.
Latest Posts
Latest Posts
-
30 Days From June 6
Sep 21, 2025
-
1000 Cubic Inches To Liters
Sep 21, 2025
-
180 Degrees Celsius To Fahrenheit
Sep 21, 2025
-
1 3 Of 1 Million
Sep 21, 2025
-
Mach To Kilometers Per Hour
Sep 21, 2025
Related Post
Thank you for visiting our website which covers about What Is 1/4 Plus 1/8 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.