What Is 1/8 Of 1/2
saludintensiva
Sep 12, 2025 · 5 min read
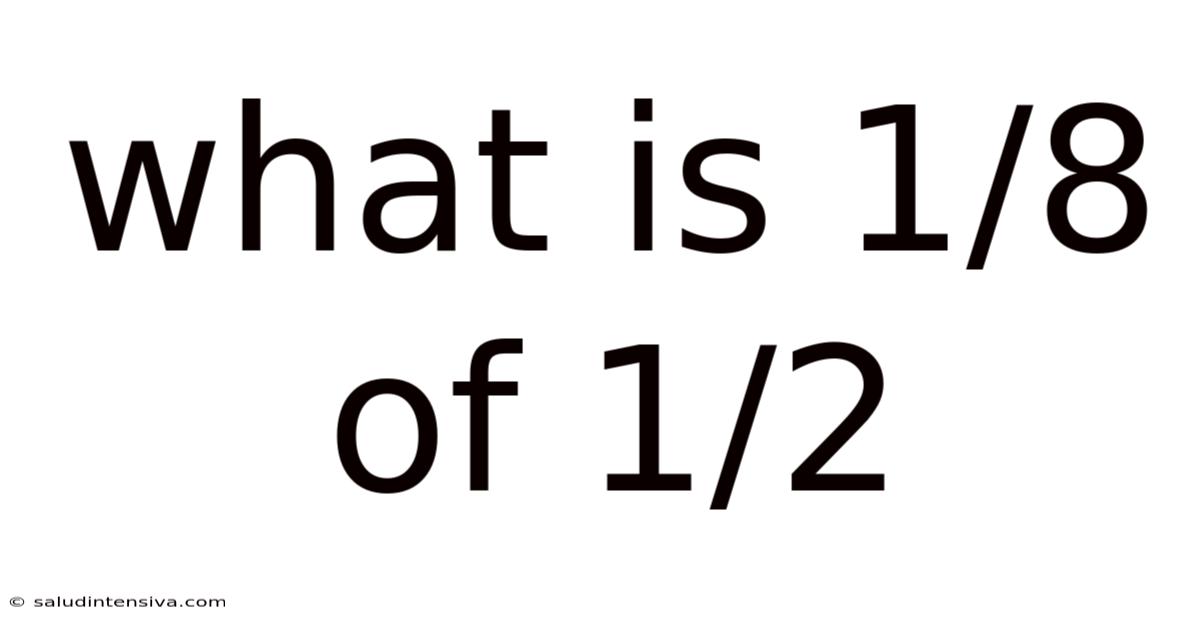
Table of Contents
What is 1/8 of 1/2? Unlocking the World of Fractions
Finding a fraction of a fraction might seem daunting at first, but it's a fundamental concept in mathematics with wide-ranging applications. This article will delve into the question, "What is 1/8 of 1/2?", providing a step-by-step explanation, exploring the underlying mathematical principles, and offering real-world examples to solidify your understanding. We'll cover various methods for solving this type of problem, ensuring you gain a comprehensive grasp of fraction manipulation.
Understanding Fractions: A Quick Refresher
Before we tackle the problem, let's briefly revisit the basics of fractions. A fraction represents a part of a whole. It's expressed as a ratio of two numbers: the numerator (top number) and the denominator (bottom number). The numerator indicates how many parts you have, while the denominator indicates how many parts make up the whole. For example, in the fraction 1/2, the numerator is 1 and the denominator is 2, representing one of two equal parts.
Method 1: Multiplying Fractions
The most straightforward way to find a fraction of another fraction is to multiply them. To multiply fractions, you simply multiply the numerators together and the denominators together. In our case:
1/8 of 1/2 can be written as: (1/8) x (1/2)
Multiply the numerators: 1 x 1 = 1
Multiply the denominators: 8 x 2 = 16
Therefore, 1/8 of 1/2 = 1/16
This method is efficient and easily applicable to various fraction problems.
Method 2: Visual Representation
Visual aids can significantly enhance understanding, especially when dealing with abstract concepts like fractions. Imagine a rectangular pizza cut into 8 equal slices. 1/8 of the pizza represents one of these slices. Now, let's consider only half (1/2) of the pizza. We are interested in finding 1/8 of this half.
If you take half the pizza (4 slices), and then divide that half into 8 equal parts, each of those smaller parts represents 1/16 of the original pizza. This visual representation clearly shows that 1/8 of 1/2 is indeed 1/16.
This method is particularly useful for beginners as it provides a concrete representation of the abstract mathematical operation.
Method 3: Converting to Decimals (Alternative Approach)
While not strictly necessary, converting fractions to decimals can offer an alternative approach, especially for those more comfortable with decimal calculations.
- Convert the fractions to decimals: 1/8 = 0.125 and 1/2 = 0.5
- Multiply the decimals: 0.125 x 0.5 = 0.0625
- Convert the decimal back to a fraction: 0.0625 = 625/10000
- Simplify the fraction: 625/10000 simplifies to 1/16 by dividing both numerator and denominator by 625.
While this method works, it adds an extra step and might be less efficient than direct fraction multiplication, especially when dealing with more complex fractions.
Expanding the Understanding: Working with More Complex Fractions
The principles discussed above can be extended to more complex fraction problems. Let's explore a few examples:
- Finding 2/3 of 3/4: (2/3) x (3/4) = (2 x 3) / (3 x 4) = 6/12 = 1/2
- Finding 5/6 of 2/5: (5/6) x (2/5) = (5 x 2) / (6 x 5) = 10/30 = 1/3
Notice that in these examples, we can often simplify the resulting fractions. This simplification makes the answer easier to understand and interpret. Always simplify your fractions to their lowest terms. For instance, 6/12 can be simplified to 1/2 by dividing both the numerator and denominator by their greatest common divisor, which is 6.
Real-World Applications
The ability to calculate fractions of fractions is crucial in various real-world scenarios:
- Cooking: A recipe calls for 1/2 cup of flour, but you only want to make 1/4 of the recipe. How much flour do you need? (1/4) x (1/2) = 1/8 cup of flour.
- Construction: A project requires 1/2 a yard of lumber, and you need 1/3 of that amount. How much lumber do you need? (1/3) x (1/2) = 1/6 yard of lumber.
- Finance: If you invest 1/4 of your savings and then spend 1/5 of that investment, what fraction of your total savings did you spend? (1/5) x (1/4) = 1/20 of your savings.
These examples demonstrate the practical application of fraction multiplication in everyday situations. Understanding this concept is essential for effective problem-solving across many disciplines.
Frequently Asked Questions (FAQ)
Q: What if the fractions are mixed numbers (e.g., 1 1/2)?
A: Before multiplying, you need to convert mixed numbers into improper fractions. For example, 1 1/2 converts to 3/2. Then, proceed with the multiplication as described earlier.
Q: Can I use a calculator to solve fraction problems?
A: Yes, most calculators have fraction capabilities. However, understanding the underlying principles is crucial even if you utilize a calculator.
Q: Why is simplification of fractions important?
A: Simplification makes the result easier to understand and interpret. It also ensures that the answer is in its most concise form.
Q: Are there other methods to solve fraction problems besides multiplication?
A: While multiplication is the most direct approach, you could potentially use visual aids or repeated subtraction for simpler problems, but multiplication offers a more efficient and universally applicable solution.
Conclusion: Mastering Fractions for a Brighter Future
Understanding how to find a fraction of a fraction, as demonstrated through the problem "What is 1/8 of 1/2?", is a fundamental building block in mathematics. The ability to confidently manipulate fractions opens doors to solving complex problems in various fields, from cooking and construction to finance and beyond. By mastering this seemingly simple concept, you equip yourself with a valuable tool for navigating the quantitative aspects of the world around you. Remember the three primary methods: direct multiplication, visual representation, and (less efficiently) decimal conversion. Practice consistently and don't hesitate to revisit the basic principles of fractions if needed. The journey to mastering fractions is rewarding, and the skills you acquire will undoubtedly serve you well throughout your life.
Latest Posts
Latest Posts
-
How To Find Avg Velocity
Sep 13, 2025
-
29 30 As A Decimal
Sep 13, 2025
-
Gcf For 12 And 48
Sep 13, 2025
-
10 To The 6th Power
Sep 13, 2025
-
Lcm For 16 And 20
Sep 13, 2025
Related Post
Thank you for visiting our website which covers about What Is 1/8 Of 1/2 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.