What Is 10 Of 25
saludintensiva
Sep 14, 2025 · 5 min read
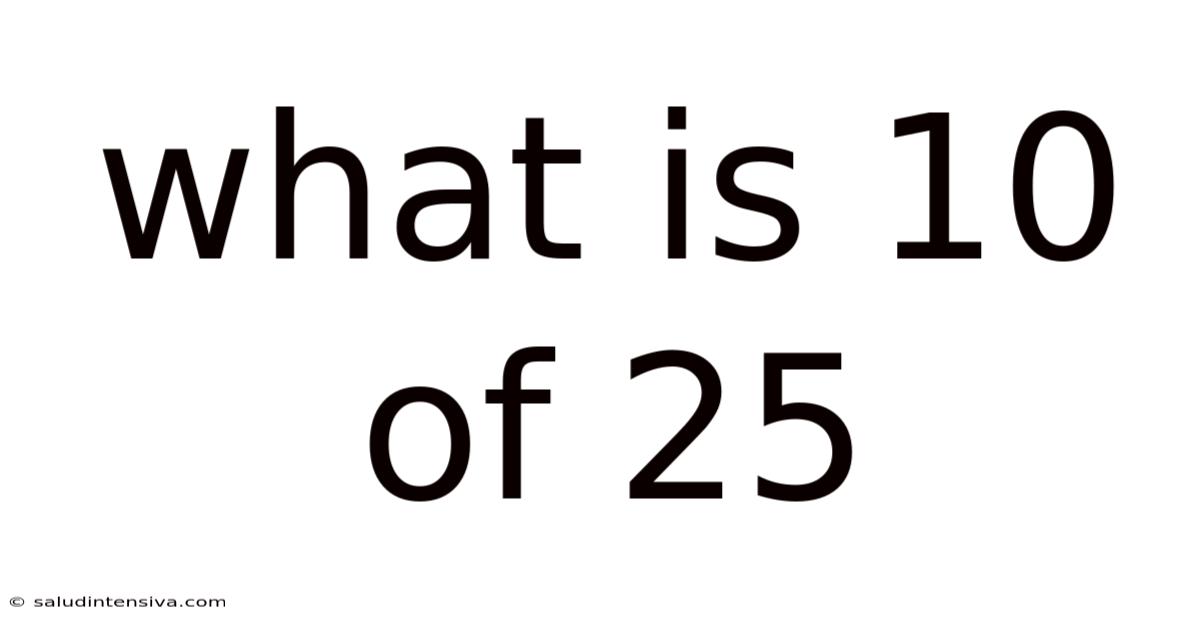
Table of Contents
What is 10 of 25? Deconstructing Fractions, Percentages, and Ratios
This article explores the seemingly simple question, "What is 10 of 25?", delving far beyond a simple numerical answer. We'll dissect this problem, revealing the underlying mathematical concepts of fractions, percentages, and ratios, and showing how they interconnect and apply to various real-world scenarios. Understanding these concepts is crucial for everyday life, from calculating discounts to understanding financial reports. This comprehensive guide will equip you with the knowledge to confidently tackle similar problems and build a stronger foundation in mathematics.
Understanding the Core Concept: Fractions
At its heart, "10 of 25" represents a fraction. A fraction is a part of a whole, expressed as a ratio of two numbers – the numerator (top number) and the denominator (bottom number). In this case, 10 is the numerator, representing the part we're interested in, and 25 is the denominator, representing the whole. Therefore, "10 of 25" can be written as the fraction 10/25.
Simplifying Fractions: The fraction 10/25 isn't in its simplest form. To simplify a fraction, we find the greatest common divisor (GCD) of both the numerator and the denominator and divide both by it. The GCD of 10 and 25 is 5. Dividing both the numerator and the denominator by 5, we get:
10 ÷ 5 / 25 ÷ 5 = 2/5
This means that 10 out of 25 is equivalent to 2 out of 5. This simplified fraction is easier to understand and work with.
Converting Fractions to Percentages
Percentages are another way of expressing parts of a whole. A percentage represents a fraction where the denominator is 100. To convert a fraction to a percentage, we divide the numerator by the denominator and multiply the result by 100%.
Using our simplified fraction 2/5:
(2 ÷ 5) x 100% = 0.4 x 100% = 40%
Therefore, 10 out of 25 is equal to 40%. This means that 10 represents 40% of the total 25.
Exploring Ratios
A ratio is a comparison of two or more quantities. In our case, the ratio of 10 to 25 can be written as 10:25 or 10/25. Similar to fractions, ratios can be simplified by dividing both parts by their GCD (5 in this case), resulting in the simplified ratio 2:5. This signifies that for every 2 units of one quantity, there are 5 units of the other.
Ratios are frequently used in various fields:
- Cooking: A recipe might call for a 2:1 ratio of flour to sugar.
- Maps: Maps use ratios (scales) to represent distances on the ground.
- Mixing: Painters use ratios to mix colors to achieve desired shades.
Real-World Applications of 10 out of 25
Understanding how to work with fractions, percentages, and ratios is essential for various real-world scenarios. Here are some examples:
-
Test Scores: Imagine a student scoring 10 out of 25 on a quiz. Their score is 40%, indicating they answered 40% of the questions correctly. This helps assess their understanding of the subject matter.
-
Sales and Discounts: A store offering a discount of 10 items out of a total of 25 items is effectively offering a 40% discount on a selection of their inventory.
-
Inventory Management: A warehouse manager might track inventory levels by comparing the number of items sold (10) to the total number of items available (25), which shows they’ve sold 40% of their stock.
-
Probability: If there are 25 balls in a bag, 10 of which are red, the probability of picking a red ball at random is 10/25 or 2/5, which is 40%.
-
Data Analysis: In data analysis, ratios and percentages are used extensively to represent proportions and trends within datasets. For instance, 10 out of 25 customers choosing a specific product demonstrates a 40% preference for that particular item.
Further Mathematical Explorations
The simple problem "What is 10 of 25?" opens doors to further mathematical exploration:
-
Proportions: The concept of proportion is closely related to fractions and ratios. A proportion is an equation stating that two ratios are equal. For example, 10/25 = 2/5 is a proportion. Solving proportions is a key skill in many mathematical applications.
-
Decimals: Fractions can be easily converted to decimals by performing the division indicated by the fraction. In our case, 10/25 or 2/5 equals 0.4. Decimals are essential for calculations and data representation.
-
Algebra: Algebraic equations often involve fractions and ratios. Solving these equations often requires understanding how to manipulate fractions and ratios.
Frequently Asked Questions (FAQ)
Q: Can I use a calculator to solve this?
A: Yes, absolutely. A calculator can quickly convert fractions to decimals and percentages. However, understanding the underlying mathematical principles is crucial for applying these concepts in various contexts.
Q: What if the numbers were larger?
A: The same principles apply. You would still simplify the fraction, convert it to a percentage, and consider its ratio representation. Larger numbers might require a calculator for efficient calculations.
Q: Are there other ways to represent 10 out of 25?
A: Yes, as demonstrated, you can represent it as a fraction (10/25 or its simplified form 2/5), a percentage (40%), a decimal (0.4), and a ratio (10:25 or 2:5).
Q: Why is simplifying fractions important?
A: Simplifying fractions makes them easier to understand and work with. It also helps in comparing fractions more easily. A simplified fraction represents the same value but in a more concise form.
Conclusion
The seemingly simple question, "What is 10 of 25?", unveils a rich tapestry of mathematical concepts. We’ve explored the interconnectedness of fractions, percentages, and ratios, demonstrating their practical applications in everyday life and various professional fields. Mastering these fundamental concepts provides a strong foundation for further mathematical learning and empowers you to tackle complex problems with confidence. Remember that while calculators can assist with calculations, a solid grasp of the underlying principles remains crucial for problem-solving and critical thinking. By understanding the relationships between fractions, percentages, and ratios, you can confidently interpret and utilize numerical data in any situation you encounter.
Latest Posts
Latest Posts
-
What Are Multiples Of 12
Sep 14, 2025
-
How Long Is 228 Minutes
Sep 14, 2025
-
1 7 M Height In Feet
Sep 14, 2025
-
Is 3 8 Or 5 8 Bigger
Sep 14, 2025
-
L 64 Meter In Feet
Sep 14, 2025
Related Post
Thank you for visiting our website which covers about What Is 10 Of 25 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.