What Is 12 5 Simplified
saludintensiva
Sep 12, 2025 · 5 min read
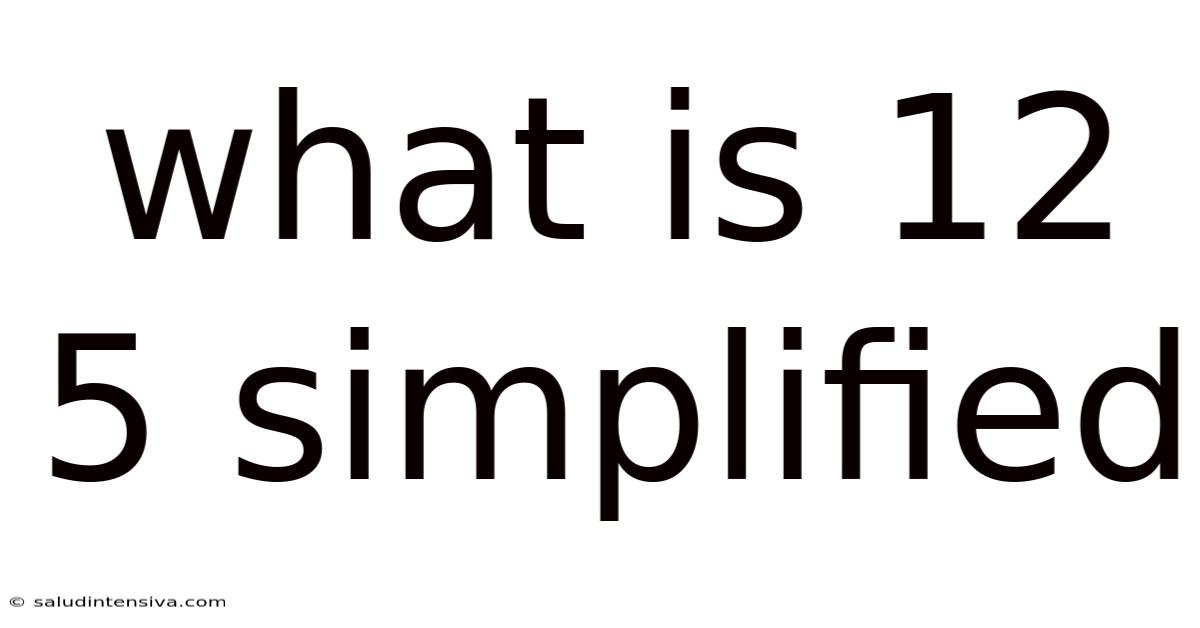
Table of Contents
What is 12/5 Simplified? Understanding Fractions and Their Simplification
Understanding fractions is fundamental to mathematics and numerous real-world applications. This article delves into the simplification of fractions, specifically addressing the question: What is 12/5 simplified? We'll explore the concept of simplifying fractions, the steps involved, and provide a clear explanation that caters to all levels of mathematical understanding. We'll also touch upon related concepts and answer frequently asked questions.
Introduction to Fractions
A fraction represents a part of a whole. It's expressed as a ratio of two numbers: the numerator (the top number) and the denominator (the bottom number). The denominator indicates how many equal parts the whole is divided into, while the numerator indicates how many of those parts are being considered. For example, in the fraction 12/5, 12 is the numerator and 5 is the denominator. This means we have 12 parts out of a whole that's divided into 5 equal parts.
Simplifying Fractions: The Concept of Greatest Common Divisor (GCD)
Simplifying a fraction means expressing it in its lowest terms. This involves reducing the numerator and the denominator to their smallest possible whole numbers while maintaining the fraction's value. The key to simplification lies in finding the Greatest Common Divisor (GCD), also known as the Greatest Common Factor (GCF), of both the numerator and the denominator. The GCD is the largest number that divides both the numerator and the denominator without leaving a remainder.
Finding the GCD: Methods and Examples
Several methods exist for finding the GCD. Let's explore two common approaches:
1. Listing Factors: This method involves listing all the factors (numbers that divide evenly) of both the numerator and the denominator. Then, identify the largest factor common to both lists.
-
Example: Let's find the GCD of 12 and 5.
- Factors of 12: 1, 2, 3, 4, 6, 12
- Factors of 5: 1, 5
The largest common factor is 1.
2. Prime Factorization: This method involves expressing both the numerator and the denominator as a product of their prime factors (numbers divisible only by 1 and themselves). The GCD is then the product of the common prime factors raised to the lowest power.
-
Example: Let's find the GCD of 12 and 5 using prime factorization.
- Prime factorization of 12: 2 x 2 x 3 = 2² x 3
- Prime factorization of 5: 5 (5 is a prime number)
There are no common prime factors between 12 and 5. Therefore, the GCD is 1.
Simplifying 12/5
Since the GCD of 12 and 5 is 1, we can't simplify 12/5 further by dividing both the numerator and denominator by a common factor greater than 1. Therefore, 12/5 is already in its simplest form.
Converting Improper Fractions to Mixed Numbers
While 12/5 is simplified, it's an improper fraction because the numerator (12) is larger than the denominator (5). Improper fractions are often converted to mixed numbers, which consist of a whole number and a proper fraction (where the numerator is smaller than the denominator).
To convert 12/5 to a mixed number, we perform division:
12 ÷ 5 = 2 with a remainder of 2.
This means that 12/5 can be expressed as 2 2/5. This represents 2 whole units and 2/5 of another unit.
Understanding the Significance of Simplification
Simplifying fractions is crucial for several reasons:
- Clarity: Simplified fractions are easier to understand and interpret than their unsimplified counterparts.
- Efficiency: Simplified fractions make calculations simpler and more efficient.
- Standardization: Expressing fractions in their simplest form ensures consistency and avoids ambiguity.
- Comparison: Simplified fractions facilitate easier comparison of different fractions.
Practical Applications of Fractions and Simplification
Fractions and their simplification are fundamental to many areas:
- Cooking and Baking: Following recipes often involves working with fractions of ingredients.
- Construction and Engineering: Precise measurements and calculations frequently require the use of fractions.
- Finance: Working with percentages, interest rates, and financial ratios involves fractions.
- Science: Scientific measurements and calculations often use fractions to express precise quantities.
Frequently Asked Questions (FAQ)
Q: Can all fractions be simplified?
A: No, some fractions, like 12/5 (as shown above) and others where the GCD is 1, are already in their simplest form and cannot be simplified further.
Q: What if the GCD is the numerator or denominator itself?
A: If the GCD is equal to the numerator, the simplified fraction will be a whole number (numerator/GCD). If the GCD is equal to the denominator, the simplified fraction will be 0 (numerator/GCD = 0).
Q: Is there a shortcut for finding the GCD of larger numbers?
A: Yes, the Euclidean algorithm is a more efficient method for finding the GCD of larger numbers than listing factors or prime factorization, especially when dealing with large numbers.
Q: How do I simplify fractions with negative numbers?
A: Simplify the fraction as you normally would, ignoring the negative sign. Then, apply the negative sign to the simplified fraction. For example, -12/5 simplifies to -2 2/5.
Q: Why is it important to learn about simplifying fractions?
A: Simplifying fractions makes working with fractions easier and more efficient in many situations. It also helps us to better understand and represent quantities in their simplest form. It improves our mathematical literacy and strengthens our problem-solving skills across various applications.
Conclusion: Mastering Fraction Simplification
Simplifying fractions is a core skill in mathematics, enabling clearer understanding, more efficient calculations, and easier problem-solving. While 12/5 cannot be simplified further in the traditional sense, understanding its conversion to a mixed number (2 2/5) is crucial. This detailed exploration of fraction simplification has not only answered the question "What is 12/5 simplified?" but also equipped you with the knowledge and methods to tackle similar problems confidently. Remember to practice regularly to master this fundamental mathematical concept and appreciate its widespread applications in various fields. The understanding of GCD and its different methods of calculation is pivotal for approaching more complex fraction simplification tasks. Continue practicing and exploring different approaches to solidify your understanding of this essential mathematical concept.
Latest Posts
Latest Posts
-
Gcf Of 56 And 72
Sep 12, 2025
-
Is 25 Prime Or Composite
Sep 12, 2025
-
Equivalent Fractions For 3 6
Sep 12, 2025
-
Discount Tax And Tip Calculator
Sep 12, 2025
-
90 Days From July 1
Sep 12, 2025
Related Post
Thank you for visiting our website which covers about What Is 12 5 Simplified . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.