What Is 12 9 Simplified
saludintensiva
Sep 18, 2025 · 6 min read
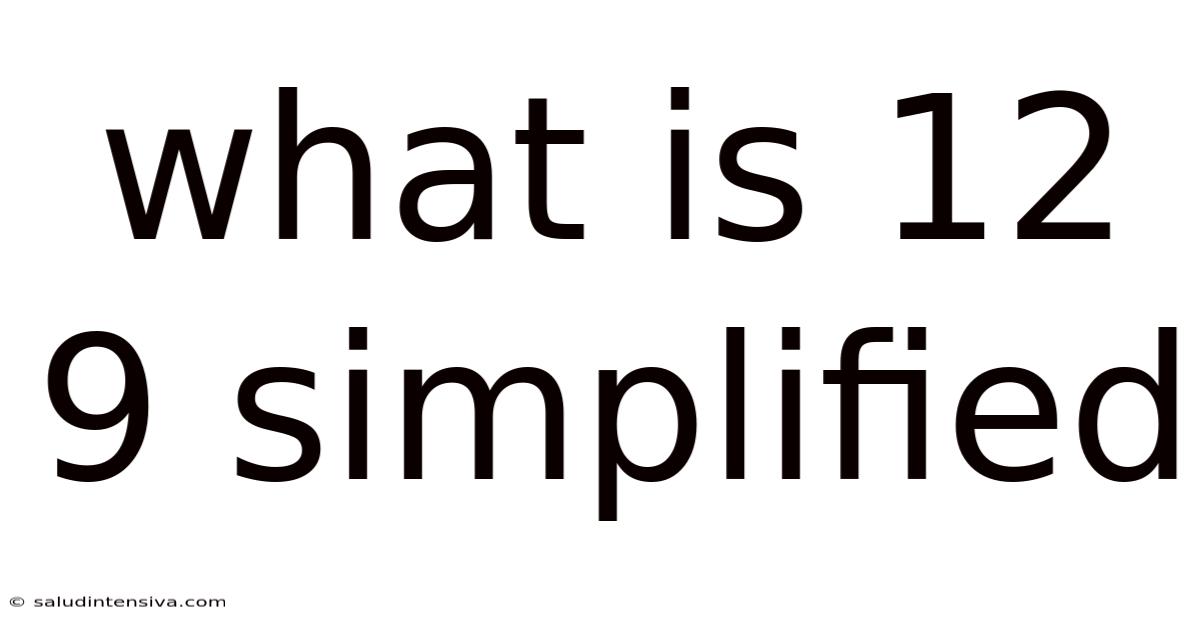
Table of Contents
What is 12/9 Simplified? Understanding Fractions and Simplification
The question "What is 12/9 simplified?" seems simple, but it touches upon fundamental concepts in mathematics, specifically fractions and their simplification. Understanding how to simplify fractions isn't just about getting the right answer; it's about grasping the underlying principles of equivalent fractions and working towards mathematical fluency. This article will comprehensively explore the simplification of 12/9, providing a step-by-step explanation, addressing common misconceptions, and delving into the broader mathematical context.
Introduction to Fractions
Before we tackle the simplification of 12/9, let's briefly review the basics of fractions. A fraction represents a part of a whole. It's written in the form a/b, where:
- a is the numerator, representing the number of parts we have.
- b is the denominator, representing the total number of equal parts the whole is divided into.
For example, in the fraction 3/4, the numerator (3) signifies that we have 3 parts, and the denominator (4) indicates that the whole is divided into 4 equal parts.
Understanding Equivalent Fractions
Equivalent fractions represent the same proportion or value, even though they look different. For instance, 1/2, 2/4, 3/6, and 4/8 are all equivalent fractions. They all represent exactly half of a whole. We can obtain equivalent fractions by multiplying or dividing both the numerator and the denominator by the same non-zero number. This is crucial for simplifying fractions.
Simplifying Fractions: The Process
Simplifying a fraction means reducing it to its lowest terms. This means finding an equivalent fraction where the numerator and the denominator have no common factors other than 1. The process involves finding the greatest common divisor (GCD) of the numerator and denominator and then dividing both by the GCD.
Step-by-Step Simplification of 12/9
Let's apply this process to simplify 12/9:
-
Find the Greatest Common Divisor (GCD): The GCD is the largest number that divides both the numerator (12) and the denominator (9) without leaving a remainder. We can find the GCD using several methods:
-
Listing Factors: List the factors of 12 (1, 2, 3, 4, 6, 12) and the factors of 9 (1, 3, 9). The greatest common factor is 3.
-
Prime Factorization: Express both numbers as a product of prime numbers:
- 12 = 2 x 2 x 3
- 9 = 3 x 3 The common prime factor is 3. Therefore, the GCD is 3.
-
Euclidean Algorithm: This is a more efficient method for larger numbers. It involves repeatedly applying the division algorithm until the remainder is 0. The last non-zero remainder is the GCD.
- 12 ÷ 9 = 1 with a remainder of 3
- 9 ÷ 3 = 3 with a remainder of 0 The GCD is 3.
-
-
Divide the Numerator and Denominator by the GCD: Now that we've found the GCD (3), we divide both the numerator and the denominator of 12/9 by 3:
- 12 ÷ 3 = 4
- 9 ÷ 3 = 3
-
Simplified Fraction: The simplified fraction is 4/3.
Therefore, 12/9 simplified is 4/3.
Improper Fractions and Mixed Numbers
Notice that 4/3 is an improper fraction, meaning the numerator (4) is larger than the denominator (3). Improper fractions can be converted into mixed numbers, which combine a whole number and a proper fraction. To convert 4/3 to a mixed number:
-
Divide the numerator by the denominator: 4 ÷ 3 = 1 with a remainder of 1.
-
Write the result as a mixed number: The quotient (1) becomes the whole number, and the remainder (1) becomes the numerator of the fraction, while the denominator remains the same (3). Therefore, 4/3 is equivalent to 1 1/3.
Visual Representation
Visualizing fractions can help solidify understanding. Imagine a pizza cut into 9 slices. 12/9 means you have 12 slices of that pizza. Since each pizza only has 9 slices, you actually have one whole pizza (9/9) and 3 more slices (3/9), which simplifies to 1 1/3 pizzas.
Common Mistakes and Misconceptions
-
Incorrect GCD: Failing to find the greatest common divisor will result in an incomplete simplification. For example, if you only divide 12/9 by 2, you get 6/4.5, which is still not simplified.
-
Dividing only the numerator or denominator: Remember that you must divide both the numerator and the denominator by the GCD to maintain the equivalent fraction.
-
Not converting improper fractions: Leaving the answer as an improper fraction (4/3) is acceptable in many contexts, but converting it to a mixed number (1 1/3) can be more intuitive in some applications.
Further Applications and Extensions
Understanding fraction simplification is crucial for various mathematical operations, including:
-
Adding and Subtracting Fractions: Before you can add or subtract fractions, you usually need to find a common denominator. Simplifying fractions helps simplify this process.
-
Multiplying and Dividing Fractions: Simplifying fractions before performing these operations can make the calculations easier and result in a simpler final answer.
-
Solving Equations: Simplifying fractions is often a necessary step in solving equations involving fractions.
-
Real-world applications: Fractions are used extensively in everyday life, such as in cooking, construction, and finance. Understanding how to simplify them is essential for accurate calculations in these areas.
Frequently Asked Questions (FAQ)
-
Q: Can I simplify a fraction by dividing the numerator and denominator by different numbers? *A: No, this will change the value of the fraction. You must divide both the numerator and the denominator by the same number.
-
Q: What if the GCD is 1? *A: If the GCD is 1, the fraction is already in its simplest form. It cannot be simplified further.
-
Q: Is it always necessary to convert an improper fraction to a mixed number? *A: Not always. Improper fractions are perfectly valid representations. However, in some contexts, mixed numbers might be more practical or easier to understand.
-
Q: Are there online tools to help simplify fractions? *A: Yes, many websites and calculators are available to help simplify fractions automatically. However, understanding the underlying principles is still crucial for developing mathematical proficiency.
Conclusion
Simplifying 12/9 to 4/3, or equivalently 1 1/3, is a fundamental skill in mathematics. This seemingly simple task highlights core concepts like equivalent fractions, the greatest common divisor, and the difference between improper fractions and mixed numbers. Mastering fraction simplification isn't merely about obtaining the correct answer; it’s about building a solid foundation for more advanced mathematical concepts and problem-solving. By understanding the process and addressing common misconceptions, you can confidently tackle similar problems and develop a deeper appreciation for the beauty and logic of mathematics. Remember, consistent practice and a clear understanding of the underlying principles are key to mastering this essential skill.
Latest Posts
Latest Posts
-
Lcm Of 12 And 40
Sep 18, 2025
-
5 1 2 Improper Fraction
Sep 18, 2025
-
5 Converted To A Fraction
Sep 18, 2025
-
64 Sq Meters To Feet
Sep 18, 2025
-
10 6 In Simplest Form
Sep 18, 2025
Related Post
Thank you for visiting our website which covers about What Is 12 9 Simplified . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.