What Is 2/3 Minus 1/2
saludintensiva
Sep 21, 2025 · 6 min read
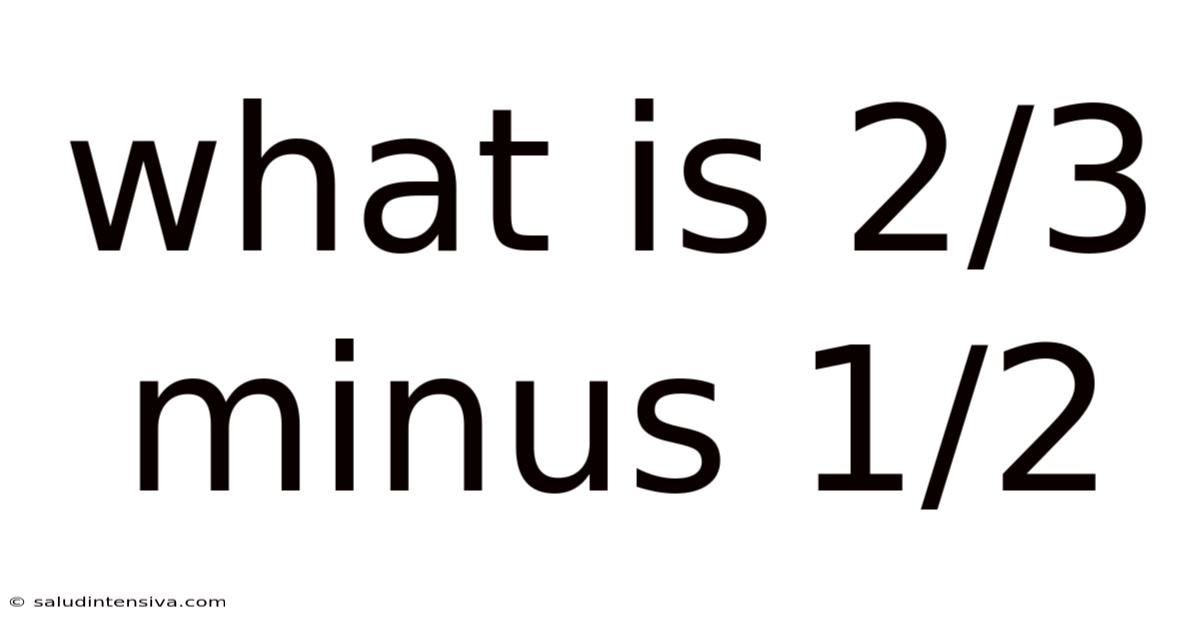
Table of Contents
What is 2/3 Minus 1/2? A Deep Dive into Fraction Subtraction
This article will explore the seemingly simple question: what is 2/3 minus 1/2? While the answer itself is straightforward, the process of solving it unlocks a deeper understanding of fractions, a fundamental concept in mathematics. We'll delve into the step-by-step solution, explain the underlying principles, and address common misconceptions surrounding fraction subtraction. By the end, you’ll not only know the answer but also possess a solid grasp of the methodology applicable to a wide range of fraction problems.
Understanding Fractions: A Quick Recap
Before we tackle the subtraction, let's refresh our understanding of fractions. A fraction represents a part of a whole. It's written as a numerator (the top number) over a denominator (the bottom number). The numerator indicates how many parts we have, while the denominator shows how many equal parts the whole is divided into. For example, in the fraction 2/3, the numerator (2) tells us we have two parts, and the denominator (3) tells us the whole is divided into three equal parts.
Crucially, to perform operations like addition and subtraction on fractions, they must have a common denominator. This is because you can only directly add or subtract parts of the same size.
Step-by-Step Solution: 2/3 - 1/2
Here's how to solve 2/3 - 1/2:
1. Find the Least Common Denominator (LCD):
The first step is to find the least common denominator (LCD) for 3 and 2. The LCD is the smallest number that is a multiple of both denominators. In this case, the multiples of 3 are 3, 6, 9, 12… and the multiples of 2 are 2, 4, 6, 8… The smallest number they have in common is 6. Therefore, our LCD is 6.
2. Convert Fractions to Equivalent Fractions with the LCD:
Now, we need to convert both fractions to equivalent fractions with a denominator of 6. To do this, we multiply both the numerator and the denominator of each fraction by the number needed to obtain the LCD:
-
For 2/3: We need to multiply both the numerator and denominator by 2 (because 3 x 2 = 6): (2 x 2) / (3 x 2) = 4/6
-
For 1/2: We need to multiply both the numerator and denominator by 3 (because 2 x 3 = 6): (1 x 3) / (2 x 3) = 3/6
3. Subtract the Numerators:
Now that both fractions have the same denominator, we can subtract the numerators:
4/6 - 3/6 = (4 - 3) / 6 = 1/6
Therefore, 2/3 - 1/2 = 1/6
Visualizing Fraction Subtraction
Visual aids can greatly enhance understanding. Imagine a circle divided into six equal parts. 2/3 represents four of these parts (4/6), and 1/2 represents three of these parts (3/6). Subtracting 1/2 (3/6) from 2/3 (4/6) leaves us with one part out of six, which is 1/6. This visual representation reinforces the mathematical process.
The Importance of the Common Denominator
The common denominator is crucial because it ensures we are comparing and subtracting like quantities. Imagine trying to subtract apples from oranges – it doesn't make sense unless you convert them to a common unit. Similarly, you can't directly subtract thirds from halves; you must first convert them to a common unit, in this case, sixths.
Working with Larger Fractions and Mixed Numbers
The same principles apply to more complex fraction subtraction problems involving larger numbers or mixed numbers (numbers with a whole number part and a fraction part). Let’s consider an example with mixed numbers:
Example: 3 1/4 - 1 2/3
1. Convert Mixed Numbers to Improper Fractions:
First, convert the mixed numbers into improper fractions. An improper fraction has a numerator larger than or equal to its denominator.
- 3 1/4 = (3 x 4 + 1) / 4 = 13/4
- 1 2/3 = (1 x 3 + 2) / 3 = 5/3
2. Find the LCD:
The LCD of 4 and 3 is 12.
3. Convert to Equivalent Fractions:
- 13/4 = (13 x 3) / (4 x 3) = 39/12
- 5/3 = (5 x 4) / (3 x 4) = 20/12
4. Subtract:
39/12 - 20/12 = (39 - 20) / 12 = 19/12
5. Convert back to a Mixed Number (if necessary):
Since 19/12 is an improper fraction, convert it back to a mixed number: 19 divided by 12 is 1 with a remainder of 7, so the answer is 1 7/12.
Therefore, 3 1/4 - 1 2/3 = 1 7/12
Addressing Common Mistakes
Several common mistakes can occur when subtracting fractions. Let's address a few:
- Forgetting to find the LCD: This is the most frequent error. Always ensure the fractions have a common denominator before subtracting the numerators.
- Incorrectly converting fractions: Pay close attention to the multiplication when converting fractions to equivalent fractions. Remember to multiply both the numerator and the denominator by the same number.
- Subtracting denominators: The denominators remain the same; only the numerators are subtracted.
- Simplifying incorrectly: After subtraction, always simplify the resulting fraction to its lowest terms if possible. For example, 2/4 should be simplified to 1/2.
Frequently Asked Questions (FAQ)
-
Q: Can I subtract fractions with different denominators directly?
- A: No, you must first find the least common denominator (LCD) and convert the fractions to equivalent fractions with that LCD before subtracting.
-
Q: What if the result is an improper fraction?
- A: Convert the improper fraction to a mixed number to express it in a more understandable format.
-
Q: How do I simplify a fraction?
- A: Find the greatest common divisor (GCD) of the numerator and denominator, and divide both by the GCD.
-
Q: What if I have more than two fractions to subtract?
- A: Find the LCD of all the denominators, convert all fractions to equivalent fractions with that LCD, and then subtract the numerators sequentially.
-
Q: Are there any online calculators or tools to help with fraction subtraction?
- A: Yes, many online calculators are available that can perform fraction calculations. However, understanding the underlying process is crucial for developing mathematical proficiency.
Conclusion: Mastering Fraction Subtraction
Subtracting fractions, although initially appearing simple, involves a systematic approach that builds upon foundational mathematical concepts. Mastering fraction subtraction requires a thorough understanding of fractions, the concept of a common denominator, and the ability to manipulate fractions correctly. By following the steps outlined above and practicing regularly, you'll build confidence and proficiency in tackling more complex fraction problems. Remember, the key is to break down the problem into manageable steps and pay careful attention to detail. With consistent practice, fraction subtraction will become second nature, empowering you to tackle more advanced mathematical challenges with ease.
Latest Posts
Latest Posts
-
How Big Is 250 Acres
Sep 21, 2025
-
What Is A Fractional Notation
Sep 21, 2025
-
What Is Nvm In Text
Sep 21, 2025
-
Convert 7 5 Inches To Centimeters
Sep 21, 2025
-
1 3 Fraction To Decimal
Sep 21, 2025
Related Post
Thank you for visiting our website which covers about What Is 2/3 Minus 1/2 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.