What Is 2/3 Times 1/2
saludintensiva
Sep 19, 2025 · 5 min read
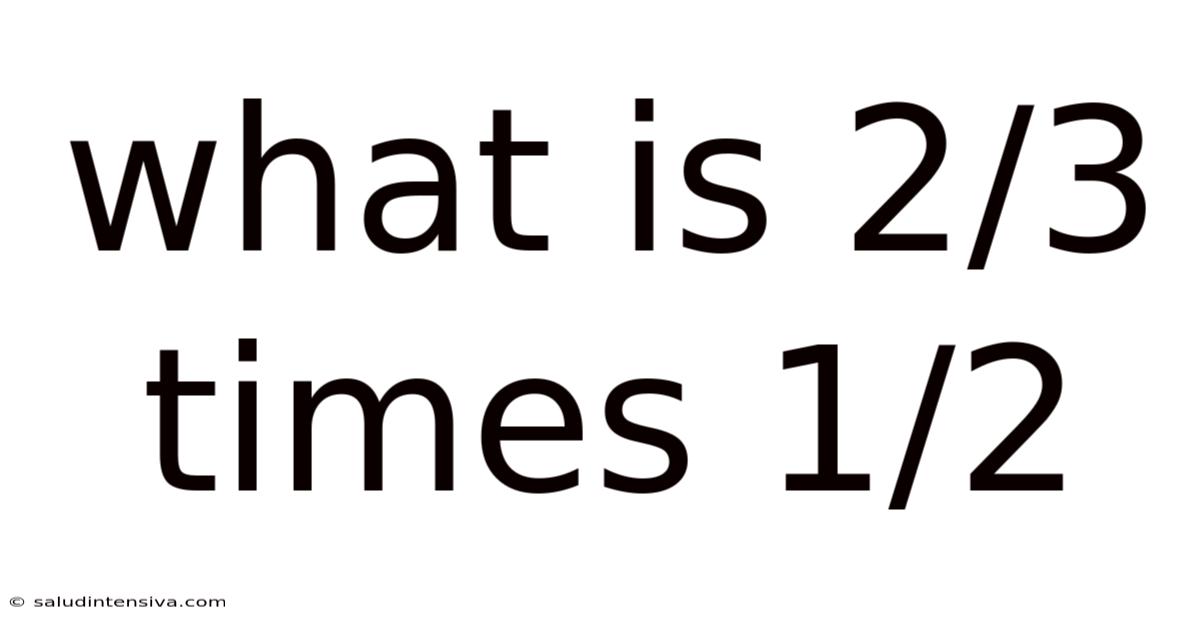
Table of Contents
What is 2/3 times 1/2? A Deep Dive into Fraction Multiplication
This article explores the seemingly simple question, "What is 2/3 times 1/2?", but delves far beyond the basic calculation to provide a comprehensive understanding of fraction multiplication, its applications, and its underlying mathematical principles. We'll cover the mechanics of the process, explore visual representations, connect it to real-world examples, and address common misconceptions. By the end, you'll not only know the answer to the initial question but possess a solid foundation in multiplying fractions.
Understanding Fractions: A Quick Refresher
Before tackling the multiplication problem, let's solidify our understanding of fractions. A fraction represents a part of a whole. It's expressed as a ratio of two numbers: the numerator (the top number) and the denominator (the bottom number). The denominator indicates how many equal parts the whole is divided into, while the numerator shows how many of those parts are being considered. For example, in the fraction 2/3, the denominator (3) means the whole is divided into three equal parts, and the numerator (2) indicates we're considering two of those parts.
Multiplying Fractions: The Method
Multiplying fractions is remarkably straightforward. It involves two simple steps:
- Multiply the numerators: Multiply the top numbers of the two fractions together.
- Multiply the denominators: Multiply the bottom numbers of the two fractions together.
The resulting fraction is the product of the original two fractions.
Let's apply this to our problem: 2/3 times 1/2.
- Multiply the numerators: 2 x 1 = 2
- Multiply the denominators: 3 x 2 = 6
Therefore, 2/3 times 1/2 = 2/6.
Simplifying Fractions: Finding the Lowest Terms
The fraction 2/6 is not in its simplest form. A fraction is in its simplest form, or lowest terms, when the greatest common divisor (GCD) of the numerator and denominator is 1. In other words, there's no number other than 1 that divides both the numerator and denominator evenly.
To simplify 2/6, we find the GCD of 2 and 6, which is 2. We then divide both the numerator and the denominator by the GCD:
2 ÷ 2 = 1 6 ÷ 2 = 3
So, the simplified form of 2/6 is 1/3. Therefore, the final answer to "What is 2/3 times 1/2?" is 1/3.
Visualizing Fraction Multiplication
Visual aids can greatly enhance understanding. Let's visualize 2/3 times 1/2 using a rectangle.
Imagine a rectangle representing the whole (1). Divide it into three equal vertical sections. Shading two of these sections represents 2/3.
Now, divide the same rectangle into two equal horizontal sections. Shading one of these sections represents 1/2.
The overlapping shaded area, where the 2/3 and 1/2 sections intersect, represents the product of 2/3 and 1/2. Observe that this overlapping area constitutes one-third of the entire rectangle. This visual demonstration confirms our calculated result of 1/3.
Real-World Applications of Fraction Multiplication
Fraction multiplication isn't confined to the realm of abstract mathematics; it has numerous real-world applications. Here are a few examples:
-
Cooking and Baking: Recipes often call for fractional amounts of ingredients. If a recipe requires 1/2 a cup of flour and you want to make only 2/3 of the recipe, you'd multiply 1/2 by 2/3 to determine the amount of flour needed (1/3 cup).
-
Construction and Measurement: In construction projects, precise measurements are critical. Calculating the area of a rectangular surface involving fractional dimensions necessitates fraction multiplication.
-
Finance and Budgeting: Dividing a budget or calculating portions of a total amount often involves fractions. For instance, if you want to allocate 2/3 of your savings towards a down payment and you have $1,500 saved, fraction multiplication will help you figure out the amount for the down payment.
-
Data Analysis: In statistics and data analysis, the manipulation and interpretation of datasets frequently involves fractions and requires multiplication of fractional values.
Understanding the "Of" Interpretation
The word "of" in mathematics often indicates multiplication. The problem "What is 2/3 of 1/2?" is mathematically identical to "What is 2/3 times 1/2?". Understanding this linguistic equivalence is crucial for interpreting word problems that involve fractions.
Addressing Common Misconceptions
Several common misconceptions surround fraction multiplication:
-
Adding instead of multiplying: A frequent error is to add the numerators and denominators rather than multiplying them. Remember, fraction multiplication involves multiplying, not adding.
-
Incorrect simplification: Failing to simplify the resulting fraction to its lowest terms is another common mistake. Always ensure your answer is reduced to the simplest form.
Extending the Concept: Multiplying More Than Two Fractions
The process of multiplying fractions can be extended to include more than two fractions. You simply multiply all the numerators together and all the denominators together. Remember to simplify the final result to its lowest terms.
Frequently Asked Questions (FAQ)
-
Q: Can I multiply fractions with different denominators? A: Absolutely! The method described above works for fractions with any denominators.
-
Q: What if one of the fractions is a whole number? A: Consider the whole number as a fraction with a denominator of 1. For example, 2 can be written as 2/1. Then, multiply as usual.
-
Q: What if the result is an improper fraction (numerator larger than the denominator)? A: It's perfectly acceptable to have an improper fraction as a result. You can either leave it as is or convert it into a mixed number (a whole number and a fraction).
Conclusion
While the initial question, "What is 2/3 times 1/2?", seems simple, it opens a door to a deeper understanding of fraction multiplication. Mastering this fundamental mathematical operation equips you with a powerful tool applicable across various fields, from cooking to finance. Remember the key steps: multiply the numerators, multiply the denominators, and always simplify to the lowest terms. By understanding the principles behind fraction multiplication and its visual representation, you can confidently tackle more complex fraction problems and appreciate its significance in the real world. The answer, 1/3, is only the beginning of a more profound journey into the fascinating world of fractions.
Latest Posts
Latest Posts
-
All The Multiples Of 16
Sep 19, 2025
-
11 000 Minutes To Hours
Sep 19, 2025
-
3 To The Tenth Power
Sep 19, 2025
-
5000 Sq Ft To Acres
Sep 19, 2025
-
Simplest Form For 8 12
Sep 19, 2025
Related Post
Thank you for visiting our website which covers about What Is 2/3 Times 1/2 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.