What Is 2 Times 2/3
saludintensiva
Sep 17, 2025 · 5 min read
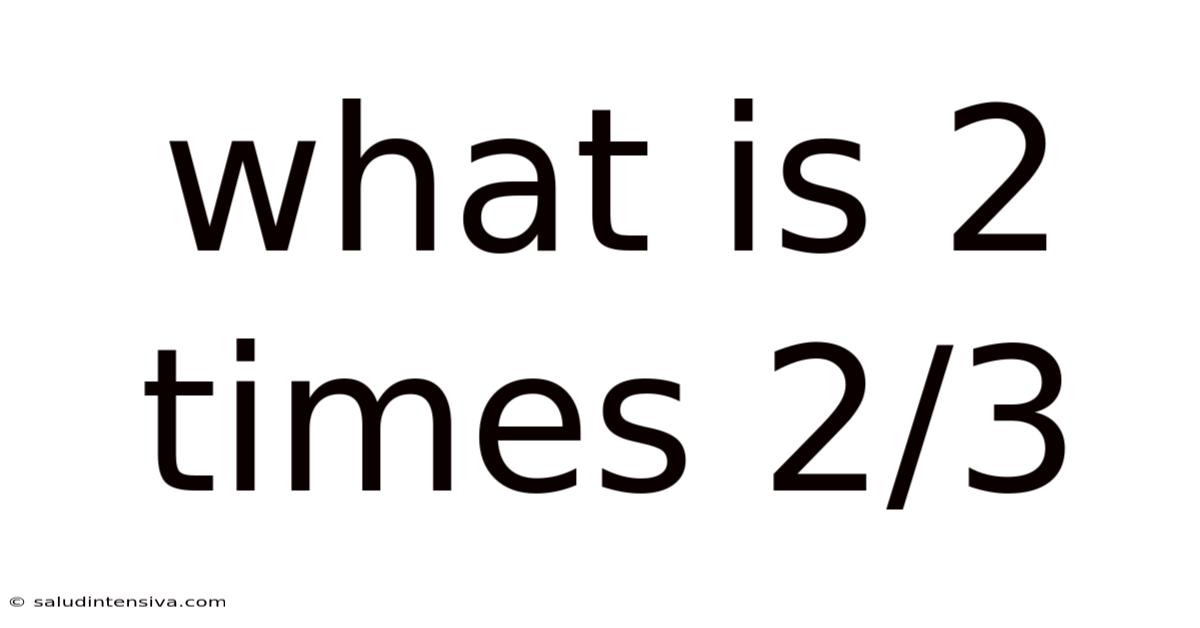
Table of Contents
What is 2 Times 2/3? A Deep Dive into Fractions and Multiplication
This article will explore the seemingly simple question, "What is 2 times 2/3?", but delve much deeper than just providing the answer. We'll unpack the fundamental concepts of fractions and multiplication, providing a solid understanding for learners of all levels. We’ll cover various methods for solving this problem and explore similar scenarios to build a strong foundation in arithmetic. By the end, you’ll not only know the answer but understand the why behind the calculation.
Introduction: Understanding Fractions and Multiplication
Before jumping into the calculation, let's review the basics. A fraction represents a part of a whole. It's expressed as a numerator (the top number) over a denominator (the bottom number). For example, in the fraction 2/3, the numerator is 2 and the denominator is 3. This means we have 2 out of 3 equal parts of something.
Multiplication, in its simplest form, is repeated addition. When we say 2 times 2/3, it means we're adding 2/3 to itself twice: 2/3 + 2/3. However, there are more efficient ways to calculate this, especially when dealing with more complex fractions.
Method 1: Direct Multiplication
The most straightforward method to calculate 2 times 2/3 is to treat the whole number 2 as a fraction with a denominator of 1 (2/1). Then, we multiply the numerators together and the denominators together:
(2/1) * (2/3) = (2 * 2) / (1 * 3) = 4/3
This gives us the answer as an improper fraction, where the numerator is larger than the denominator.
Method 2: Visual Representation
Visualizing the problem can be incredibly helpful, especially for beginners. Imagine a circle divided into three equal parts. 2/3 represents two of those parts. Multiplying by 2 means we have two sets of these two parts. This results in a total of four parts out of three, again represented as 4/3.
This visual method reinforces the concept of multiplication as repeated addition. We essentially added two sets of 2/3, resulting in 4/3.
Method 3: Converting to Mixed Number
The improper fraction 4/3 is perfectly acceptable, but it's often more convenient to express it as a mixed number. A mixed number combines a whole number and a proper fraction. To convert 4/3 to a mixed number, we perform a division:
4 ÷ 3 = 1 with a remainder of 1
This means 4/3 is equivalent to 1 and 1/3. So, 2 times 2/3 equals 1 and 1/3.
Understanding the Result: Improper Fractions and Mixed Numbers
The answer, whether expressed as 4/3 or 1 and 1/3, is perfectly correct. The choice depends on the context and the desired level of detail. Improper fractions are often preferred in further mathematical calculations, while mixed numbers are generally easier to understand intuitively. They both represent the same quantity.
Extending the Concept: Multiplying Fractions with Larger Numbers
Let's consider a more complex example: 5 times 3/4. Using the same principle as before:
(5/1) * (3/4) = (5 * 3) / (1 * 4) = 15/4
Converting this to a mixed number:
15 ÷ 4 = 3 with a remainder of 3
Therefore, 5 times 3/4 equals 3 and 3/4.
Simplifying Fractions Before Multiplication
Sometimes, we can simplify the calculation before even multiplying. If we notice common factors between the numerators and denominators, we can cancel them out. This makes the multiplication much easier.
For example: (6/8) * (4/3)
Notice that 6 and 3 share a common factor of 3, and 8 and 4 share a common factor of 4. We can simplify:
(6/8) * (4/3) = ( (6/3) / (8/4) ) = (2/2) * (4/3) = 1 *(4/3) = 4/3
Real-World Applications of Fraction Multiplication
The concept of multiplying fractions isn't confined to the classroom. It has numerous practical applications in daily life:
- Cooking: Doubling or tripling a recipe often involves multiplying fractions. If a recipe calls for 1/2 cup of flour, and you want to double it, you're multiplying 1/2 by 2.
- Construction: Calculating material quantities often requires fraction multiplication. If a project needs 2 and 1/2 meters of wood, and you need to build three such projects, you'll multiply 2 and 1/2 by 3.
- Finance: Calculating percentages or interest often involves fractions. Determining discounts, interest earned or paid often utilize these mathematical operations.
- Measurement: Converting between units (e.g., inches to feet) often involves multiplying by fractions.
Frequently Asked Questions (FAQ)
- What if I multiply a fraction by a decimal? Convert the decimal to a fraction first. For example, 0.5 is equivalent to 1/2.
- What if one of the numbers is negative? The rules of multiplication apply. A negative number multiplied by a positive number results in a negative number.
- How do I multiply more than two fractions? Simply multiply all the numerators together and all the denominators together. Simplify as needed.
- Why is it important to understand fractions and multiplication? Fractions and multiplication are foundational mathematical concepts essential for more advanced mathematical operations, problem-solving, and practical real-world applications.
Conclusion: Mastering Fractions and Multiplication
The calculation of 2 times 2/3, seemingly simple at first glance, opens up a world of understanding about fractions and multiplication. By mastering these fundamental concepts, you'll build a strong base for more complex mathematical problems. Remember to understand the logic behind the calculations, whether using direct multiplication, visual aids, or simplifying fractions. The ability to visualize and apply these principles will translate to a deeper and more meaningful understanding of mathematics, paving the way for success in more advanced studies and practical applications. Practice various problems, explore different methods, and soon you’ll confidently tackle any fraction multiplication problem.
Latest Posts
Latest Posts
-
How Many Minutes Is 120
Sep 17, 2025
-
Gcf Of 30 And 18
Sep 17, 2025
-
13000 Sq Ft In Acres
Sep 17, 2025
-
6 7 As A Decimal
Sep 17, 2025
-
12 100 As A Percentage
Sep 17, 2025
Related Post
Thank you for visiting our website which covers about What Is 2 Times 2/3 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.